Chủ đề này có 3 trả lời

[Zaraki]

Như vậy lời giải cho hai bài Tuần 2 tháng 5/2017 đã được đưa tại đây kèm theo đó là hai bài toán mới. Xin trích dẫn lại hai bài đó:

 

Bài 1. (Trần Quang Hùng) Cho đường tròn $(O)$ cố định với day $BC$ cố định và $A$ di chuyển bên trong $(O)$. Đường tròn $(K)$ tiếp xúc $CA,AB$ và tiếp xúc trong $(O)$. Một đường tròn khác $(O)$ qua $B,C$ tiếp xúc $(K)$ tại $P$. $J$ là tâm bàng tiếp góc $A$ của tam giác $ABC$. $H$ là hình chiếu của $A$ trên $BC$. $M,N$ là trung điểm $BC,AH$. $MN$ cắt $JP$ tại $Q$. Chứng minh rằng đường thẳng $AQ$ luôn đi qua một điểm cố định khi $A$ thay đổi.

 

Bài 2.  (Trần Quang Hùng, Trịnh Huy Vũ, Trần Quang Huy, Ngô Quang Dương) Cho tam giác $ABC$ có đường cao $AD,BE,CF$ đồng quy tại $H$. $O$ là tâm ngoại tiếp tam giác $ABC$. $P$ là một điểm nằm trên đường thẳng qua $Q$ song song $BC$. $Q$ là đẳng giác của $P$ trong tam giác $ABC$. $QB,QC$ cắt $EF$ tại $M,N$. Chứng minh rằng $A,M,H,N$ cùng thuộc một đường tròn. 

 

[ecchi123]

Lời giải bài 1 :

Gọi $(K)$ tiếp xúc với $(O)$ tại $Y$ . $I$ là tâm nội tam giác $ABC$.

Gọi $G$ là trung điểm cung $BC$ , $AG$ cắt $BC$ tại $T$ , ta có $M(GNAH)=-1$  nên  gọi $Q'$ là giao của $MN$ với $AG$ thì $(Q'GAT)=-1$. ta chứng minh $Q'$ trùng $Q$ , từ đó $AQ$ đy qua $G$ cố định

Thật vậy , tức là ta cần cm $X(PGAT)=-1$ với $X$ là giao của $PJ$ và $BC$

Gọi tiếp tuyến tại $P,Y$ cắt nhau tại $V$ thì xét trục đẳng phương $(K),(O),(PBC)$ thì $V$ thuộc $BC$ 

Suy ra $\frac{YB}{YC}=\sqrt{\frac{VB}{VC}}=\frac{PB}{PC}$ nên phân giác góc $BPC,BYC$ cắt nhau trên $BC$

Mặt khác , theo bài toán protassov thì $PJ$ là phân giác góc $BPC$ , từ đó suy ra $XY$ là phân giác góc $BYC$ 

Gọi $PL$ là phân giác ngoài $BPC$ suy ra $(LXBC)=-1$

$(K)$ cắt $AB,AC$ tại $E,F$ , $YE,YF$ cắt $(O)$ tại $Z,S$

ta so $ZS$ song song $EF$ nên $\frac{ZE}{ZY}=\frac{SY}{SY}=>\frac{ZE}{ZB}.\frac{ZB}{ZY}=\frac{SY}{SC}.\frac{SC}{SY}=>\frac{BE}{FC}=\frac{BY}{YC}=\frac{XB}{XC}$ suy ra $EF$ đy qua $L$ theo menelaus

Ta có $L$ đối cực với $XA$ qua $(K)$ nên $KL$ vuông góc với $XA$ tại $W$ , mặt khác $KP,KY$ là tiếp tuyến của $(XL)$

Chính vì vậy tứ giác $WPLY$ là tứ giác điều hòa  nên $X(WLPY)=-1=>X(PGAT)=-1$ , khi đó $XP$ đy qua $Q'$ , nên $Q$ trùng $Q'$ có dpcm

Bài viết đã được chỉnh sửa nội dung bởi ecchi123: 15-05-2017 - 21:08

[xuantrandong]

Lời giải bài $2$ của mình dài và chưa hay  

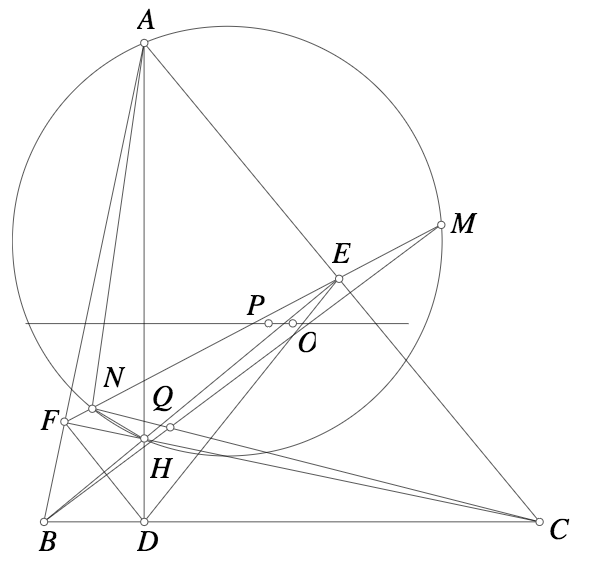
Bổ đề: Trên đường thẳng $d$, lấy các điểm $X,Y,E,F,M,N,I$ sao cho $(XYFE)=-1$, $I$ là trung điểm $EF$, $\overline{YM}.\overline{YN}=\overline{YX}.\overline{YI}$. Khi đó ta có $(MFIX)=(NEXI)$

Chứng minh bổ đề: Gọi tọa độ các điểm $X,E,F,M,N,I$ trên đường thẳng $d$ là $x,e,f,m,n,i$, chọn $Y$ làm gốc tọa độ.

Ta có (dễ thấy) :  $i=\frac{e+f}{2}$

                           $mn=x(\frac{e+f}{2})$

                           $x=\frac{2ef}{e+f}$

Biến đổi: $(MFIX)=(NEXI)\Leftrightarrow \overline{IM}.\overline{IN}.\overline{XE}.\overline{XF}=\overline{XM}.\overline{XN}.\overline{IE}.\overline{IF}\Leftrightarrow (m-\frac{e+f}{2})(n-\frac{e+f}{2})(x-e)(x-f)=-(x-m)(x-n)\frac{(e-f)^{2}}{4}\Leftrightarrow (\frac{(e+f)^{2}}{4}-\frac{(m+n)(e+f)}{2}+mn)=-(x^{2}-x(m+n)+mn)(\frac{(e-f)^{2}}{4})$

Thay  $mn=x(\frac{e+f}{2})$ vào ta có $\frac{e+f}{2}.(x-e)(x-f)=-x.\frac{(e-f)^{2}}{4}$, tiếp tục thay  $x=\frac{2ef}{e+f}$ vào ta được đẳng thức cuối cùng đúng, suy ra điều phải chứng minh.

Trở lại bài toán

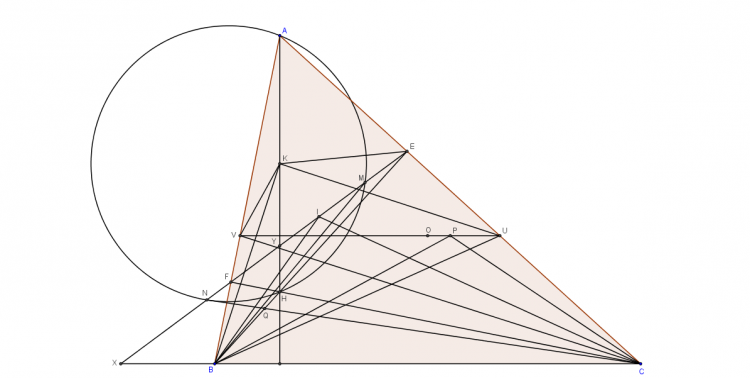
Gọi $K$ là trung điểm $AH$, $I$ là trung điểm $EF$, đường thẳng $EF$ giao $BC,AH$ tại $X,Y$, đường thẳng qua $K$ vuông góc $BK, CK$ giao $AC,AB$ tại $U,V$.

Dễ thấy $BKEU$ là tứ giác nội tiếp, nên $\angle KBU=\angle KEA=\angle KAE=\angle HBC\Rightarrow \angle KBE=\angle UBC$

Mà $\angle ABH=\angle OBC$ nên $\angle ABK=\angle OBU$, do đó $O,K$ đẳng giác trong $\Delta ABU$, nên $\angle OUB=\angle KUA=\angle KBE=\angle UBC$ do đó $OU$ song song $BC$. Mặt khác hai tam giác $BHA,BFE$ đồng dạng có $K,I$ là trung điểm của 2 cạnh tương ứng $HA,FE$ nên $\angle KBE=\angle IBA$ nên $\angle UBC=\angle IBA$

Chứng minh tương tự ta cũng được $\angle ICA=\angle VCB$

Do $OU,OV$ song song $BC$ nên $P,U,O,V$ thẳng hàng, nên $B(CUPV)=C(BUPV)$, xét phép đối xứng qua phân giác góc $B$ và phép chiếu xuyên tâm $B$ lên đường thẳng $EF$ thì $B(CUPV)=B(AIQC)=(FIMX)$, tương tự $C(BUPV)=C(ABQI)=(EXNI)$

Do đó $(FIMX)=(EXNI) \Rightarrow (MFIX) = (NEXI )$

Gọi đường tròn $(AMH)$ giao $EF$ tại $N'$ thì theo bổ đề ta có $(MFIX)=(N'EXI)$, vậy $N$ trùng $N'$

Dễ thấy $(XYFE)=-1$ do đó $(YXFE)=-1$, áp dụng hệ thức $Maclaurin$ thì $\overline{YI}.\overline{YX}=\overline{YE}.\overline{YF}$

Vậy $\overline{YM}.\overline{YN}=\overline{YX}.\overline{YI}=\overline{YH}.\overline{YA}$ nên $A,H,M,N$ cùng thuộc 1 đường tròn.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi xuantrandong: 15-05-2017 - 16:58

[manhtuan00]

Lời giải bài 1 : Gọi $G$ là tiếp điểm của $(K)$ với $(O)$. $X,Y,T$ lần lượt là giao của $AQ$ với $BC$, trung điểm cung lớn $BC$,  giao của tiếp tuyến tại $P$ với $BC$

Ta có $TP^2 = TB.TC$ nên $T$ nằm trên tiếp tuyến chung của $(K)$ và $(O)$. 

Áp dụng định lý Protassov cho $\triangle ABC$, đường tròn $(O)$ và đường tròn $(K)$, ta có $GI$ đi qua $Y$ do là phân giác . $GI$ cắt $BC$ tại $Z$

Áp dụng định lý Protassov cho $\triangle ABC$, đường tròn $(BPC)$ và đường tròn $(K)$, ta có $PJ$ là phân giác $\angle BPC$. Thật vậy, ta có $\frac{PB^2}{PC^2} = \frac{TB}{TC} = \frac{GB^2}{GC^2} = \frac{ZB^2}{ZC^2}$ nên $PZ$ là phân giác $\angle BPC$. Từ đây suy ra $P,Z,J$ thẳng hàng

Ta sẽ chứng minh $AQ$ đi qua $Y$. Thật vậy, ta giả sử $AY$ cắy $YP$ tại $Q$ thì ta cần chứng minh $MQ$ chia đôi $AH$. Gọi $L$ là giao điểm của $AJ$ với $BC$

Thật vậy ta cps : $M(AH,QY) = (AX,QY) =  Z(AX,QY) = Z(AL,JI) = (AL,JI) = -1$. Suy ra $MQ$ chia đôi $AH$. Vậy ta có điều cần chứng minh 

Bài viết đã được chỉnh sửa nội dung bởi manhtuan00: 21-05-2017 - 17:22