Chủ đề này có 37 trả lời

[ddang00]

Khi $ABCD$ không phải hình vuông em sẽ xử lí thế nào?

Vì khi $ABCD$ là hình vuông thì nó đã có diện tích lớn nhất rồi nên các trường hợp $ABCD$ không phải là hình vuông thì nó có diện tích bé hơn nên ta vẫn có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi ddang00: 30-05-2017 - 12:50

[IHateMath]

Vì khi $ABCD$ là hình vuông thì nó đã có diện tích lớn nhất rồi nên các trường hợp $ABCD$ không phải là hình vuông thì nó có diện tích bé hơn nên ta vẫn có điều phải chứng minh.

Hmm, lập luận như vậy chưa rõ ràng lắm. Ta chỉ biết là diện tích tứ giác $ABCD$ nhỏ hơn nhưng các tam giác bên trong nó thì sao? Làm sao để đảm bảo rằng diện tích của chúng cũng nhỏ hơn?

[NHoang1608]

b) Cho tứ giác $ABCD$ nội tiếp đường tròn $(O)$ bán kính bằng $R=4cm$ ($O$ nằm trong tứ giác $ABCD$). Xét 33 điểm phân biệt nằm trong tứ giác $ABCD$ sao cho không có 3 điểm nào thẳng hàng. Chứng minh rằng trong 33 điểm đó luôn tìm được 3 điểm là 3 đỉnh của một tam giác có diện tích nhỏ hơn $\frac{3\sqrt{3}}{4}cm^2$

Mình thấy cách giải của bạn ddang00 không hợp lí lắm. Như cách giải thích của anh IHateMath thì có vẻ cách của bạn chưa đúng hơn nữa nếu làm như vậy con số $\frac{3\sqrt{3}}{4}cm^{2}$ không có ý nghĩa cho lắm.

 

Cách giải của mình như sau:

 

Ta chia tứ giác $ABCD$ thành $16$ tứ giác nội tiếp trong đường tròn bán kính $1$ như hình trên bằng cách lấy các trung điểm của cạnh tứ giác $ABCD$ và làm thế 1 lần nữa với $4$ tứ giác vừa được chia ra.

Theo nguyên lí $Dirichlet$ thì tồn tại $3$ điểm trong $33$ đã cho cùng thuộc $1$ tứ giác trong $16$ tứ giác vừa được chia ra

$3$ điểm này thuộc hình tròn bán kính bằng $1$. Ta sẽ chứng minh $3$ điểm này là $3$ điểm cần tìm.

Gọi $3$ điểm này là $E,F,G$

Xảy ra $3$ trường hợp:

TH1 3 điểm này không nằm trên đường tròn. Vẽ $EF$ cắt $(I)$ tại $M$. Đường thẳng $EG$ cắt $(I)$ tại $N,K$.

Dễ thấy $S_{EFG}< S_{MNK}$. Mà ta lại có diện tích của 1 tam giác bất kì nội tiếp đường tròn không quá diện tích tam giác đều nội tiếp đường tròn đó. Dễ tính được diện tích tam giác đều nội tiếp đường tròn bán kính $1$ là $\frac{3\sqrt{3}}{4}cm^{2}$

Suy ra $S_{EFG}< S_{MNK}\leq \frac{3\sqrt{3}}{4}cm^{2} $

TH2 Tồn tại ít nhất $1$ điểm trong $3$ điểm nằm trên đường tròn.

Vẽ như TH1 và giải như TH1

TH3 3 điểm này nằm trên đường tròn. Giải như TH1 thì $S_{EFG}\leq  \frac{3\sqrt{3}}{4}cm^{2}$

 

Như vậy ta có điều phải chứng minh

[ddang00]

TH3 3 điểm này nằm trên đường tròn. Giải như TH1 thì $S_{EFG}\leq  \frac{3\sqrt{3}}{4}cm^{2}$

 

Bạn thử xem lại đề bài và trường hợp 3 xem

Đề yêu cầu là Chứng minh rằng trong 33 điểm đó luôn tìm được 3 điểm là 3 đỉnh của một tam giác có diện tích nhỏ hơn  $\frac{3\sqrt{3}}{4}cm^2$ chứ không phải nhỏ hơn hoặc bằng bạn nhé!

Bài viết đã được chỉnh sửa nội dung bởi ddang00: 30-05-2017 - 17:44

[Minhnksc]

Mình thấy cách giải của bạn ddang00 không hợp lí lắm. Như cách giải thích của anh IHateMath thì có vẻ cách của bạn chưa đúng hơn nữa nếu làm như vậy con số $\frac{3\sqrt{3}}{4}cm^{2}$ không có ý nghĩa cho lắm.

 

Cách giải của mình như sau:

 

ScreenHunter_35 May. 30 14.25.jpg

Ta chia tứ giác $ABCD$ thành $16$ tứ giác nội tiếp trong đường tròn bán kính $1$ như hình trên bằng cách lấy các trung điểm của cạnh tứ giác $ABCD$ và làm thế 1 lần nữa với $4$ tứ giác vừa được chia ra.

Theo nguyên lí $Dirichlet$ thì tồn tại $3$ điểm trong $33$ đã cho cùng thuộc $1$ tứ giác trong $16$ tứ giác vừa được chia ra

$3$ điểm này thuộc hình tròn bán kính bằng $1$. Ta sẽ chứng minh $3$ điểm này là $3$ điểm cần tìm.

ScreenHunter_36 May. 30 14.38.jpg

Gọi $3$ điểm này là $E,F,G$

Xảy ra $3$ trường hợp:

TH1 3 điểm này không nằm trên đường tròn. Vẽ $EF$ cắt $(I)$ tại $M$. Đường thẳng $EG$ cắt $(I)$ tại $N,K$.

Dễ thấy $S_{EFG}< S_{MNK}$. Mà ta lại có diện tích của 1 tam giác bất kì nội tiếp đường tròn không quá diện tích tam giác đều nội tiếp đường tròn đó. Dễ tính được diện tích tam giác đều nội tiếp đường tròn bán kính $1$ là $\frac{3\sqrt{3}}{4}cm^{2}$

Suy ra $S_{EFG}< S_{MNK}\leq \frac{3\sqrt{3}}{4}cm^{2} $

TH2 Tồn tại ít nhất $1$ điểm trong $3$ điểm nằm trên đường tròn.

Vẽ như TH1 và giải như TH1

TH3 3 điểm này nằm trên đường tròn. Giải như TH1 thì $S_{EFG}\leq  \frac{3\sqrt{3}}{4}cm^{2}$

 

Như vậy ta có điều phải chứng minh

 

Bạn thử xem lại đề bài và trường hợp 3 xem

Đề yêu cầu là Chứng minh rằng trong 33 điểm đó luôn tìm được 3 điểm là 3 đỉnh của một tam giác có diện tích nhỏ hơn  $\frac{3\sqrt{3}}{4}cm^2$ chứ không phải nhỏ hơn hoặc bằng bạn nhé!

Mình là nên tính số tam giác đôi một không có điểm trong chung nhiều nhất có thể tạo bởi 33 điểm trên; giả sử là $n$; thì khi này tồn tại một tam giác có diện tích nhỏ hơn $\frac{S_{ABCD}}{n}$; mà $S_{ABCD}\leq 32cm^2$ nên ta chỉ cần chứng minh $\frac{32}{n}<\frac{3\sqrt{3}}{4}$ là xong. Tuy nhiên là mình khá băn khoăn về con số $\frac{3\sqrt{3}}{4}$

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 30-05-2017 - 18:19

[ddang00]

Mình là nên tính số tam giác đôi một không có điểm trong chung nhiều nhất có thể tạo bởi 33 điểm trên; giả sử là $n$; thì khi này tồn tại một tam giác có diện tích nhỏ hơn $\frac{S_{ABCD}}{n}$; mà $S_{ABCD}\leq 32cm^2$ nên ta chỉ cần chứng minh $\frac{32}{n}<\frac{3\sqrt{3}}{4}$ là xong. Tuy nhiên là mình khá băn khoăn về con số $\frac{3\sqrt{3}}{4}$

Nếu thế thì mình nghĩ cách của bạn na ná của mình rồi, mình cũng băn khoăn con số $\frac{3\sqrt{3}}{4}$ nhưng theo mình nghĩ đề yêu cầu bé hơn nên nó cũng có thể là để đánh lạc hướng suy nghĩ hoặc phụ trợ cho một giá trị nhỏ hơn thôi!

Nhưng vấn đề là theo cách của $NHoang1608$ thì con số đó lại có tác dụng.

[Minhnksc]

Mình cũng nên nói thêm là câu 1a rất dễ nhầm lẫn vì đề bài yêu cầu tìm số tự nhiên $x$ chứ không phải là tìm $x$; như vậy đáp án của bác $quangantoan$ trở nên vô nghĩa.

Hơn nữa; mình nghĩ là đề này chưa thực sự để lại cho mình nhiều ấn tượng; nhất là câu hình; câu hệ phương trình với phương trình (chắc cũng phải đề cập thêm cả câu số học ) so với mấy năm trước thì năm nay nhạt toẹt.

[quochoangkim]

Nếu mà như thế thì cx dễ
Đpcm $\Leftrightarrow K$ nằm trên đường tròn tâm $(O)$ bán kính $BD=BK$
$\Leftrightarrow BD=BH$
$\Leftrightarrow BI.BC=BD^{2}=BH^{2}$
$\Leftrightarrow BH=\frac{1}{2} BC$
(Đúng)
$\Rightarrow Q.E.D$

Đường tròn tâm (B) nhé !

[HoangKhanh2002]

Còn đây là lời giải bài Tổ của mình. Sao các bạn cứ nghiêm trọng nó lên vậy

Ta dễ dàng tính được $S_{ht}\approx 50,27(cm^2)$

Lấy một điểm S bất kì trong tứ giác ABCD, khi đó tứ giác ABCD được chia thành 4 tam giác. Lại lấy điểm S' trong một tam giác bất kì, cứ tiếp tục như vậy. Nhận thấy, số tam giác tạo thành là: $3+32.2=67$

Mà: $S_{ABCD}<S_{ht}<50,27$ nên tồn tại một trong $67$ tam giác có diện tích: $<\dfrac{50,27}{67}<\dfrac{3\sqrt{3}}{4}$

Ta có ngay đpcm

[Minhnksc]

Còn đây là lời giải bài Tổ của mình. Sao các bạn cứ nghiêm trọng nó lên vậy

lhp to.png

Ta dễ dàng tính được $S_{ht}\approx 50,27(cm^2)$

Lấy một điểm S bất kì trong tứ giác ABCD, khi đó tứ giác ABCD được chia thành 4 tam giác. Lại lấy điểm S' trong một tam giác bất kì, cứ tiếp tục như vậy. Nhận thấy, số tam giác tạo thành là: $3+32.2=67$

Mà: $S_{ABCD}<S_{ht}<50,27$ nên tồn tại một trong $67$ tam giác có diện tích: $<\dfrac{50,27}{67}<\dfrac{3\sqrt{3}}{4}$

Ta có ngay đpcm

Lời giải của bạn chưa đúng vì các tam giác chỉ được phép tạo thành từ 33 điểm đã cho chứ không được tạo thành bởi 4 điểm $A;B;C;D$; còn 67 tam giác như bạn đã nêu ở trên thì đã có các tam giác mà đỉnh của chúng không nằm trong số 33 điểm đã cho

[HoangKhanh2002]

Lời giải của bạn chưa đúng vì các tam giác chỉ được phép tạo thành từ 33 điểm đã cho chứ không được tạo thành bởi 4 điểm $A;B;C;D$; còn 67 tam giác như bạn đã nêu ở trên thì đã có các tam giác mà đỉnh của chúng không nằm trong số 33 điểm đã cho

Theo mình nghĩ lời giải của mình không sai, đề bài yêu cầu chứng minh tồn tại, nên sẽ có ít nhất một tam giác tạo thành không cần sử dụng đến 4 điểm $A, B, C, D$. Mà điều này thì hiển nhiên.  Còn nếu mình sai thì các bạn cứ nói

[Minhnksc]

Theo mình nghĩ lời giải của mình không sai, đề bài yêu cầu chứng minh tồn tại, nên sẽ có ít nhất một tam giác tạo thành không cần sử dụng đến 4 điểm $A, B, C, D$. Mà điều này thì hiển nhiên.  Còn nếu mình sai thì các bạn cứ nói

Ý mình là trong lời giải của bạn có dòng:

 

Mà: $S_{ABCD}<S_{ht}<50,27$ nên tồn tại một trong $67$ tam giác có diện tích: $<\dfrac{50,27}{67}<\dfrac{3\sqrt{3}}{4}$

 

Nếu cái tam giác mà bạn nói đến có một đỉnh là một trong số các đỉnh $A;B;C;D$ thì sao? Mình băn khoăn chỗ đó

Bài viết đã được chỉnh sửa nội dung bởi Minhnksc: 31-05-2017 - 16:55

[ddang00]

Mà: $S_{ABCD}<S_{ht}<50,27$ nên tồn tại một trong $67$ tam giác có diện tích: $<\dfrac{50,27}{67}<\dfrac{3\sqrt{3}}{4}$

Ta có ngay đpcm

Bạn thử nghĩ lại xem vì ta dễ dàng chứng minh được $S_{ABCD}\leq32$ rồi nên theo cách của bạn thì mỗi tam giác có diện tích $<\dfrac{32}{67}<\dfrac{1}{2}<\frac{\frac{3\sqrt{3}}{4}}{2}$ đó. Khi đó kết quả sẽ cách cả một khoảng dài như thế à!

Bài viết đã được chỉnh sửa nội dung bởi ddang00: 31-05-2017 - 17:31

[xuanhoan23112002]

moi nguoi hom nay co ket qua LHP day hoi hop qua hi vong do co vu cho minh nhe

[xuanhoan23112002]

minh nghi bai to hop cac ban can chung minh co 1 tam giac co 3 dinh la 3 trong cac diem da cho va canh cua tam giac nho hon 1 thi dung cong thuc tinh dien tich bang sin60 se ra ngay

[xuanhoan23112002]

Mình thấy cách giải của bạn ddang00 không hợp lí lắm. Như cách giải thích của anh IHateMath thì có vẻ cách của bạn chưa đúng hơn nữa nếu làm như vậy con số $\frac{3\sqrt{3}}{4}cm^{2}$ không có ý nghĩa cho lắm.

 

Cách giải của mình như sau:

 

ScreenHunter_35 May. 30 14.25.jpg

Ta chia tứ giác $ABCD$ thành $16$ tứ giác nội tiếp trong đường tròn bán kính $1$ như hình trên bằng cách lấy các trung điểm của cạnh tứ giác $ABCD$ và làm thế 1 lần nữa với $4$ tứ giác vừa được chia ra.

Theo nguyên lí $Dirichlet$ thì tồn tại $3$ điểm trong $33$ đã cho cùng thuộc $1$ tứ giác trong $16$ tứ giác vừa được chia ra

$3$ điểm này thuộc hình tròn bán kính bằng $1$. Ta sẽ chứng minh $3$ điểm này là $3$ điểm cần tìm.

ScreenHunter_36 May. 30 14.38.jpg

Gọi $3$ điểm này là $E,F,G$

Xảy ra $3$ trường hợp:

TH1 3 điểm này không nằm trên đường tròn. Vẽ $EF$ cắt $(I)$ tại $M$. Đường thẳng $EG$ cắt $(I)$ tại $N,K$.

Dễ thấy $S_{EFG}< S_{MNK}$. Mà ta lại có diện tích của 1 tam giác bất kì nội tiếp đường tròn không quá diện tích tam giác đều nội tiếp đường tròn đó. Dễ tính được diện tích tam giác đều nội tiếp đường tròn bán kính $1$ là $\frac{3\sqrt{3}}{4}cm^{2}$

Suy ra $S_{EFG}< S_{MNK}\leq \frac{3\sqrt{3}}{4}cm^{2} $

TH2 Tồn tại ít nhất $1$ điểm trong $3$ điểm nằm trên đường tròn.

Vẽ như TH1 và giải như TH1

TH3 3 điểm này nằm trên đường tròn. Giải như TH1 thì $S_{EFG}\leq  \frac{3\sqrt{3}}{4}cm^{2}$

 

Như vậy ta có điều phải chứng minh

sao ban biet 16 tu giac deu noi tiep

[Minhnksc]

sao ban biet 16 tu giac deu noi tiep

Các tứ giác trên đều có hai góc đối bằng $90^0$ nên chúng đều nội tiếp

Spoiler

bạn nên đánh chữ có dấu và bạn cũng không nên spam ở topic này nhé

[Nguyen Xuan Hieu]

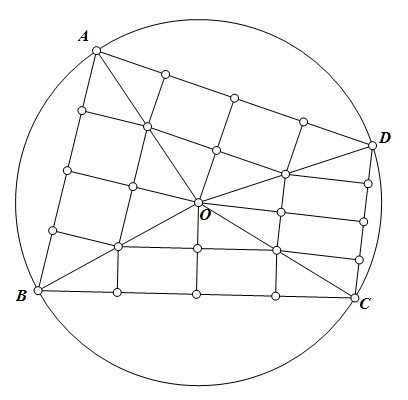
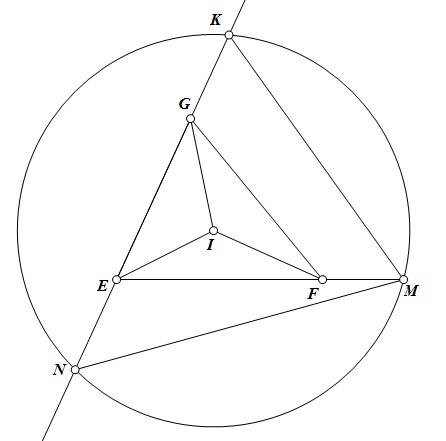
Bài 3:

a) $\widehat{DIC}=\widehat{BOA}=\widehat{BEC}$

$\Rightarrow Q.E.D$

 

 

b) Hình như phải là $\widehat{DHB}=\frac{1}{2}\widehat{DHE}$

Ta có:$AD.AE=AB^{2}=AH.AO$

Do đó,$DHOE$ nội tiếp

$\Rightarrow \widehat{DHA}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\\\Rightarrow \widehat{DHB}=\frac{1}{2}\widehat{DHE}\Rightarrow Q.E.D$

 

 

c) Tính chất tứ giác điều hòa

Đề đúng rồi đấy.

Gọi $J$ là trung điểm của $DE$.

Khi đó dễ thấy $OJ \perp AE$ nên $5$ điểm: $A,B,J,O,C,A$ cùng thuộc một đường tròn.

Khi đó tứ giác $JBAC$ nội tiếp $\Rightarrow \widehat{DJC}=\widehat{AJC}=\widehat{ABC}=\widehat{BIF}=\widehat{DIC}$.

Do đó tứ giác $DIJC$ nội tiếp $\Rightarrow \widehat{DJC}=\widehat{DCI}=\widehat{DCB}=\widehat{DEB}$.

Do đó $IJ//EF$ mà $J$ là trung điểm của $DE \Rightarrow I$ là trung điểm của $DF$.

Mặt khác $I$ cũng là trung điểm của $BH$ nên $BDHF$ là hình bình hành.

Lại có:$AD.AE=AB^2=AC^2=AH.AO$ do đó,$DHOE$ nội tiếp

$\Rightarrow \widehat{DHA}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\\\Rightarrow \widehat{DHB}=\frac{1}{2}\widehat{DHE}$

Từ điều trên dễ thấy $\widehat{EBH}=\widehat{EHB}$ nên tam giác $EBH$ cân mà $I$ là trung điểm $BH$ nên $KI \perp CI$ mà $EFIC$ nội tiếp nên $CF \perp FE$.

Mà $H$ là trung điểm $BC$.

Nên $\widehat{HFC}=\widehat{HCF}$ hay $\widehat{BHF}=2\widehat{HCF}$.

Mà $\widehat{DBC}=\widehat{BHF}(BD//FH) \Rightarrow \widehat{DBC}=2\widehat{HCF}$.

Dễ dàng chứng minh tứ giác $FHCK$ nt ($\widehat{BHF}=\widehat{DBC}=\widehat{DKC}$) nên $\widehat{HCF}=\widehat{FKH}=\widehat{DKH}$.

Do đó $\widehat{BHF}=2\widehat{HCF}=2\widehat{DKH}$
P/s: Cho hỏi sao up ảnh lên diễn đàn được vậy? Mình chụp màn hình rồi crt +v thì nó bảo là không hỗ trợ định dạng
 

Bài viết đã được chỉnh sửa nội dung bởi Nguyen Xuan Hieu: 10-06-2017 - 15:35