Đề thi tuyển sinh THPT chuyên Bà Rịa - Vũng Tàu 2017-2018

Đề thi tuyển sinh THPT chuyên Bà Rịa - Vũng Tàu 2017-2018
#1
 Đã gửi 31-05-2017 - 17:13
Đã gửi 31-05-2017 - 17:13

- Nike Adidas yêu thích
#2
 Đã gửi 31-05-2017 - 19:54
Đã gửi 31-05-2017 - 19:54

Câu 3
căn(2(x^2+y^2)) >= x+y
=> (1/x+1/y).căn(2(x^2+y^2)) >= ((x+y)^2)/xy = ((x^2+y^2)/xy) + 2
P>= 4xy/(x^2+y^2) + ((x^2+y^2)/xy) + 2 - 3xy/(x^2+y^2)
>= 2.2 + 2 - (3.(x^2+y^2)/2)/(x^2+y^2) = 9/2
Đẳng thức xảy ra khi và chỉ khi x = y.
Done!
- Nike Adidas yêu thích
#3
 Đã gửi 31-05-2017 - 19:57
Đã gửi 31-05-2017 - 19:57

#4
 Đã gửi 31-05-2017 - 20:11
Đã gửi 31-05-2017 - 20:11

Do $ \displaystyle P\left( x \right)>0\Rightarrow \left\{ \begin{array}{l}{{b}^{2}}-4ac<0\Rightarrow b\in \left[ {-2\sqrt{{ac}};2\sqrt{{ac}}} \right]\\a>0\\c>0\end{array} \right.$
Khi đó cần chứng minh $ \displaystyle 5a+b+3c>a-b+c\Leftrightarrow 4a+2b+2c>0\Leftrightarrow 2a+b+c>0$
Theo $AM-GM$ ta có: $ \displaystyle a+c\ge 2\sqrt{{ac}}\ge b\Rightarrow 2a+b+c>0$
Vậy ta có đpcm
- hoicmvsao, Nike Adidas, Tea Coffee và 1 người khác yêu thích
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#5
 Đã gửi 31-05-2017 - 20:54
Đã gửi 31-05-2017 - 20:54

Câu 1b: ĐK: $x\geq 3$
Phương trình $\Leftrightarrow (x-2)^2(x-12)=0$
c)Phương trình 1 $\Leftrightarrow (x-y)(x+2y)=0$ rồi thay lần lượt $x=y;x=-2y$ vào pt 2
Câu 3: Ta có: $P\geq \frac{xy}{x^2+y^2}+\frac{x^2+y^2}{xy}+2=\frac{x^2+y^2}{4xy}+\frac{xy}{x^2+y^2}+\frac{3(x^2+y^2)}{4xy}+2\geq 1+\frac{7}{2}=\frac{9}{2}$
- Nike Adidas, quangantoan, hoangtuyeuai2809 và 2 người khác yêu thích
Chấp nhận giới hạn của bản thân, nhưng đừng bao giờ bỏ cuộc
#6
 Đã gửi 01-06-2017 - 14:55
Đã gửi 01-06-2017 - 14:55

hai bài hình khó khủng khiếp
" Khi ta đã quyết định con đường cho mình, kẻ được nói ta ngu ngốc chỉ có bản thân ta mà thôi. " _ Rononoa Zoro.
#7
 Đã gửi 01-06-2017 - 17:03
Đã gửi 01-06-2017 - 17:03

#8
 Đã gửi 02-06-2017 - 01:50
Đã gửi 02-06-2017 - 01:50

Bài hình câu 5 dùng hai tam giác có chung đường cao thì tỉ lệ diện tích là tỉ lệ đáy nhé
- Nike Adidas và hoangtuyeuai2809 thích
#9
 Đã gửi 02-06-2017 - 21:28
Đã gửi 02-06-2017 - 21:28

câu 5 sử dụng bổ đề:
cho tam giac ABC trung tuyến AM . Một đường thẳng bất kỳ cắt đoạn AB,AM,AC tại D,E,F. K
- hoangtuyeuai2809 yêu thích
" Khi ta đã quyết định con đường cho mình, kẻ được nói ta ngu ngốc chỉ có bản thân ta mà thôi. " _ Rononoa Zoro.
#10
 Đã gửi 02-06-2017 - 21:30
Đã gửi 02-06-2017 - 21:30

Khi đó ta có $\frac{BD}{DA}+\frac{CF}{FA}=2\frac{ME}{EA }$
- hoangtuyeuai2809 yêu thích
" Khi ta đã quyết định con đường cho mình, kẻ được nói ta ngu ngốc chỉ có bản thân ta mà thôi. " _ Rononoa Zoro.
#11
 Đã gửi 02-06-2017 - 22:22
Đã gửi 02-06-2017 - 22:22

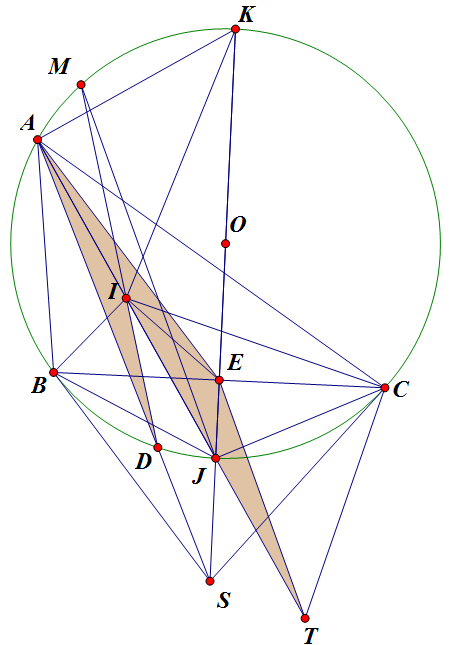
Câu a,b dễ chém câu c:
Gọi $T$ là tâm đường tròn bàng tiếp góc $A$ .
Dễ dàng thấy $J$ là trung điểm $IT$.
$\bigtriangleup ATC \sim BAJ (g-g )$ vì $\angle BAI = \angle IAC; \angle ACT = 90 + \angle ACI = \angle AIB$ (biến đổi góc )
Suy ra : $AI. AT =AB.AC (1)$
Lại chứng minh được: $ \bigtriangleup AEC \sim \bigtriangleup ABD $
Suy ra $AB.AC = AE.AD (2)$
Từ $(1)$ và $(2)$ suy ra $AI.AT = AE.AD$ suy ra $\bigtriangleup AID \sim \bigtriangleup AET (c-g-c)$
Suy ra: $\angle ATE =\angle ADI =\angle AJM $ Suy ra $JM // ET$ mà $J$ là trung điểm $IT$
Vậy suy ra $JM$ đi qua trung điểm $IE$.
P/s: Bài này khó thật.
Bài viết đã được chỉnh sửa nội dung bởi Nguyenphuctang: 02-06-2017 - 22:23
#12
 Đã gửi 03-06-2017 - 08:00
Đã gửi 03-06-2017 - 08:00

Câu 3
căn(2(x^2+y^2)) >= x+y
=> (1/x+1/y).căn(2(x^2+y^2)) >= ((x+y)^2)/xy = ((x^2+y^2)/xy) + 2
P>= 4xy/(x^2+y^2) + ((x^2+y^2)/xy) + 2 - 3xy/(x^2+y^2)
>= 2.2 + 2 - (3.(x^2+y^2)/2)/(x^2+y^2) = 9/2
Đẳng thức xảy ra khi và chỉ khi x = y.
Done!
#13
 Đã gửi 03-06-2017 - 16:27
Đã gửi 03-06-2017 - 16:27

bài hình khó
Bài viết đã được chỉnh sửa nội dung bởi kokothoat: 03-06-2017 - 16:31
#14
 Đã gửi 18-06-2017 - 22:08
Đã gửi 18-06-2017 - 22:08

Câu a,b dễ chém câu c:
Gọi $T$ là tâm đường tròn bàng tiếp góc $A$ .
Dễ dàng thấy $J$ là trung điểm $IT$.
$\bigtriangleup ATC \sim BAJ (g-g )$ vì $\angle BAI = \angle IAC; \angle ACT = 90 + \angle ACI = \angle AIB$ (biến đổi góc )
Suy ra : $AI. AT =AB.AC (1)$
Lại chứng minh được: $ \bigtriangleup AEC \sim \bigtriangleup ABD $
Suy ra $AB.AC = AE.AD (2)$
Từ $(1)$ và $(2)$ suy ra $AI.AT = AE.AD$ suy ra $\bigtriangleup AID \sim \bigtriangleup AET (c-g-c)$
Suy ra: $\angle ATE =\angle ADI =\angle AJM $ Suy ra $JM // ET$ mà $J$ là trung điểm $IT$
Vậy suy ra $JM$ đi qua trung điểm $IE$.
P/s: Bài này khó thật.
anh cho em hỏi tam giác AEC đồng dạng tam giác ABD theo trường hợp nào? Anh có thể giải thích rõ giúp em được không ạ? Em cám ơn ạ!
#15
 Đã gửi 19-06-2017 - 15:09
Đã gửi 19-06-2017 - 15:09

anh cho em hỏi tam giác AEC đồng dạng tam giác ABD theo trường hợp nào? Anh có thể giải thích rõ giúp em được không ạ? Em cám ơn ạ!
$AS$ là đường đối trung $\Rightarrow \angle BAS = \angle EAC; \angle ADB = \angle ECA \Rightarrow \bigtriangleup BAD \sim \bigtriangleup EAC (g.g)$
Đường đối trung có thể chứng minh bằng kiến thức $\text{THCS}$:
 ___ng_th_ng_symedian.pdf 148.67K
622 Số lần tải
___ng_th_ng_symedian.pdf 148.67K
622 Số lần tải
#16
 Đã gửi 20-06-2017 - 00:21
Đã gửi 20-06-2017 - 00:21

$AS$ là đường đối trung $\Rightarrow \angle BAS = \angle EAC; \angle ADB = \angle ECA \Rightarrow \bigtriangleup BAD \sim \bigtriangleup EAC (g.g)$
Đường đối trung có thể chứng minh bằng kiến thức $\text{THCS}$:
Em cám ơn. Em hiểu rùi ạ
#17
 Đã gửi 03-07-2017 - 15:48
Đã gửi 03-07-2017 - 15:48

Câu 2.2:
Với $p=2\Rightarrow A= n^{4}+4n=k^{2} (k \in N)$
Xét $n\geq 0$ thì ta có $(n^{2})^{2}\leq {n^{4}+4n}<(n^{2}+1)^{2}$, dễ dàng tìm được $n=0$ thỏa mãn.
Xét $n< -2$ thì ta có $(n^{2}-1)^{2}<A<n^{4}$, không tìm ra $n$ thỏa mãn.
Xét $n=-1$ thấy không thỏa mãn, $n=-2$ không thỏa mãn.
Với $p>2$, ta có $A=n^{4}+4n^{p+1}=k^{2} \Leftrightarrow n^{2}+4n^{p-1}=\frac{k^{2}}{n^{2}}= m^{2}(m \in N)\Leftrightarrow (m-n)(m+n)= 4n^{p-1}$, giả sử $n$ không chia hết cho $p$, khi đó theo định lý Fermat nhỏ ta có: $4n^{p-1}\equiv 4 ($mod $p)$, đến đây suy ra
$(m-n)(m+n)\equiv 4($mod $p)$ ,đến đây xét ước, suy ra $n\vdots p$, nên loại :v
Vậy $n=0$ là nghiệm nguyên dương cần tìm.
Bài viết đã được chỉnh sửa nội dung bởi khoaitokhonglochetdoi: 03-07-2017 - 15:48
- NHoang1608, Hoang Dinh Nhat và ThinhThinh123 thích
#18
 Đã gửi 04-07-2017 - 20:57
Đã gửi 04-07-2017 - 20:57

Câu 2.2:
Với $p=2\Rightarrow A= n^{4}+4n=k^{2} (k \in N)$
Xét $n\geq 0$ thì ta có $(n^{2})^{2}\leq {n^{4}+4n}<(n^{2}+1)^{2}$, dễ dàng tìm được $n=0$ thỏa mãn.
Xét $n< -2$ thì ta có $(n^{2}-1)^{2}<A<n^{4}$, không tìm ra $n$ thỏa mãn.
Xét $n=-1$ thấy không thỏa mãn, $n=-2$ không thỏa mãn.
Với $p>2$, ta có $A=n^{4}+4n^{p+1}=k^{2} \Leftrightarrow n^{2}+4n^{p-1}=\frac{k^{2}}{n^{2}}= m^{2}(m \in N)\Leftrightarrow (m-n)(m+n)= 4n^{p-1}$, giả sử $n$ không chia hết cho $p$, khi đó theo định lý Fermat nhỏ ta có: $4n^{p-1}\equiv 4 ($mod $p)$, đến đây suy ra
$(m-n)(m+n)\equiv 4($mod $p)$ ,đến đây xét ước, suy ra $n\vdots p$, nên loại :v
Vậy $n=0$ là nghiệm nguyên dương cần tìm.
Với p > 2 còn trường hợp n chia hết p thì thế nào bạn?
#19
 Đã gửi 05-07-2017 - 08:53
Đã gửi 05-07-2017 - 08:53

Khi đó ta có $\frac{BD}{DA}+\frac{CF}{FA}=2\frac{ME}{EA }$
chứng minh bổ đề này như nào bạn
#20
 Đã gửi 05-07-2017 - 09:51
Đã gửi 05-07-2017 - 09:51

Với p > 2 còn trường hợp n chia hết p thì thế nào bạn?
Đây mình làm lại nhé, thông cảm ![]()
Với $p=2$, khi đó bạn tìm được $x=0$ thỏa mãn
Với $p>2$
khi đó $A= (n)^{4}+4(n)^{p+1}=t^{2}\Leftrightarrow 1+4(n)^{p-3}=\frac{t^{2}}{(n)^{4}}=(\frac{t}{n^{2}})^{2}$
Vì VT là một số tự nhiên (do $p>2$) nên VP cũng là một số tự nhiên, nên $(\frac{t}{n^{2}})^{2}$ là số chính phương, lại có $p>2$ nên $p$ là số lẻ(nguyên tố mà), nên $4(n)^{p-3}$ là một số chính phương, đến đây có dạng $1+x^{2}=y^{2}$, chắc dễ ![]()
- hoicmvsao, jupiterhn9x và Hoang Dinh Nhat thích
Nguyễn Văn Tự Cường - Trường THPT Chuyên LQĐ - Quảng Trị
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh