Đề tuyển sinh vào lớp 10 THPT chuyên Nguyễn Trãi - Hải Dương 2017-2018
#1
 Đã gửi 03-06-2017 - 09:49
Đã gửi 03-06-2017 - 09:49

#2
 Đã gửi 03-06-2017 - 10:06
Đã gửi 03-06-2017 - 10:06

Chém câu bất trước:
Áp dụng bất đẳng thức $Cauchy – Schwarz$ ta có:$$2016 = \sqrt {{x^2} + {y^2}} + \sqrt {{y^2} + {z^2}} + \sqrt {{z^2} + {x^2}} \leqslant \sqrt {6\left( {{x^2} + {y^2} + {z^2}} \right)} \Rightarrow {x^2} + {y^2} + {z^2} \geqslant 6$$$$y + z \leqslant \sqrt {2\left( {{y^2} + {z^2}} \right)} ;\,\,x + z \leqslant \sqrt {2\left( {{x^2} + {z^2}} \right)} ;\,\,x + y \leqslant \sqrt {2\left( {{x^2} + {y^2}} \right)} $$Khi đó ta được:$$P = \frac{{{x^2}}}{{y + z}} + \frac{{{y^2}}}{{z + x}} + \frac{{{z^2}}}{{x + y}} \geqslant \frac{{{x^2}}}{{\sqrt {2\left( {{y^2} + {z^2}} \right)} }} + \frac{{{y^2}}}{{\sqrt {2\left( {{x^2} + {z^2}} \right)} }} + \frac{{{z^2}}}{{\sqrt {2\left( {{x^2} + {y^2}} \right)} }}$$$$ \geqslant \frac{{6 - \left( {{y^2} + {z^2}} \right)}}{{\sqrt {2\left( {{y^2} + {z^2}} \right)} }} + \frac{{6 - \left( {{x^2} + {z^2}} \right)}}{{\sqrt {2\left( {{x^2} + {z^2}} \right)} }} + \frac{{6 - \left( {{x^2} + {y^2}} \right)}}{{\sqrt {2\left( {{x^2} + {y^2}} \right)} }}$$$$ = \sum\limits_{cyc} {\frac{6}{{\sqrt {2\left( {{y^2} + {z^2}} \right)} }}} - \frac{1}{{\sqrt 2 }}\left( {\sqrt {{y^2} + {z^2}} + \sqrt {{x^2} + {z^2}} + \sqrt {{x^2} + {y^2}} } \right)$$$$\mathop \geqslant \limits^{AM - GM} \frac{{6.9}}{{\sum\limits_{cyc} {\sqrt {2\left( {{y^2} + {z^2}} \right)} } }} - \frac{1}{{\sqrt 2 }}\left( {\sqrt {{y^2} + {z^2}} + \sqrt {{x^2} + {z^2}} + \sqrt {{x^2} + {y^2}} } \right) = \frac{{3\sqrt 2 }}{2}$$
- bigway1906, NHoang1608, Tea Coffee và 2 người khác yêu thích
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#3
 Đã gửi 03-06-2017 - 10:12
Đã gửi 03-06-2017 - 10:12

- NHoang1608 yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#4
 Đã gửi 03-06-2017 - 10:17
Đã gửi 03-06-2017 - 10:17

Chém câu hệ. Ta có: $$PT\left( 2 \right) \Leftrightarrow \left( {x + y - 3} \right)\sqrt y + \left( {y - 1} \right)\left( {\sqrt {x + y + 1} - 2} \right) - x - y + 3 = 0$$$$ \Leftrightarrow \left( {x + y - 3} \right)\sqrt y + \frac{{\left( {y - 1} \right)\left( {x + y - 3} \right)}}{{\sqrt {x + y + 1} + 2}} - \left( {x + y - 3} \right) = 0$$$$ \Leftrightarrow \left( {x + y - 3} \right)\left( {\sqrt y + \frac{{y - 1}}{{\sqrt {x + y + 1} }} - 1} \right) = 0$$$$ \Leftrightarrow \left( {x + y - 3} \right)\left( {y - 1} \right)\left( {\frac{1}{{\sqrt {y + 1} }} + \frac{1}{{\sqrt {x + y + 1} }}} \right) = 0$$$$ \Leftrightarrow x + y = 3 \vee \,y = 1$$Đến đây thế vào $(1)$ là ra
- duylax2412 yêu thích
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#5
 Đã gửi 03-06-2017 - 10:18
Đã gửi 03-06-2017 - 10:18

3.1 Ta có: $x^{2}+5y^{2}-4xy +4x-4y+3=0 <=> (x-2y+2)^{2} +(y+2)^{2}=5=2^{2}+1^{2}$
Rồi tiếp tục
- tuaneee111 và duylax2412 thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#6
 Đã gửi 03-06-2017 - 10:43
Đã gửi 03-06-2017 - 10:43

Xin làm câu phương trình:
Câu 2:
1)
ĐKXĐ:$x \geq \frac{-3}{2}$
$pt \Leftrightarrow x(\sqrt{2x+3}-3)-\sqrt{x+5}(\sqrt{2x+3}-3)-(\sqrt{2x+3}-3)=0$
$\Leftrightarrow (\sqrt{2x+3}-3)(x-\sqrt{x+5}-1)=0$
Giả phương trình trên tìm được $2$ nghiệm là $x=3$ hay $x=4$ (chú ý phương trình thứ hai có điều kiện $x \geq 1$)
- Tea Coffee và Le Do Khoi 02 thích
Chỉ có hai điều là vô hạn: vũ trụ và sự ngu xuẩn của con người, và tôi không chắc lắm về điều đầu tiên.
Only two things are infinite, the universe and human stupidity, and I'm not sure about the former.
#7
 Đã gửi 03-06-2017 - 12:28
Đã gửi 03-06-2017 - 12:28

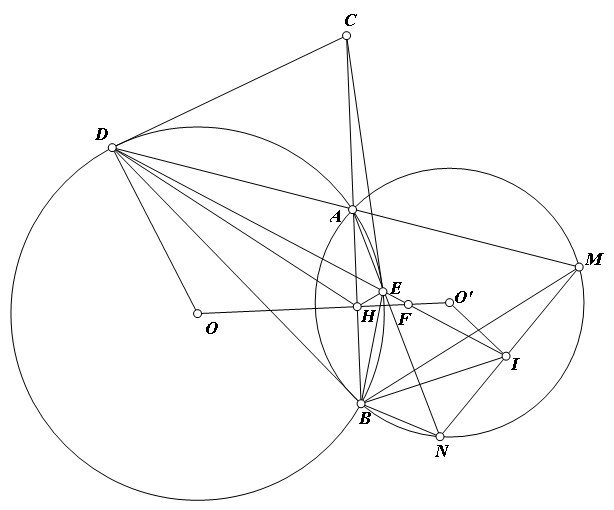
Làm câu hình ý a, c. Đại thì dễ mà hình cũng khó
a) Chứng minh được $CDOH, CDOE$ là các tứ giác nội tiếp $\Rightarrow O,D,C,E,H$ nằm trên cùng một đường tròn
$\Rightarrow \widehat{DHC}=\widehat{DEC}=\widehat{CDE}=\widehat{CHE}$ $\Rightarrow CH,HF$ là phân giác trong và ngoài $\widehat{DHE}$
Do đó: $\dfrac{HE}{HD}=\dfrac{FE}{FD}\iff FD.HE=FE.HD$
b) Hiện chưa làm được
c) Ta có: $\Delta CEB\sim \Delta CAE\Rightarrow \dfrac{CE}{CB}=\dfrac{AE}{BE}\\ \ \Delta CDA\sim \Delta CBD\Rightarrow \dfrac{CD}{CB}=\dfrac{AD}{BD}$
Mà: $CD=CE\iff \dfrac{AE}{BE}=\dfrac{AD}{BD}$
Lại có: $\widehat{BNI}=\widehat{BAD}=\widehat{BED}\iff BEIN$ nội tiếp
Do đó: $\widehat{BIN}=\widehat{BEN}=\widehat{BDA}\Rightarrow \Delta BNI \sim \Delta BAD\\ \Rightarrow \dfrac{BI}{IN}=\dfrac{BD}{AD}$
Tương tự: $\widehat{BIN}=\widehat{BEN}\Rightarrow \widehat{BIM}=\widehat{AEB};\hspace{0,5 cm}\widehat{BMI}=\widehat{BAE}\\ \Delta BIM \sim \Delta BEA\Rightarrow \dfrac{BI}{IM}=\dfrac{BE}{EA}$
Từ hai điều trên:
$\iff \dfrac{IN}{IM}=\dfrac{BD.AE}{AD.BE}=1\Rightarrow IN=IM\iff O'I\perp MN$
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 03-06-2017 - 12:32
- Nguyenphuctang, hagiang362002 và Le Do Khoi 02 thích
#8
 Đã gửi 03-06-2017 - 15:58
Đã gửi 03-06-2017 - 15:58

hình khó quá trời
" Khi ta đã quyết định con đường cho mình, kẻ được nói ta ngu ngốc chỉ có bản thân ta mà thôi. " _ Rononoa Zoro.
#9
 Đã gửi 04-06-2017 - 09:49
Đã gửi 04-06-2017 - 09:49

bài 1 ai làm được chưa
#10
 Đã gửi 04-06-2017 - 09:54
Đã gửi 04-06-2017 - 09:54

Câu 4.2 "Cho mình xin tạm cái hình"
Trong $(O)$ có $\widehat{BDE}=\widehat{BAE}$
Trong $(O')$ có $\widehat{BAE}=\widehat{BMI}$
$=> \widehat{BDE}=\widehat{BMI}=>$ Tứ giác $DMIB$ nội tiếp
$=> \widehat{ADI}=\widehat{BMI}$, mà $\widehat{ADI}=\widehat{ABE}$ nên $\widehat{ABE}=\widehat{MBI}$ kết hợp với $\widehat{BAN}=\widehat{BMN}$
Ta được $\bigtriangleup MIB\sim \bigtriangleup AEB(g-g)$
$=>\frac{MB}{IB}=\frac{BA}{EB}$ $=>\frac{MB}{IB}.\frac{EB.DI}{AN.BD}$
$=>\frac{BD}{ID}=\frac{AB}{NA}$ $=>AB.DI=AN.BD$
$=>\frac{AB.DI}{AN.BD}=1$ $(2)$
Từ $(1)$ và $(2)$ suy ra $\frac{MB.EB.DI}{IB.AN.BD}=1$
$=>MB.EB.DI=IB.AN.BD$
$=>$ ĐPCM
Bài viết đã được chỉnh sửa nội dung bởi Le Do Khoi 02: 04-06-2017 - 10:00
- hagiang362002, HoangKhanh2002 và NHoang1608 thích
#11
 Đã gửi 04-06-2017 - 10:38
Đã gửi 04-06-2017 - 10:38

Câu 1:
a.Ta có: $x+y+z=0$
$=>(x+y+z)(x^2+y^2+z^2-xy-yz-zx)+3xyz=3xyz$
$=>x^3+y^3+z^3=3xyz$
$=>$ $P= \frac{2018(x-y)(y-z)(z-x)}{2xy^2+2yz^2+2zx^2+3xyz}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2+x^3+y^3+z^3+xy^2+yz^2+zx^2}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2+y^2(x+y)+x^2(z+x)+z^2(z+y)}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}$ $($ do $x+y=-z, z+x=-y, y+z=-x$ $)$
$=2018$
Vậy: $P=2018$
#12
 Đã gửi 04-06-2017 - 10:50
Đã gửi 04-06-2017 - 10:50

Câu 1:
a.Ta có: $x+y+z=0$
$=>(x+y+z)(x^2+y^2+z^2-xy-yz-zx)+3xyz=3xyz$
$=>x^3+y^3+z^3=3xyz$
$=>$ $P= \frac{2018(x-y)(y-z)(z-x)}{2xy^2+2yz^2+2zx^2+3xyz}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2+x^3+y^3+z^3+xy^2+yz^2+zx^2}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2+y^2(x+y)+x^2(z+x)+z^2(z+y)}$
$=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}$ $($ do $x+y=-z, z+x=-y, y+z=-x$ $)$
$=2018$
Vậy: $P=2018$
Bài viết đã được chỉnh sửa nội dung bởi Le Do Khoi 02: 04-06-2017 - 11:09
#13
 Đã gửi 04-06-2017 - 11:10
Đã gửi 04-06-2017 - 11:10

Câu 1.b.
Ta có:
$1+ax=\frac{\sqrt{b}+\sqrt{2a-b}}{\sqrt{b}}$, $1-ax=\frac{\sqrt{b}-\sqrt{2a-b}}{\sqrt{b}}$
$=>\frac{1+ax}{1-ax}=\frac{\sqrt{b}+\sqrt{2a-b}}{\sqrt{b}-\sqrt{2a-b}}$
Làm tương tự ta được:
$\sqrt{\frac{1-bx}{1+bx}}=\sqrt{\frac{a-\sqrt{b(2a-b)}}{a-\sqrt{b(2a-b)}}}$
$=> Q=\frac{\sqrt{b}+\sqrt{2a-b}}{\sqrt{b}-\sqrt{2a-b}}.\sqrt{\frac{a-\sqrt{b(2a-b)}}{a-\sqrt{b(2a-b)}}}$
Do $0<a<b<2a$ nên $\frac{\sqrt{b}+\sqrt{2a-b}}{\sqrt{b}-\sqrt{2a-b}}>0$
$=> Q=\sqrt{(\frac{\sqrt{b}+\sqrt{2a-b}}{\sqrt{b}-\sqrt{2a-b}})^2.\frac{a-\sqrt{b(2a-b)}}{a-\sqrt{b(2a-b)}}}$
Thu gọn ta được: $Q=1$
Vậy: $Q=1$
#14
 Đã gửi 15-06-2017 - 07:29
Đã gửi 15-06-2017 - 07:29

Câu 3.2:
Không mất tính tổng quát, giả sử:$x\geq y$, khi đó: $x^{2}<x^{2}+3y<x^{2}+4x+4=(x+2)^{2} \Leftrightarrow x^{2}+3y=(x+1)^{2}$
(do $x^{2}+3y$ là số chính phương) $\Rightarrow 3y=2x+1$
rồi thay vào cái trên là xong
#15
 Đã gửi 25-06-2017 - 09:24
Đã gửi 25-06-2017 - 09:24

SỞ GIÁO DỤC VÀ ĐẠO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT
HẢI DƯƠNG CHUYÊN NGUYỄN TRÃI NĂM HỌC 2017 - 2018
Môn thi: TOÁN (Chuyên)
Thời gian làm bài: 150 phút, không kể thời gian giao đề
(Đề thi gồm có 01 trang)
Câu 1: (2,0 điểm)
1) Cho 3 số $x,y,z$ đôi một khác nhau và thỏa mãn điều kiện: $x+y+z=0$. Tính giá trị của biểu thức: $P=$ $\frac{2018(x-y)(y-z)(z-x)}{2xy^{2}+2yz^{2}+2zx^{2}+3xyz}$.
2) Rút gọn biểu thức : $Q=\frac{1+ax}{1-ax}$$\sqrt{\frac{1-bx}{1+bx}}$ với $x=\frac{1}{a}\sqrt{\frac{2a-b}{b}}$ và 0<a<b<2a.
Câu 2: (2,0 điểm)
1) Giải phương trình: $x\sqrt{2x+3}$ +$3(\sqrt{x+5}+1)$=$3x+$ $\sqrt{2x^{2}+13x+15}$+$\sqrt{2x+3}$
2) Giải hệ phươn trình: $\left\{\begin{matrix}x^{2}+4y-13 +(x-3)\sqrt{x^{2}+y-4}=0 \\ (x+y-3)\sqrt{y}+(y-1)\sqrt{x+y+1}=x+3y-5 \end{matrix}\right.$
Câu 3: (2,0 điểm)
1) Tìm nghiệm nguyên của phương trình:$x^{2}+5y^{2}-4xy+4x-4y+3=0$
2) Tìm tất cả các số nguyên dương $(x,y)$ thỏa mãn: $x^{2}+3y$ và $y^{2}+3x$ là số chính phương.
Câu 4: (3,0 điểm)
Cho hai đường tròn $(O;R),(O';R')$ cắt nhau tại hai điểm phân biệt $A,B$ (A,O,B không thẳng hàng). Trên tia đối của tia $AB$ lấy điểm $C$, kẻ tiếp tuyến CD, CE với (O), trong đó D,E là các tiếp điểm và E nằm trong (O'). Đường thẳng AD,AE cawsrt (O') lần lượt tại M,N (M,N khác A). Đường thẳng DE cắt MN tại I,OO' cắt AB và DI lần lượt tại H và F.
1) Chứng minh: FE.HD=FD.HE
2) Chứng minh: MB.EB.DI=IB.AN.BD
3) Chứng minh: O'I vuông góc với MN
Câu 5: (1,0 điểm)
Cho $x,y,z$ là bộ ba số dương thỏa mãn: $\sqrt{x^{2}+y^{2}}+\sqrt{y^{2}+z^{2}}+\sqrt{z^{2}+x^{2}}=6$. Tìm giá trị nhỏ nhất của biếu thức $M=\frac{x^{2}}{y+z}+\frac{y^{2}}{x+z}+\frac{z^{2}}{x+y}$
- NGUYENNAMYENTRUNG, Mr Cooper, NHoang1608 và 2 người khác yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
Được gắn nhãn với một hoặc nhiều trong số những từ khóa sau: 2017-2018, hải dương, tuyển sinh

|
Toán Trung học Cơ sở →
Tài liệu - Đề thi →
[TOPIC] Tổng hợp đề thi vào lớp 10 THPT các tỉnh, thành phố năm 2018-2019Bắt đầu bởi conankun, 09-06-2018 |
|
![[TOPIC] Tổng hợp đề thi vào lớp 10 THPT các tỉnh, thành phố năm 2018-2019 - bài viết cuối bởi DANG DUC QUY](https://diendantoanhoc.org/public/style_images/royal/profile/default_large.png)
|
|

|
Toán Trung học Cơ sở →
Hình học →
M thuộc đường thẳng cố định khi $d$ di động đi qua $M$.Bắt đầu bởi ViTuyet2001, 30-05-2018 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
CMR: $(a^2+1)(b^2+1) \ge (a+b)(ab+1)+5$Bắt đầu bởi dat102, 15-05-2018 |
|

|
|

|
Toán Trung học Cơ sở →
Bất đẳng thức và cực trị →
Tìm GTNN của $\frac{y}{x} + \frac{4x}{3y} + 15xy$Bắt đầu bởi dat102, 14-05-2018 |
|

|
|

|
Toán Trung học Cơ sở →
Hình học →
$PE+QF \geq PQ$Bắt đầu bởi ViTuyet2001, 29-04-2018 |
|

|
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh