Đề thi vào 10 chuyên Lam Sơn Thanh Hóa 2017-2018

Đề thi vào 10 chuyên Lam Sơn Thanh Hóa 2017-2018
#1
 Đã gửi 03-06-2017 - 14:28
Đã gửi 03-06-2017 - 14:28

- Saitohsuzuko001, NHoang1608, Tea Coffee và 1 người khác yêu thích
Chính trị chỉ cho hiện tại, nhưng phương trình là mãi mãi.
Politics is for the present, but an equation is for eternity.
#2
 Đã gửi 03-06-2017 - 15:20
Đã gửi 03-06-2017 - 15:20

Mình xin giải bài PT:
Đặt: $\sqrt[3]{x^3+5x^2}=a,\sqrt{\frac{5x^2-2}{6}}=b\geq 0$.
Ta có: $a-1=b$.
Từ cách đặt ta có:
$\left\{\begin{matrix}a^3-x^3=5x^2 \\ 6b^2+2=5x^2 \end{matrix}\right.\Rightarrow a^3-6b^2-2=x^3\Rightarrow (a-2)^3=x^3\Rightarrow a-2=x$
Từ đó, $x$ là nghiệm của PT: $(x+2)^3-x^3=5x^2\Leftrightarrow x^2+12x+8=0\Leftrightarrow x=2(-3\pm \sqrt{7})$.
Thử lại: $x=-6+2\sqrt{7}$ thỏa mãn.
Bài viết đã được chỉnh sửa nội dung bởi Baoriven: 03-06-2017 - 15:28
- etucgnaohtn, hoicmvsao, Tuan Duong và 8 người khác yêu thích
$$\mathbf{\text{Every saint has a past, and every sinner has a future}}.$$
#3
 Đã gửi 03-06-2017 - 15:45
Đã gửi 03-06-2017 - 15:45

Câu 3: a) Quy đồng ta được $A=\frac{a^{5}+10a^{4}+35a^{3}+50a^{2}+24a}{120}=\frac{a(a+1)(a+2)(a+3)(a+4)}{120}$
Vì $a,a+1,a+2,a+3,a+4$ là 5 số tự nhiên liên tiếp nên chia hết cho 3,5
Vì $a,a+1,a+2,a+3$ là 4 số tự nhiên liên tiếp nên có một số chia hết cho 4 và một số chia hết cho 2
=> $a(a+1)(a+2)(a+3)(a+4)\vdots 120 do (3,5,8)=1$ => ĐPCM.
- bigway1906, NHoang1608 và Lao Hac thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#4
 Đã gửi 03-06-2017 - 15:53
Đã gửi 03-06-2017 - 15:53

1. b. Ta có: $\left\{\begin{matrix}x=ny+pz \\ y=mx+pz \\ z=mx+ny \end{matrix}\right.$
$=> x+y+z=2(ny+pz+mx)=2(ny+y)=2y(n+1)=> \frac{1}{n+1}=\frac{2y}{x+y+z}$
Lại có,$x+y+z=2(pz+z)=2z(p+1)=>\frac{1}{p+1}=\frac{2z}{x+y+z}$
Và $x+y+z=2(mx+x)=2x(m+1)=>\frac{1}{m+1}=\frac{2x}{x+y+z}$
=> ĐPCM
- NHoang1608, 8A6 Cau Giay, Lao Hac và 2 người khác yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#5
 Đã gửi 03-06-2017 - 16:34
Đã gửi 03-06-2017 - 16:34

Câu 2.b.
Điều kiện: $x\neq 0$, $y>0$
Đặt: $\sqrt{y}= a (a>0)$
Khi đó hpt trở thành:$ \left\{\begin{matrix} \frac{x}{a}+\frac{2a}{x}=\frac{2}{x}+\frac{1}{a}-3& (1)\\ x^3-a^2x-9x+12=0 & (2) \end{matrix}\right.$
Biến đổi phương trình (1) trở thành:
$x^2+2a^2+3ax-2a-x=0$
$<=>x(a+x)+2a(a+x)-(2a+x)=0$
$<=>(2a+x)(a+x-1)=0$
TH1:
$2a+x=0 =>x=-2a$ thay vào phương trình $(2)$ ta được:
$(2)<=>-6a^3+18a+12=0$
$<=>(a-2)(a+1)(a+6)=0$
$=>a=2$ do a>0
$=>x=-4,y=4$ (Thử lại ta thấy thỏa mãn bài ra)
TH2:
$a+x-1=0 =>a=1-x$ thay vào phương trình $(2)$ ta được:
$(2)<=>x^2-5x+6=0$
$<=>x=2$ hoặc $x=3$
Với$x=2=>a=-1$(loại)
Với$x=3=>a=-2$(loại)
KL: Vậy Hệ phương trình đã cho có một nghiệm duy nhất $(x,y)=(-4,4)$
- Kiet Dep Trai yêu thích
#6
 Đã gửi 03-06-2017 - 17:14
Đã gửi 03-06-2017 - 17:14

#7
 Đã gửi 03-06-2017 - 17:16
Đã gửi 03-06-2017 - 17:16

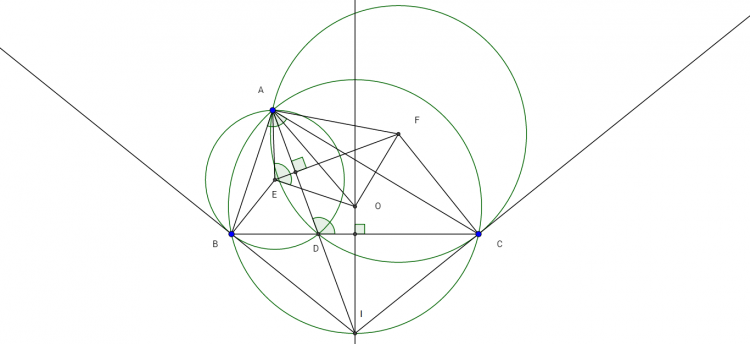
Câu 4
a.Ta có: $\widehat{CBI}=\widehat{BAI}$ (2 góc nội tiếp $(O)$ chắn 2 cung bằng nhau)
$=> BI$ là tiếp tuyến của $(E)=> \widehat{EBI}=90^o$
Lại có:
$\widehat{BAE}=\widehat{ABE}$(dễ dàng chứng minh)
$\widehat{AEO}=\widehat{AHE}+\widehat{HAE}=90^o+\widehat{HAE}=90^o+\widehat{HBE}=\widehat{ABI}=>\widehat{AEO}=\widehat{ABI}$ (1)
Mặt khác $\widehat{ABI}=\frac{1}{2}$sđ cung $ACI$ $=\frac{1}{2}(sđ cung AC+sđ cung CI)=\frac{1}{2}(sđ cung AC+sđ cung BI)=\widehat{ADC}$
$=>\widehat{ABI}=\widehat{ADC}$ (2)
Từ (1) và (2) suy ra: $\widehat{AEO}=\widehat{ADC}$ (*)
Chứng minh tương tự ta được: $\widehat{AFO}=\widehat{ADB}$ (**)
Từ (*) và (**) suy ra: $\widehat{AEO}+\widehat{AFO}=\widehat{ADB}+\widehat{ADC}=180^o$
$=> $ Tứ giác AEOF nội tiếp được
$=>$ ĐPCM
Bài viết đã được chỉnh sửa nội dung bởi Le Do Khoi 02: 03-06-2017 - 17:36
- hoicmvsao yêu thích
#8
 Đã gửi 03-06-2017 - 18:02
Đã gửi 03-06-2017 - 18:02

Lời giải Câu 4 của thầy Nguyễn Lê Phước

#9
 Đã gửi 03-06-2017 - 18:37
Đã gửi 03-06-2017 - 18:37

Bài 3
b. Ta có: $20412\vdots 2$ và $8y^2\vdots 2$ nên $x\vdots 2$
Đặt $x=2x_1$ Khi đó phương trình trở thành:
$5x_1^2+2y^2=5103$. Vì $5103\vdots 3$
Nên $5x_1^2+2x^2$ $\vdots 3$
Hay $x_1^2+ y^2 \vdots 3=>x_1,y\vdots 3$
Đặt $x_1=3x_2$ và $y=3y_1$ thì phương trình trở thành $5x_2^2+2y_1^2=567$
Suy luận tương tự ta cũng đặt $x_2=3x_3$ và $y_1=3y_2$, ta được $5x_3^2+2y_2^2=63$
Đặt $x_3=3x_4$ và $y_2=3y_3$,ta được $5x_4^2+2y_3^2=7$
Nếu $x_4=0,y_3=0$ thì phương trình đã cho vô nghiệm
Nếu $x_4y_3\neq 0$ thì $x_4=\pm 1$ và $y_3=\pm 1=>x=\pm 54, y=\pm 27$
Vậy $x=\pm 54, y=\pm 27$
Bài viết đã được chỉnh sửa nội dung bởi Le Do Khoi 02: 04-06-2017 - 08:21
- NHoang1608 yêu thích
#10
 Đã gửi 03-06-2017 - 20:44
Đã gửi 03-06-2017 - 20:44

Bài 3
b. Ta có: $20412\vdots 2$ và $8y^2\vdots 2$ nên $x\vdots 2$
Đặt $x=2x_1$ Khi đó phương trình trở thành:
$5x_1^2+2y^2=5103$. Vì $5103\vdots 3$
Nên $5x_1^2+2x^2$ $\vdots 3$
Hay $x_1^2+ y^2 \vdots 3=>x_1,y\vdots 3$
Đặt $x_1=3x_2$ và$y=3y_1$ thì phương trình trở thành $5x_2^2+2y_1^2=567$
Suy luận tương tự ta cũng đặt $x_2=3x_3$ và $y_1=3y_2$, ta được $5x_3^2+2y_2^2=63$
Đặt $x_3=3x_4$ và $y_2=3y_3$,ta được $5x_4^2+2y_3^2=7$
Nếu $x_4=0,y_3=0$ thì phương trình đã cho vô nghiệm
Nếu $x_4y_3\neq 0$ thì $x_4=\pm 1$ và $y_3=\pm 1=>x=\pm 54, y=\pm 24$
Vậy $x=\pm 54, y=\pm 24$
$y=27$ và $y=-27$ chớ
P/s: bài hôm nay làm tốt ko.Thấy thằng Kiệt làm được 9 đ thì phải
![]()
![]()
![]()
![]()
![]()
![]()
![]() I Love $\sqrt{MF}$
I Love $\sqrt{MF}$ ![]()
![]()
![]()
![]()
![]()
![]()
![]()
#11
 Đã gửi 03-06-2017 - 22:14
Đã gửi 03-06-2017 - 22:14

Đề thi vào 10 chuyên Lam Sơn Thanh Hóa 2017-2018
Câu 1a :
Bằng phương pháp quy nạp ta chứng minh được điều sau luôn đúng :
$P(n)=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{n(n+1)(n+2)}=\frac{n^2+3n}{4(n^2+3n+2)}$
Khi đó :
$S=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{2016.2017.2018}=P(2016)=\frac{4070304}{16281224}$
Vậy $S=\frac{4070304}{16281224}$
Tác giả :
Lương Đức Nghĩa
#12
 Đã gửi 03-06-2017 - 22:18
Đã gửi 03-06-2017 - 22:18

Câu 1a :
Bằng phương pháp quy nạp ta chứng minh được điều sau luôn đúng :
$P(n)=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{n(n+1)(n+2)}=\frac{n^2+3n}{4(n^2+3n+2)}$Khi đó :
$S=\frac{1}{1.2.3}+\frac{1}{2.3.4}+...+\frac{1}{2016.2017.2018}=P(2016)=\frac{4070304}{16281224}$Vậy $S=\frac{4070304}{16281224}$
mk nghĩ bài này dùng quy nạp khá phức tạp chỉ cần biến đổi mẫu là ok ![]()
![]()
![]()
- Lao Hac yêu thích
#13
 Đã gửi 04-06-2017 - 08:19
Đã gửi 04-06-2017 - 08:19

$y=27$ và $y=-27$ chớ
P/s: bài hôm nay làm tốt ko.Thấy thằng Kiệt làm được 9 đ thì phải
Mình không thi bạn à. Thế bạn có làm đc k?
Bài viết đã được chỉnh sửa nội dung bởi Le Do Khoi 02: 04-06-2017 - 08:19
#14
 Đã gửi 04-06-2017 - 09:51
Đã gửi 04-06-2017 - 09:51

Mình không thi bạn à. Thế bạn có làm đc k?
tạch mất câu chống liệt
- Le Do Khoi 02 yêu thích
![]()
![]()
![]()
![]()
![]()
![]()
![]() I Love $\sqrt{MF}$
I Love $\sqrt{MF}$ ![]()
![]()
![]()
![]()
![]()
![]()
![]()
#15
 Đã gửi 04-06-2017 - 09:56
Đã gửi 04-06-2017 - 09:56

tạch mất câu chống liệt
Đc khoảng bao nhiêu điểm thế bạn?
#16
 Đã gửi 04-06-2017 - 10:46
Đã gửi 04-06-2017 - 10:46

Đc khoảng bao nhiêu điểm thế bạn?
tạch mất câu chống liệt thì còn thi thố gì nữa
- Le Do Khoi 02 yêu thích
![]()
![]()
![]()
![]()
![]()
![]()
![]() I Love $\sqrt{MF}$
I Love $\sqrt{MF}$ ![]()
![]()
![]()
![]()
![]()
![]()
![]()
#17
 Đã gửi 04-06-2017 - 16:17
Đã gửi 04-06-2017 - 16:17

#18
 Đã gửi 04-06-2017 - 16:46
Đã gửi 04-06-2017 - 16:46

ai giải giùm tớ bài cuối được không?
giả sử có n đường
đường a cắt 2018 đường là b1;b2;....;b2018
suy ra a phải song song với n-2019 đường còn lại
vậy đường bi (với i chạy từ 1 đến 2018) cắt n-2019 đường này mà số đường bi có thể cắt thêm <= 2017 đường ( trừ đường a)
vậy n-2019<=2017 suy ra n<=4036 dấu = xảy ra <=> bi song song với 2017 đường có dạng bj ( j khác i và j chạy từ 1 đên 2018)
và a phải song song với 2017 đường còn lại không tính đường a và 2018 đường b1;b2;....;b2018
tức là có 2018 đường song song với nhau và vuông góc với 2018 đường còn lại
vậy max(n)=4036
Bài viết đã được chỉnh sửa nội dung bởi khgisongsong: 04-06-2017 - 16:47
- Kagome, AnhTran2911 và Le Do Khoi 02 thích
$\frac{(x!)^2.(-1)^x+1}{2x+1}\in Z $ (với $x\in N)<=>2x+1$ là số nguyên tố
#19
 Đã gửi 04-06-2017 - 17:46
Đã gửi 04-06-2017 - 17:46

#20
 Đã gửi 04-06-2017 - 17:56
Đã gửi 04-06-2017 - 17:56

@khgisongsong: hình như ko cần vuông góc vẫn t/m mà bạn, chỉ cần 2018 đường song song và 2018 đường kia cx song song và ko song song với 2018 đường ở trên
uk đúng rồi cảm ơn bạn
$\frac{(x!)^2.(-1)^x+1}{2x+1}\in Z $ (với $x\in N)<=>2x+1$ là số nguyên tố
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh