Đề thi vào 10 chuyên TPHCM 2017-2018

Đề thi vào 10 chuyên TPHCM 2017-2018
#1
 Đã gửi 03-06-2017 - 17:15
Đã gửi 03-06-2017 - 17:15

- NGUYENNAMYENTRUNG, HoangKhanh2002, Kiratran và 5 người khác yêu thích
Chính trị chỉ cho hiện tại, nhưng phương trình là mãi mãi.
Politics is for the present, but an equation is for eternity.
#2
 Đã gửi 03-06-2017 - 18:05
Đã gửi 03-06-2017 - 18:05

Mình xin chém bất trước. Ta có: \[\frac{{16\sqrt {xy} }}{{x + y}} + \frac{{{x^2} + {y^2}}}{{xy}} = \frac{{{{\left( {\sqrt x - \sqrt y } \right)}^4}\left( {4\sqrt {xy} + x + y} \right)}}{{xy\left( {x + y} \right)}} + 10 \geqslant 10\]
- NHoang1608, Tea Coffee và hoangtuyeuai2809 thích
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#3
 Đã gửi 03-06-2017 - 18:19
Đã gửi 03-06-2017 - 18:19

Xin chém câu 2
a) Từ phương trình suy ra: $4(x+2)^2(3x-1)=(3x^2-7x-3)^2\iff 9x^4-54x^3-13x^2+10x+25=0\\\iff (x^2-7x+5)(9x^2+9x+5)=0\\ \iff x=\dfrac{7\pm \sqrt{29}}{2}$
Thử lại thấy $x=\dfrac{7+ \sqrt{29}}{2}$
b) ĐK: $x,y\neq 0$. Hệ đã cho tương đương với: $\left\{\begin{matrix} x^2y+x-10y+xy=0\\ 20y^2-xy-y=1 \end{matrix}\right.\iff \left\{\begin{matrix} x^2y+x-10y+xy=0\\ 20xy^2-x^2y-xy=x \end{matrix}\right.\\\Rightarrow 20xy^2-10y=0\iff 10y(2xy-1)=0$
Đến đây tự giải
- NHoang1608, hoangtuyeuai2809 và conankun thích
#4
 Đã gửi 03-06-2017 - 18:36
Đã gửi 03-06-2017 - 18:36

Câu 1b)
Ta có $(m+n)^{2}< (m+n)^{2}+3m+n+1 < (m+n+2)^{2}$
Suy ra $A=(m+n+1)^{2}$
$\Rightarrow (m+n)^{2}+3m+n+1= (m+n+1)^{2}$
$\Leftrightarrow m=n+1$
$\Leftrightarrow n=m-1$
Từ đó suy ra $n^{k}+1 = (m-1)^{k}+ 1 \vdots m$ với mọi $k$ lẻ. Tổng quát lên k lẻ luôn vì chẳng thấy bậc mấy cả ![]() .
.
- IHateMath, Kagome, Kiratran và 6 người khác yêu thích
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
----- Michelangelo----
#5
 Đã gửi 03-06-2017 - 19:04
Đã gửi 03-06-2017 - 19:04

Chính trị chỉ cho hiện tại, nhưng phương trình là mãi mãi.
Politics is for the present, but an equation is for eternity.
#6
 Đã gửi 03-06-2017 - 21:56
Đã gửi 03-06-2017 - 21:56

1. a) Ta có: $a+b+c =3; a^{2}+b^{2}+c^{2}=29; abc =11$
=> $(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2bc+2ac=9=> 2(ab+ac+bc)=9-29=-20=> ab+ac+bc=-10$
Lại có,$(a+b+c)(ab+bc+ac)=a^{2}b+ab^{2}+a^{2}c+ac^{2}+b^{2}c+bc^{2}+3abc=(-10).3=-30 => a^{2}b+ab^{2}+a^{2}c+ac^{2}+b^{2}c+bc^{2}+2abc=-30-11=-41=>(a+b)(b+c)(a+c)=-41$
Mặt khác, $a^{3}+b^{3}+c^{3}=(a+b+c)^{3}-3(a+b)(a+c)(b+c)=27-3(-41)=150$
- NHoang1608 yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#7
 Đã gửi 03-06-2017 - 22:01
Đã gửi 03-06-2017 - 22:01

Ai ghi đề 1.b hộ e được không,mờ quá e không nhìn được
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#8
 Đã gửi 04-06-2017 - 11:59
Đã gửi 04-06-2017 - 11:59

Đề bài $1$ đúng ra phải là tính $a^5+b^5+c^5$. Tuy nhiên câu này rất có vấn đề. Theo định lý Viete, $a,b,c$ là nghiệm của phương trình $$x^3-3x^2-10x-11=0.$$
tuy nhiên phương trình này chỉ có một nghiệm thực duy nhất. Vậy tại sao trong đề lại nói là "$a,b,c$ là các số thực..."???
- duylax2412 và truongphat266 thích
#9
 Đã gửi 04-06-2017 - 13:20
Đã gửi 04-06-2017 - 13:20

Bài $6$. Đây là một biến thể của bài toán Ramsey nổi tiếng: "Trong $9$ người bất kỳ, luôn tìm được $3$ người quen nhau hoặc $4$ người đôi một không quen nhau.
Trở lại bài toán của ta. Gọi các điểm là $P_i$ ($i=1,2,\dots 9$). Với mỗi $i$ ta lại đặt $R(i)$ là số cạnh đỏ kẻ từ $P_i$ và $B(i)$ là số cạnh xanh kẻ từ $P_i$. Rõ ràng, $R(i)+B(i)=8$. Giả sử phản chứng rằng trong một bộ $4$ điểm bất kỳ thì có ít nhất một cạnh xanh. Ta sẽ cmr với mọi $i$, $B(i)=3$ và $R(i)=5$. Thật vậy, giả sử tồn tại một đỉnh $P_j$ sao cho $B(j)=4$. Khi đó xét bộ bốn điểm nối với $P_j$ bởi các cạnh xanh. Vì có ít nhất một cạnh xanh nối $2$ trong $4$ điểm này nên kết quả là sẽ tồn tại một tam giác xanh, vô lí. Mặt khác, nếu $B(j)=2$, hay $R(j)=6$, thì theo kết quả của bài toán sau (chính là bài toán Ramsey): "Trong $6$ điểm bất kỳ thì tồn tại ít nhất một tam giác có các cạnh cùng màu", trong $6$ điểm nối với $P_j$ bởi các cạnh đỏ, do không thể có một tam giác xanh, nên sẽ có một tam giác đỏ; khi đó tam giác này và $P_j$ tạo thành một bộ $4$ không có cạnh nào xanh, trái với giả thiết phản chứng. Như vậy, tóm lại là $R(i)=5$ với mọi $i$. Vậy $$\sum{R(i)}=5\cdot 9=45.$$
Mặt khác, dễ thấy $\sum{R(i)}$ lại bằng hai lần số cạnh đỏ, nên đẳng thức trên không thể xảy ra, tức là giả thiết phản chứng của chúng ta sai. Bài toán được giải quyết.
- bigway1906, NHoang1608, Tea Coffee và 1 người khác yêu thích
#10
 Đã gửi 04-06-2017 - 13:35
Đã gửi 04-06-2017 - 13:35

Bài $4$. Bài toán này khá hay, vận dụng tư tưởng giảm biến như sau: Chia cả tử và mẫu của hai phân thức lần lượt cho $y, y^2$ ta thu được $$16\cdot\frac{\sqrt{x/y}}{x/y+1}+\frac{(x/y)^2+1}{x/y}=16\cdot\frac{\sqrt{x/y}}{x/y+1}+\frac{(x/y+1)^2}{x/y}-2.$$
Đặt ẩn mới $t=\frac{\sqrt{x/y}}{x/y+1}$ (chú ý rằng $0<t\leq 2$ theo bđt Cauchy) thì bài toán trở thành: Tìm GTNN của $$P=16t+\frac{1}{t^2}-2\quad (0<t\leq 2).$$
Để giải quyết bài toán mới này, ta chỉ cần áp dụng bđt Cauchy cho $3$ số (cái này đi thi phải chứng minh lại) như sau $$P=8t+8t+1/t^2-2\geq 3\sqrt[3]{8t\cdot 8t\cdot \frac{1}{t^2}}-2=12-2=10.$$ Dấu "=" xảy ra khi và chỉ khi $8t=\frac{1}{t^2}$, tức là $t=2$ hay $x=y$.
- Tea Coffee và sunsin thích
#11
 Đã gửi 04-06-2017 - 13:41
Đã gửi 04-06-2017 - 13:41

Các em cấp THCS làm gì được học khái niệm hàng điểm điều hòa mà xài Maclaurin nhỉ?
#12
 Đã gửi 04-06-2017 - 15:32
Đã gửi 04-06-2017 - 15:32

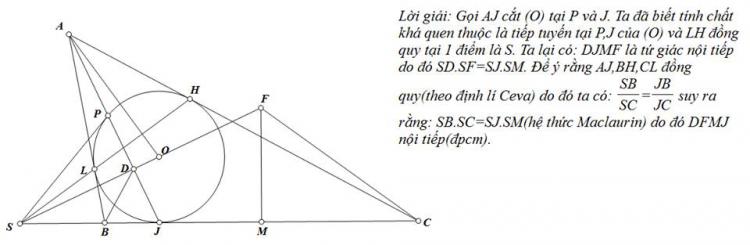
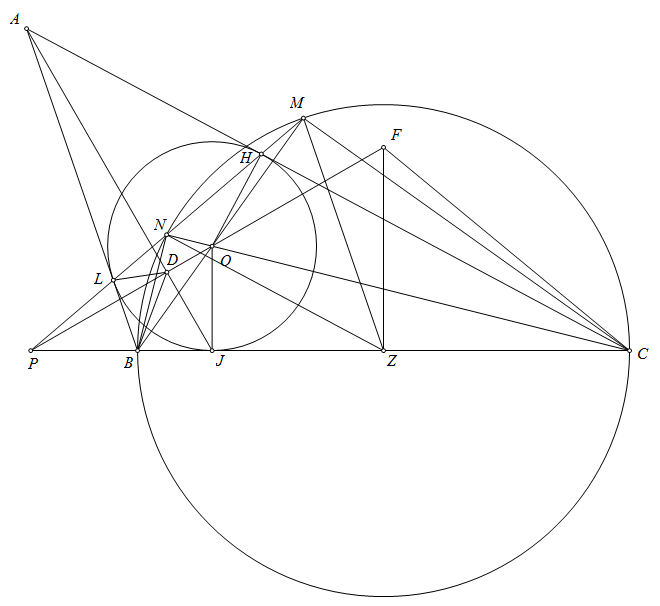
Cách khác câu hình :
$FD \cap CB = P$. Ta dễ dàng chứng minh : $P,L,H,M$ thẳng hàng (Chứng minh bằng hệ thức lượng đường tròn)
Gọi $Z$ là trung điểm $BC$.
Ta có:
$$\angle NJB = \angle NOB = \angle MHC $$
Mà $$ \angle NMZ = \dfrac{180^{\circ} - \angle NZM }{ 2} = \dfrac{180^{\circ} - 2 \angle OCM }{2 } = 90^{\circ} -\angle OCM = \angle MOC $$
$$ \Rightarrow \angle NJB = \angle NMZ \Rightarrow \text{ Tứ giác NMZJ nội tiếp } $$
Áp dụng hệ thức lượng đường tròn cho các tứ giác nội tiếp: $BNMC, NMZJ$ :
$$ PM.PN = PJ.PZ =PB.PC $$
Từ đó suy ra : $DFCB $ là tứ giác nội tiếp.
Cách này tuy hoàn toàn $ \text{THCS}$ vì $\text{Hệ thức lượng đường tròn có thể chứng minh bằng kiến thức THCS}$
#13
 Đã gửi 04-06-2017 - 15:50
Đã gửi 04-06-2017 - 15:50

Câu 4
Ta có : P = $\frac{8\sqrt{ab}}{a+b}+\frac{8\sqrt{ab}}{a+b}+\frac{(a+b)^{2}}{ab}-2$$\geq 12-2=10$
bài này dễ
- Tea Coffee yêu thích
#14
 Đã gửi 26-06-2017 - 20:35
Đã gửi 26-06-2017 - 20:35

Mình xin chém bất trước. Ta có: \[\frac{{16\sqrt {xy} }}{{x + y}} + \frac{{{x^2} + {y^2}}}{{xy}} = \frac{{{{\left( {\sqrt x - \sqrt y } \right)}^4}\left( {4\sqrt {xy} + x + y} \right)}}{{xy\left( {x + y} \right)}} + 10 \geqslant 10\]
#15
 Đã gửi 04-07-2017 - 13:52
Đã gửi 04-07-2017 - 13:52

Câu 3a chỉ cần gọi phân giác thì do cân nên nó thành đường cao 3 đc cắt nhau tai tâm nội tiếp ABC
#16
 Đã gửi 31-05-2018 - 13:53
Đã gửi 31-05-2018 - 13:53

3b kiểu gì
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh