Đề thi tuyển sinh môn toán chuyên tỉnh Ninh Bình năm 2017-2018
#1
 Đã gửi 03-06-2017 - 18:21
Đã gửi 03-06-2017 - 18:21

- Saitohsuzuko001, NTMFlashNo1, Mr Cooper và 2 người khác yêu thích
The greatest danger for most of us is not that our aim is too high and we miss it, but that it is too low and we reach it.
----- Michelangelo----
#2
 Đã gửi 03-06-2017 - 18:29
Đã gửi 03-06-2017 - 18:29

Đề quá dễ (Đại)
Câu 2:
a) Đặt: $\left\{\begin{matrix} \sqrt{x+4}=a\geqslant 0\\ \sqrt{x-1}=b\geqslant 0 \end{matrix}\right.\Rightarrow (a-b)(ab+1)=a^2-b^2\iff (a-b)(a-1)(b-1)=0$
b) Hệ đã cho: $\left\{\begin{matrix} x^3-3x=y^3+y\\ x^2=y^2+3 \end{matrix}\right.\iff \left\{\begin{matrix} x^3-y^3=3x+y\\ x^2-y^2=3 \end{matrix}\right.\\\Rightarrow 3(x^3-y^3)=(x^2-y^2)(3x+y)\iff (x-y)(2y^2-xy)=0$
Câu 3:
a) $\sqrt{(a^2+2018)(b^2+2018)(c^2+2018)}=\sqrt{(a^2+ab+bc+ca)(b^2+ab+bc+ca)(c^2+ab+bc+ca)}=(a+b)(b+c)(c+a)$
b) Từ $7x^2+3y^2=714$ $\Rightarrow \left\{\begin{matrix} 3y^2 \vdots 7\\ 3y^2\leqslant 714 \end{matrix}\right.\Rightarrow y^2\in \left \{ 49,196 \right \}$...
Câu cuối cứ ra đi ra lại mà không chán
Câu 5
Thay $2018$ vào mẫu mỗi phân thức
$\sum \dfrac{a}{a+\sqrt{2018a+bc}}=\sum \dfrac{a}{a+\sqrt{a(a+b+c)+bc}}=\sum \dfrac{a}{a+\sqrt{ab+(a^2+bc)+ac}}\\ \leqslant^{AM-GM} \sum \dfrac{a}{a+\sqrt{(\sqrt{ab}+\sqrt{ac})^2}}=\sum \dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1$
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 03-06-2017 - 18:40
- HoangTienDung1999, NHoang1608 và Tea Coffee thích
#3
 Đã gửi 03-06-2017 - 18:37
Đã gửi 03-06-2017 - 18:37

Xin chém câu bất trước ![]()
Ta có: $\frac{a}{a+\sqrt{2018a+bc}}$= $\frac{a}{a+\sqrt{a^{2}+ab+ac+bc}}$=$\frac{a}{a+\sqrt{(a+b)(b+c)}}$
$\leq\frac{a}{a+\sqrt{ab}+\sqrt{ac}}$ (BĐT Bunhiacopxki)
$\doteq \frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}$
CMTT $\Rightarrow$ P$\leq$1
Đẳng thức xảy ra $\Leftrightarrow$ a=b=c=$\frac{2018}{3}$
Vậy Max P=1 $\Leftrightarrow a=b=c=\frac{2018}{3}$
P/s: ai gõ telex hộ đi mình nhìn số mũ hơi mờ
Bài viết đã được chỉnh sửa nội dung bởi linhk2: 03-06-2017 - 18:39
- Tea Coffee yêu thích
#4
 Đã gửi 03-06-2017 - 18:42
Đã gửi 03-06-2017 - 18:42

Câu 2a: ĐK: x>=1
đặt căn(x+4)=a; căn(x-1)=b (a,b>=0) => a^2-b^2 = 5
pt <=> (a-b)(ab+1) = a^2-b^2
<=> (a-b)(a-1)(b-1)=0
Xét các trường hợp rồi đối chiếu vs ĐK để tìm nghiệm
Câu 3a thay 2017 = ab+bc+ca vào biểu thức chứa căn
=> căn((a^2+2017)(a^2+2017)(a^2+2017)) = (a+b)(b+c)(c+a) là số hữu tỉ vì a, b, c hữu tỉ.
#5
 Đã gửi 03-06-2017 - 18:43
Đã gửi 03-06-2017 - 18:43

Câu 3a:
Ta có: $\sqrt{(a^{2}+2017)(b^{2}+2017)(c^{2}+2017)}= (a+b)(b+c)(c+a)$
Mà a,b,c hữu tỉ nên suy ra đpcm
#6
 Đã gửi 03-06-2017 - 18:49
Đã gửi 03-06-2017 - 18:49

Câu 3b
ta thấy $7x^{2}\vdots7$
$714\vdots 7$
$\Rightarrow 3y^{2}\vdots 7$
$\Rightarrow y^{2}\vdots 7$
$\Rightarrow y\vdots 7$
Mà $3y^{2}\leq 714\Rightarrow y\in \left \{ 0;7;14 \right \}$
tự thay vào tìm x
Bài viết đã được chỉnh sửa nội dung bởi linhk2: 03-06-2017 - 18:50
- NHoang1608 yêu thích
#7
 Đã gửi 03-06-2017 - 20:02
Đã gửi 03-06-2017 - 20:02

Chấp nhận giới hạn của bản thân, nhưng đừng bao giờ bỏ cuộc
#8
 Đã gửi 03-06-2017 - 21:55
Đã gửi 03-06-2017 - 21:55

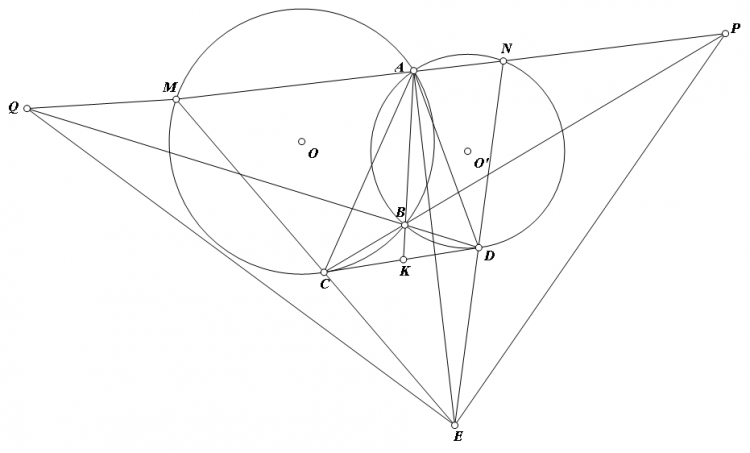
Làm luôn bài hình, quá dễ
a) Ta có: $\widehat{ECD}=\widehat{AMC}=\widehat{ACE}$. Tương tự: $\widehat{CDE}=\widehat{CDA}$
Từ đó: $CD$ là trung trực của $AE$
b) Dễ thấy: $\left\{\begin{matrix} \widehat{BCD}=\widehat{BAC}\\ \widehat{BDC}=\widehat{BAD} \end{matrix}\right.\Rightarrow \widehat{CBD}=180^o-\widehat{BCD}-\widehat{BDC}\\\iff \widehat{CBD}=180^o-\widehat{CAD}=180^o-\widehat{CED}\Rightarrow BCED$ nội tiếp
c) Gọi $K$ là giao điểm của $AB$ và $CD$
Nhận thấy: $\left\{\begin{matrix} \Delta BCK \sim \Delta CAK \Rightarrow KC^2=KB.KA\\ \Delta DBK \sim \Delta ADK \Rightarrow KD^2=KB.KA \end{matrix}\right.\Rightarrow KC=KD$
$CD//PQ\Rightarrow \dfrac{KD}{AQ}=\dfrac{KC}{AP}\Rightarrow AQ=QP; \\AE\perp PQ\Rightarrow \Delta EPQ$ cân tại E
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 03-06-2017 - 21:58
- HoangTienDung1999 và Nguyen Xuan Hieu thích
#9
 Đã gửi 05-06-2017 - 19:05
Đã gửi 05-06-2017 - 19:05

Bài hình bỏ $a,b$ là đề đề nghị của Russia. Cũng là đề của Hưng Yên năm ngoái.
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh