Đề thi vào 10 chuyên tỉnh Bắc Giang 2017-2018

Đề thi vào 10 chuyên tỉnh Bắc Giang 2017-2018
#1
 Đã gửi 07-06-2017 - 23:40
Đã gửi 07-06-2017 - 23:40

- Tea Coffee và khoaitokhonglochetdoi thích
Chính trị chỉ cho hiện tại, nhưng phương trình là mãi mãi.
Politics is for the present, but an equation is for eternity.
#2
 Đã gửi 08-06-2017 - 07:31
Đã gửi 08-06-2017 - 07:31

II.1)Vì 2 vế của phương trình đều dương nên bình phương hai vế, ta được:$2x^{2}-x+4-3x+2\sqrt{(2x^{2}-x)(4-3x)}=4(x^{2}-2x+2) <=> 2x^{2}-4x+4+2\sqrt{8x^{2}-6x^{3}-4x+3x^{2}}=4x^{2}-8x+8 <=>8x^{2}-6x^{3}-4x+3x^{2}=(x^{2}-2x+2)^{2}=x^{4}+4x^{2}+4-4x^{3}-8x+4x^{2}<=>x^{4}+2x^{3}-3x^{2}-4x+4=0 <=>(x-1)^{2}(x+2)=0$
Bài viết đã được chỉnh sửa nội dung bởi Tea Coffee: 08-06-2017 - 07:47
- khoaitokhonglochetdoi yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#3
 Đã gửi 08-06-2017 - 08:02
Đã gửi 08-06-2017 - 08:02

I.1.b) Bình phương 2 vế pt ta được:$\frac{x^{2}}{16}=\frac{1009+\sqrt{2017}}{2}+\frac{1009-\sqrt{2017}}{2}-2\sqrt{\frac{1009^{2}-2017}{4}}=1009-2.504=1=>x^{2}=16...$
- khoaitokhonglochetdoi yêu thích
Treasure every moment that you have!
And remember that Time waits for no one.
Yesterday is history. Tomorrow is a mystery.
Today is a gift. That’s why it’s called the present.
#4
 Đã gửi 08-06-2017 - 09:59
Đã gửi 08-06-2017 - 09:59

Chém câu bất
Ta có: $P=\dfrac{y}{x}+\dfrac{x}{y}+\dfrac{1}{3}\dfrac{x}{y}+3xy+12xy+\dfrac{4}{3}-\dfrac{4}{3}\\\geqslant 2+2x+8\sqrt{xy}-\dfrac{4}{3}\\=2x+\dfrac{2}{3}+8\sqrt{xy}\geqslant 4\sqrt{\dfrac{x}{3}}+8\sqrt{xy}=4$
Dấu "=" xảy ra: $\iff x=y=\dfrac{1}{3} \square$
câu hệ làm kiểu gì nhỉ?
Anh gõ lại đề giùm em, em chả thấy gì?
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 09-06-2017 - 08:52
- HoangTienDung1999 yêu thích
#5
 Đã gửi 08-06-2017 - 13:52
Đã gửi 08-06-2017 - 13:52

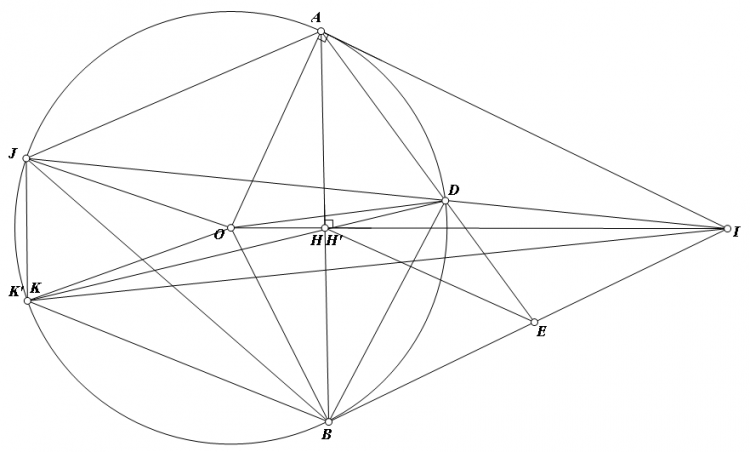
Câu hình
a) $HE$ là đường trung bình $\Delta BAI\Rightarrow \widehat{BHE}=\widehat{BAI}=\widehat{BAD}+\widehat{DAI}=\widehat{BAD}+\widehat{DBA}=\widehat{BDE}$
Do đó: $BHDE$ nội tiếp
b) Kẻ $IK'//AB, H'$ là giao điểm của $DK'$ và $AB$
Khi đó: $\Delta ADH' \sim \Delta JDB \implies \dfrac{AH'}{DH'}=\dfrac{JB}{DB}\\ \Delta BDH' \sim \Delta JDA \implies \dfrac{BH'}{DH'}=\dfrac{JA}{DA}$
Mà: $\left\{\begin{matrix} \Delta IDA \sim \Delta IAJ\\ \Delta IDB \sim \Delta IBJ \end{matrix}\right. \implies \dfrac{JB}{DB}=\dfrac{JA}{DA} \implies BH'=AH'\implies$ $H$ trùng $H'$, $K$ trùng $K'$
Do đó: $IK//AB$. Dễ dàng suy ra được: $\Delta BJA$ cân tại B
c) Dễ thấy $ID.IJ=IA^2=IH.IO \implies$ $JOHD$ nội tiếp. Kết hợp $JKBA$ là hình thang cân $\implies \Delta IJK$ cân tại $I$
Do đó: $\dfrac{ID}{HI}=\dfrac{IO}{IJ}=\dfrac{IO}{IK} \implies ID.IK=IO.IH$
Mà: $HO.HI=HA.HB=HD.HK$
Trừ theo vế: $ID.IK-HD.HK=(IO-HO)IH=IH^2$
Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 08-06-2017 - 13:54
- HoangTienDung1999 và Tea Coffee thích
#6
 Đã gửi 08-06-2017 - 23:22
Đã gửi 08-06-2017 - 23:22

câu hệ làm kiểu gì nhỉ?
#7
 Đã gửi 09-06-2017 - 09:34
Đã gửi 09-06-2017 - 09:34

Đề thi vào 10 chuyên tỉnh Bắc Giang 2017-2018
$(\frac{x}{y}+\frac{y}{x})+(\frac{x}{3y}+12xy)+(3xy+\frac{4}{3})-\frac{4}{3}$ rồi dùng Cauchy cho các cặp số trong ngoặc là ok ![]()
- Tea Coffee và khoaitokhonglochetdoi thích
=> do what you love and love what you do <=
#8
 Đã gửi 13-06-2017 - 10:30
Đã gửi 13-06-2017 - 10:30

Câu 3 :
Đặt $\frac{x+y\sqrt{2017}}{y+z\sqrt{2017}}=k(k\in Q) \Leftrightarrow x+y\sqrt{2017}=k(y+z\sqrt{2017}) \Leftrightarrow x-ky=(zk-y)\sqrt{2017} \Leftrightarrow \left\{\begin{matrix} x-ky=0\\y-kz=0 \end{matrix}\right.\Leftrightarrow x=ky=k^{2}z$
Đặt $x=k^{2}z;y=kz$, ta có: $(kz+2)(4k^{2}z^{2}+6kz-3)=(y+2)(4y^{2}+6y-3)$
Dễ dàng chứng minh $y+2$ và $4y^{2}+6y-3$ là nguyên tố cùng nhau, do đó cả 2 số đều là số chính phương, tìm được y, đến đây chỉ là việc của bạn thôi
Bài viết đã được chỉnh sửa nội dung bởi khoaitokhonglochetdoi: 14-06-2017 - 08:14
#9
 Đã gửi 13-06-2017 - 14:36
Đã gửi 13-06-2017 - 14:36

.
Bài viết đã được chỉnh sửa nội dung bởi khoaitokhonglochetdoi: 13-06-2017 - 14:47
#10
 Đã gửi 13-06-2017 - 14:43
Đã gửi 13-06-2017 - 14:43

Câu 5(phiên bản dễ hiểu)
Đầu tiên, bạn chọn điểm rơi(tức là đoán nghiệm), tìm ra $x=y=\frac{1}{3}$
Ta có $P=\frac{y}{x}+\frac{4x}{3y}+15xy$
Bài viết đã được chỉnh sửa nội dung bởi khoaitokhonglochetdoi: 13-06-2017 - 14:46
#11
 Đã gửi 12-11-2017 - 15:40
Đã gửi 12-11-2017 - 15:40

đè bài dễ nhìn
File gửi kèm
#12
 Đã gửi 17-11-2017 - 22:55
Đã gửi 17-11-2017 - 22:55

đè bài dễ nhìn
Câu !b) đề bài phải là x13 và x23 các bạn nhé
Bài viết đã được chỉnh sửa nội dung bởi NGUYENNAMYENTRUNG: 17-11-2017 - 22:56
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh