Chủ đề này có 6 trả lời

[huykinhcan99]

Vòng 1.
Câu 1 (1,0 điểm). Không dùng máy tính cầm tay hãy giải phương trình $x^2+2x-8=0$.

 

Câu 2 (1,0 điểm). Cho hàm số bậc nhất $y=\left(2m-3\right) x +5m-1$ ($m$ là tham số, $m\neq \dfrac{3}{2}$).

1. Tìm $m$ để hàm số nghịch biến trên $\mathbb{R}$.
2. Tìm $m$ để đồ thị hàm số cắt trục tung tại điểm có tung độ là $-6$.

Câu 3 (1,0 điểm). Không dùng máy tính cầm tay, rút gọn biểu thức

\[A=\left(\sqrt{8}-3\sqrt{2} +2\sqrt{5} \right) \left(\sqrt{2}+10\sqrt{0,2}\right)\]

 

Câu 4 (1,0 điểm). Cho $B=\left(\dfrac{x}{\sqrt{x}+3}-\dfrac{x+1}{\sqrt{x}-3} +\dfrac{6x+\sqrt{x}}{x-9}\right):\left(\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-1\right)$ với $\left\{ \begin{array}{l} x\geqslant 0 \\ x\neq 9\end{array} \right.$. Hãy rút gọn biểu thức $B$ và tính giá trị của $B$ khi $x=12+6\sqrt{3}$.

 

Câu 5 (1,0 điểm). Cho hệ phương trình $\left\{ \begin{array}{l} mx-y=n \\ nx+my=1\end{array} \right.$ ($m$, $n$ là tham số).

1. Không dùng máy tính cầm tay hãy giải hệ phương trình khi $m=-\dfrac{1}{2}$, $n=\dfrac{1}{3}$.
2. Xác định các tham số $m$ và $n$ biết rằng hệ phương trình có nghiệm là $\left(-1, \sqrt{3}\right)$.

Câu 6 (1,0 điểm). Cho phương trình $2x^2+3x-1=0$. Gọi $x_1$, $x_2$ là hai nghiệm phân biệt của phương trình. Không giải phương trình, hãy tính giá trị của biểu thức:

\[P=2\left(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}\right)\]

 

Câu 7 (1,0 điểm).  Một tam giác vuông có cạnh huyền bằng $5\ \mathrm{cm}$, diện tích là $6\ \mathrm{cm}^2$. Tính độ dài các cạnh góc vuông của tam giác vuông đó.

 

Câu 8 (1,0 điểm). Hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A$ và $B$. Gọi $M$ là trung điểm của $OO'$. Qua $A$ kẻ đường thẳng vuông góc với $AM$ cắt các đường tròn $(O)$ và $(O')$ lần lượt ở $C$ và $D$. Chứng minh rằng $AC=AD$.

 

Câu 9 (1,0 điểm). Cho đường tròn $(O)$, đường kính $AB$, cung $\overarc{CD}$ nằm cùng phía đối với $AB$ ($D$ thuộc cung nhỏ $\overarc{BC}$). Gọi $E$ là giao điểm của $AC$ và $BD$, $F$ là giao điểm của $AD$ và $BC$.

1. Tính góc $\widehat{AFB}$ khi số đo của cung $\overarc{CD}$ bằng $80^\circ$.
2. TÍnh số đo cung $\overarc{CD}$ khi góc $\widehat{AEB}$ bằng $55^\circ$.

Câu 10 (1,0 điểm). Cho tam giác nhọn $ABC$ ($AB<AC$). Đường tròn tâm $O$ đường kính $BC$ cắt cạnh $AC$, $AB$ lần lượt tại $D$ và $E$. $H$ là giao điểm của $BD$ và $CE$, $K$ là giao điểm của $DE$ và $AH$, $F$ là giao điểm của $AH$ và $BC$. $M$ là trung điểm của $AH$. Chứng minh rằng $MD^2=MK.MF$.

 

Vòng 2.
Câu 1 (1,0 điểm). Không dùng máy tính cầm tay hãy rút gọn $A=\dfrac{\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{10}+\sqrt{2}}$.
 
Câu 2 (2,0 điểm). Giải hệ phương trình sau
\[\left\{ \begin{array}{l} x^2+y^2-xy+4y+1=0\\ y\left(7-x^2-y^2+2xy\right)=2\left(x^2+1\right) \end{array} \right.\]
 
Câu 3 (1,0 điểm). Cho số tự nhiên $A=\overline{\underbrace{777\ldots 7}_{n \text{ chữ số } 7}}-18+2n$ với $n\in \mathbb{N}, n\geqslant 2$. Chứng minh rằng $A$ chia hết cho $9$.
 
Câu 4 (1,5 điểm). Cho $a$, $b$, $c$ là các số dương thoả mãn $a+b+c\leqslant \sqrt{3}$. Tìm giá trị lớn nhất của biểu thức
\[P=\dfrac{a}{\sqrt{a^2+1}} + \dfrac{b}{\sqrt{b^2+1}} + \dfrac{c}{\sqrt{c^2+1}}\]
 
Câu 5 (1,0 điểm). Với mỗi số nguyên dương $n$ ta ký hiệu $a_n$ là số nguyên gần $\sqrt{n}$ nhất. Ví dụ $a_1=1$, $a_2=1$, $a_3=2$, $a_4=2$, $a_5=2$, $a_6=2$, $a_7=3$. Tính giá trị của tổng:
\[s=\dfrac{1}{a_1}+\dfrac{1}{a_2}+\ldots+\dfrac{1}{a_{2017}}+\dfrac{1}{a_{2018}}\]
 
Câu 6 (1,0 điểm). Cho hai đường tròn tâm $O_1$ và $O_2$ nằm ngoài nhau. ĐOạn thẳng $O_1O_2$ cắt đường tròn $(O_1)$ tại điểm $A$. Phần kéo dài của đoạn $O_1O_2$ cắt đường tròn $(O_2)$ tại $B$. Dựng đường tròn tâm $O$ tiếp xúc ngoài với đường tròn $(O_1)$ tại $D$ và tiếp xúc trong với đường tròn $(O_2)$ tại $C$ (điểm $O$ không nằm trên đoạn $O_1O_2$). Chứng minh rằng các điểm $A$, $B$, $C$, $D$ cùng nằm trên một đường tròn.
 
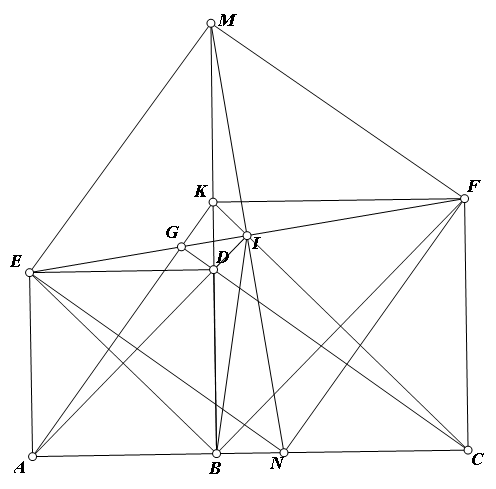
Câu 7 (2,5 điểm). Cho ba điểm $A$, $B$, $C$ phân biệt thẳng hàng và theo thứ tự đó sao cho $AB<BC$. Trong một nửa mặt phẳng có bờ là đường thẳng $AC$ dựng các hình vuông $ABDE$ và $BCFK$. Gọi $I$ là trung điểm của đoạn thẳng $EF$. Đường thẳng qua $I$ vuông góc với $EF$ cắt các đường thẳng $BD$ và $AB$ lần lượt tại $M$ và $N$. Chứng minh rằng:

• Tứ giác $AEIN$ và tứ giác $EMID$ nội tiếp được trong đường tròn.
• Ba điểm $A$, $I$, $D$ thẳng hàng và các điểm $B$, $N$, $F$, $M$, $E$ nằm trên cùng một đường tròn.
• Ba đường thẳng $AK$, $EF$, $CD$ đồng quy.

[HoangKhanh2002]

Câu 3 (1,0 điểm). Cho số tự nhiên $A=\overline{\underbrace{777\ldots 7}_{n \text{ chữ số } 7}}-18+2n$ với $n\in \mathbb{N}, n\geqslant 2$. Chứng minh rằng $A$ chia hết cho $9$.

 Câu 4 (1,5 điểm). Cho $a$, $b$, $c$ là các số dương thoả mãn $a+b+c\leqslant \sqrt{3}$. Tìm giá trị lớn nhất của biểu thức
\[P=\dfrac{a}{\sqrt{a^2+1}} + \dfrac{b}{\sqrt{b^2+1}} + \dfrac{c}{\sqrt{c^2+1}}\]

Câu 3:

Ta có: $A=\underbrace{77..77}_{n}-18+2n=7.\dfrac{10^n-1}{9}-18+2n=7.\dfrac{10^n-1-9n}{9}-18+9n$

Chỉ cần chứng minh: $10^n-9n-1 \vdots 81,n\geqslant 2$ bằng quy nạp

Câu 4:

$\sqrt{3}\geqslant a+b+c\geqslant \sqrt{3(ab+bc+ca)} \implies ab+bc+ca\leqslant 1$

Thay vào: $P=\sum \dfrac{a}{\sqrt{a^2+1}}\leqslant \sum \dfrac{a}{\sqrt{(a+b)(a+c)}}\leqslant \dfrac{1}{2} \sum \left (\dfrac{a}{a+b}+\dfrac{a}{a+c} \right )=\dfrac{3}{2}$

PS: huykinhcan99: Em gõ nhanh nên thiếu căn

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 08-06-2017 - 15:24

[huykinhcan99]

Câu 3:

Ta có: $A=\underbrace{77..77}_{n}-18+2n=7.\dfrac{10^n-1}{9}-18+2n=7.\dfrac{10^n-1-9n}{9}-18+9n$

Chỉ cần chứng minh: $10^n-9n-1 \vdots 81,n\geqslant 2$ bằng quy nạp

Câu 4:

$\sqrt{3}\geqslant a+b+c\geqslant \sqrt{3(ab+bc+ca)} \implies ab+bc+ca\leqslant 1$

Thay vào: $P=\sum \dfrac{a}{a^2+1}\leqslant \sum \dfrac{a}{(a+b)(a+c)}\leqslant \dfrac{3}{2}$

 

 

Hình như có vấn đề ở chỗ bôi đỏ
P.s: hình như câu 3 quy nạp trực tiếp được Thử với $n=2$, $A=63 \ \vdots \ 9$, đúng. Giả sử đúng đến $n$, tức là

\[\overline{\underbrace{777\ldots 7}_{n \text{ chữ số } 7}}-18+2n \ \vdots \ 9\]

 

Ta cần chứng minh bài toán đúng với $n+1$, tức là

\[\overline{\underbrace{777\ldots 7}_{n+1 \text{ chữ số } 7}}-18+2\left(n+1\right) \ \vdots \ 9\]

 

Thật vậy:

\[\overline{\underbrace{777\ldots 7}_{n+1 \text{ chữ số } 7}}-18+2\left(n+1\right)= 7.10^n+ \overline{\underbrace{777\ldots 7}_{n \text{ chữ số } 7}}-18+2n +2 = \left(\overline{\underbrace{777\ldots 7}_{n \text{ chữ số } 7}}-18+2n\right)+\left(7.10^n+2\right)\]

 

Chú ý rằng, với $n\geqslant 2$, ta có ngay $7.10^n+2=\underbrace{700\ldots 02}_{n-1 \text{ chữ số } 0}$, có tổng các chữ số là $9$, do đó $7.10^n+2 \ \vdots \ 9$.

 

Vậy bài toán đúng với $n+1$. Theo quy nạp có điều phải chứng minh

Bài viết đã được chỉnh sửa nội dung bởi huykinhcan99: 08-06-2017 - 15:25

[adteams]

$3=(x+y+z)^2 \geq 3(xy+yz+zx) => 1\geq \sum xy$ 

$P\leq  \sum \frac{x}{\sqrt{x^2+xy+yz+xz}} = \sum \frac{x}{\sqrt{(x+y)(x+z)}}\leq \frac{1}{2}\sum (\frac{x}{x+y}+\frac{x}{x+z}) = \frac{3}{2}$
P/s: Đề năm nay khó hơn năm ngoái nhiều câu hay hơn <3 - Bạn #HoangKhanh2002 nhanh tay quá :3
T^T Thông cảm mình nhầm (x;y;z)=(a;b;c) :v

Bài viết đã được chỉnh sửa nội dung bởi adteams: 08-06-2017 - 15:16

[adteams]

#Câu_Hệ
\[\left\{\begin{matrix}

x^2+1=-y(y-x+4) &  & \\ 

 y(7-x^2-y^2+2xy)=2(x^2+1)&  & 

\end{matrix}\right.\]

\[\left\{\begin{matrix}

x^2+1=-y(y-x+4) &  & \\ 

 y(7-x^2-y^2+2xy)=2-y(y-x+4)&  & (II)

\end{matrix}\right.\]

$(II) <=> y=0$

$<=>(7-x^2-y^2+2xy)=2-(y-x+4) <=> (x-y-3)(x-y+5)=0$....đến đây thì dễ rùi

Bài viết đã được chỉnh sửa nội dung bởi adteams: 08-06-2017 - 15:33

[bigway1906]

Câu bất mình dùng Bunhia, 

$P^2 \leq  (a+b+c)(\frac{a}{a^2+1}+\frac{b}{b^2+1}+\frac{c}{c^2+1})$

$\sum \frac{a}{a^2+1} \leq  \sum \frac{a}{4\sqrt[4]{\frac{a^2}{27}}} = \frac{1}{4\sqrt[4]{\frac{1}{27}}}\sum \sqrt{a}\leq \frac{1}{4\sqrt[4]{\frac{1}{27}}} .\sqrt{3\sqrt{3}}= \frac{3\sqrt{3}}{4}$

Vậy $P \leq  3/2$

Bài viết đã được chỉnh sửa nội dung bởi bigway1906: 08-06-2017 - 16:07

[HoangKhanh2002]

Câu 10 (1,0 điểm). Cho tam giác nhọn $ABC$ ($AB<AC$). Đường tròn tâm $O$ đường kính $BC$ cắt cạnh $AC$, $AB$ lần lượt tại $D$ và $E$. $H$ là giao điểm của $BD$ và $CE$, $K$ là giao điểm của $DE$ và $AH$, $F$ là giao điểm của $AH$ và $BC$. $M$ là trung điểm của $AH$. Chứng minh rằng $MD^2=MK.MF$.

Bài này khá dễ

Dễ dàng chứng minh được $H$ là tâm đường tròn nội tiếp $\Delta DEF$

Nhận thấy $M$ là tâm $(AEHD)$ $\implies \widehat{HMD} =2\widehat{HED}=\widehat{FED} \implies EMDF$ nội tiếp

$\implies \widehat{MDE}=\widehat{MFE}=\widehat{MFD}$

Do đó: $\Delta MDK \sim \Delta MFD \implies MD^2=MD.MK$

 

Câu 7 (2,5 điểm). Cho ba điểm $A$, $B$, $C$ phân biệt thẳng hàng và theo thứ tự đó sao cho $AB<BC$. Trong một nửa mặt phẳng có bờ là đường thẳng $AC$ dựng các hình vuông $ABDE$ và $BCFK$. Gọi $I$ là trung điểm của đoạn thẳng $EF$. Đường thẳng qua $I$ vuông góc với $EF$ cắt các đường thẳng $BD$ và $AB$ lần lượt tại $M$ và $N$. Chứng minh rằng:

• Tứ giác $AEIN$ và tứ giác $EMID$ nội tiếp được trong đường tròn.
• Ba điểm $A$, $I$, $D$ thẳng hàng và các điểm $B$, $N$, $F$, $M$, $E$ nằm trên cùng một đường tròn.
• Ba đường thẳng $AK$, $EF$, $CD$ đồng quy.

1. Khỏi làm

2. Dễ thấy $\Delta EBF$ vuông tại $E$ nên $IE=IB$

Do đó: $\overline{A,D,I}$

Tứ giác $EDIM$ nội tiếp $\implies \widehat{IEM}=\widehat{IDM}=45^o$ $\implies IE=IM=IB$

$\Delta BMN$ có $IB=IM \implies IN=IB=IM$

$EBFM$ có 2 đường chéo vuông góc với nhau tại TĐ, bằng nhau. Dễ dàng chứng minh $B,E,M,F,N$ cùng thuộc đường tròn

3. Dễ thấy: $BE//KC$, $AD\perp BE\implies AD\perp KC \implies D$ là trực tâm $\Delta AKC \implies CD \perp AK$ tại $G$

Lúc đó: $EGDA, GKFC$ nội tiếp $\implies \widehat{EGA}=\widehat{EDA}=45^o$; $\widehat{KGF}=\widehat{KCF}=45^o$ nên $\overline{E,G,F}$

PS: Sao dễ vậy nhỉ???

Bài viết đã được chỉnh sửa nội dung bởi HoangKhanh2002: 08-06-2017 - 16:17