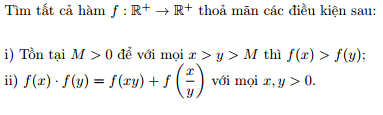Chủ đề này có 1 trả lời

[Drago]

[foollock holmes]

Thế $x=y=1$ vào ii ta có được $f(1)=2$. 

Thế $x=1$ ta có $f(x)=f(\frac{1}{x})$(1)

Thế $y=x$ ta có được $f(x)^2=f(x^2)+2$

Giả sử $M<1$ thì tồn tại $x$ sao cho $x>\frac{1}{x} >M$ 

mà ta có $f(x)=f(\frac{1}{x})$ nên không thỏa (i)

Vậy $M \geq 1$. Giả sử tồn tại $ x>y>1$ sao cho $f(x)\leq f(y)$ 

vì $x,y>1$ nên tồn tại $n \in \mathbb{N}$ sao cho $x^{2^{n}} >y^{2^{n}} >M$ 

suy ra $f(x^{2^n}) >f(y^{2^n})$ (2)

Từ (1) và (2) ta suy ra $f(x^{2^{n-1}})>f(y^{2^{n-1}}) $ 

Tương tự suy ra $f(x)>f(y)$. Vô lí 

Vậy ta có $f(x)$ đồng biến trên $[1, + \infty)$

.... từ đây thì nó giống với bài trong imo 2003 shortlist trong đây 

https://anhngq.files...3-shortlist.pdf

bài a5 ý bạn