Như vậy hai bài toán Tuần 4 tháng 6/2017 đã được đưa lời giải tại đây kèm theo đó là hai bài toán mới của thầy Trần Quang Hùng và anh Trịnh Huy Vũ. Xin trích dẫn lại hai bài toán:
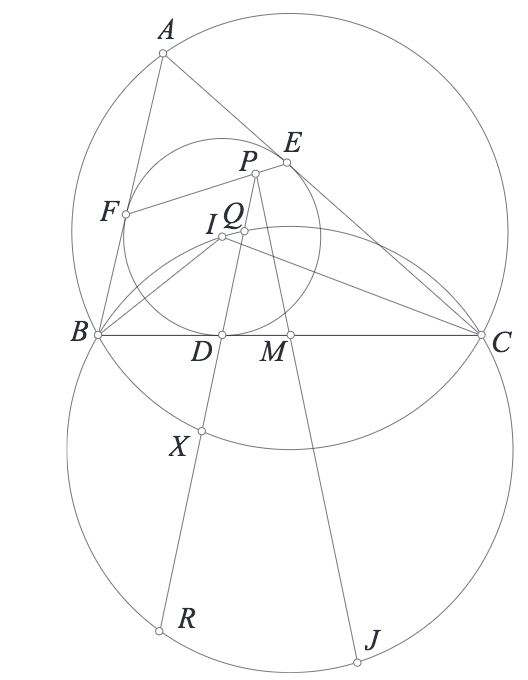
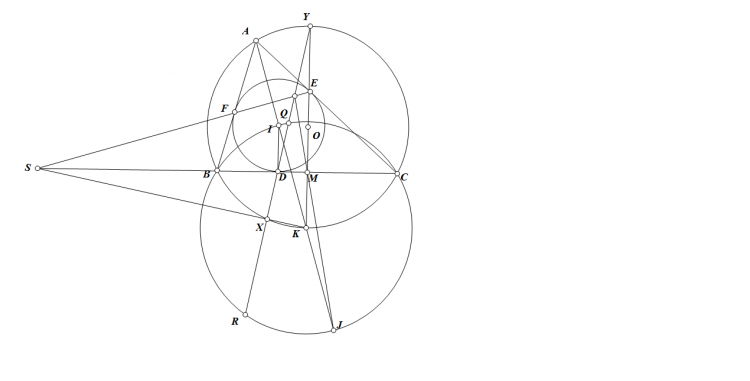
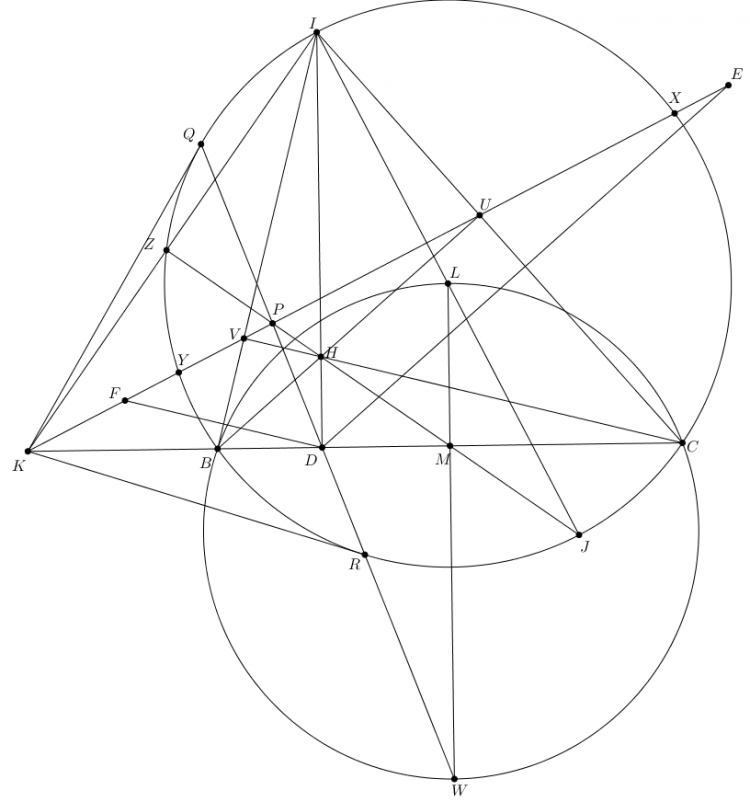
Bài 1. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. $J$ là tâm bàng tiếp gód $A$. $M$ là trung điểm của $BC$. $MJ$ cắt $EF$ tại $P$. $PD$ cắt đường tròn $(BIC)$ tại $Q,R$. Chứng minh rằng trung điểm của $QR$ nằm trên đường tròn ngoại tiếp tam giác $ABC$.
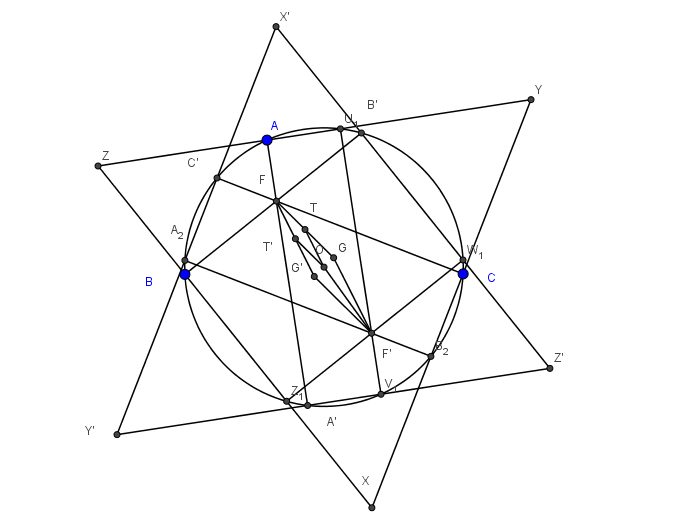
Bài 2. (Trịnh Huy Vũ) Cho tam giác $ABC$ nội tiếp $(O)$ có điểm Fermat là $F$. $FA,FB,FC$ cắt $(O)$ lần lượt tại $X,Y,Z$ khác $A,B,C$. Chứng minh rằng đường thẳng $OF$ chia đôi đoạn nối trực tâm của hai tam giác $ABC$ và $XYZ$.
Bài viết đã được chỉnh sửa nội dung bởi Zaraki: 02-07-2017 - 23:54