$$ \huge \text{USA TSTST 2017} $$
Ngày thứ nhất
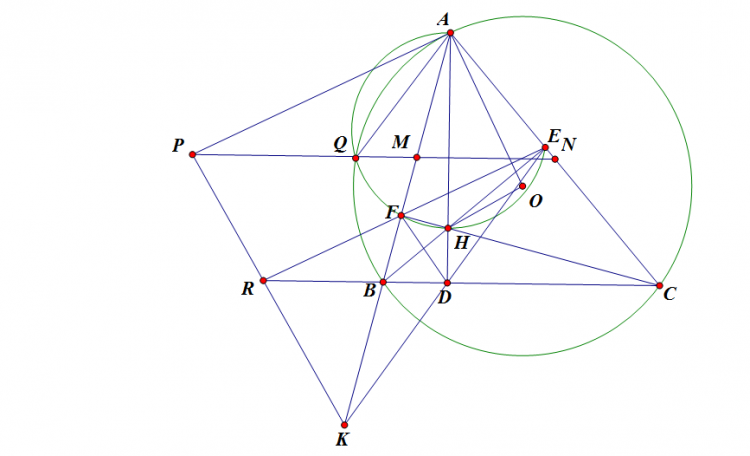
Bài 1. Cho tam giác $\displaystyle ABC$ nội tiếp đường tròn $\displaystyle \Gamma$ có tâm $\displaystyle O$, và trực tâm $\displaystyle H$. Giả sử $\displaystyle AB\neq AC$ và $\displaystyle \angle A \neq 90^{\circ}$. Gọi $\displaystyle M$ và $\displaystyle N$ lần lượt là trung điểm của $\displaystyle AB$ và $\displaystyle AC$, và $\displaystyle E$ và $\displaystyle F$ lần lượt là chân các đường cao hạ từ $\displaystyle B$ và $\displaystyle C$ của tam giác $\displaystyle ABC$. Gọi $\displaystyle P$ là giao điểm của $\displaystyle MN$ với tiếp tuyến của $\displaystyle \Gamma $ tại $\displaystyle A$. Gọi $\displaystyle Q$ là giao điểm thứ hai của $\displaystyle \Gamma$ với $\displaystyle (AEF)$. Gọi $\displaystyle R$ là giao điểm của $\displaystyle AQ$ và $\displaystyle EF$. Chứng minh rằng $\displaystyle PR \perp OH$.
Bài 2. Ana và Banana đang chơi một trò như sau: Đầu tiên Ana chọn một từ, là dãy khác rỗng các chữ cái trong bảng chữ cái tiếng Anh. Sau đó Banana chọn một số tự nhiên $\displaystyle k$ và đố Ana đưa ra một từ có đúng $\displaystyle k$ dãy con bằng với từ của Ana. Ana thắng nếu có thể đưa ra một từ như thế, nếu không, cô ấy sẽ thua. Từ nào mà khi Ana chọn cô ấy sẽ luôn thắng với mọi cách chọn $\displaystyle k$ của Banana?
Bài 3. Xét phương trình $\displaystyle x^2-cx+1 = \dfrac{f(x)}{g(x)}$, ở đây $\displaystyle f$ và $\displaystyle g$ là các đa thức với hệ số thực không âm. Với $\displaystyle c>0$, xác định giá trị nhỏ nhất của $\displaystyle \deg f$ hoặc chứng tỏ $\displaystyle f,g$ không tồn tại.
Ngày thứ hai
Bài 4. Tìm nghiệm tự nhiên của $$\displaystyle 2^a + 3^b + 5^c = n!$$
Bài 5. Cho tam giác $\displaystyle ABC$ với tâm nội tiếp $\displaystyle I$. Gọi $\displaystyle D$ là điểm trên cạnh $\displaystyle BC$ và $\displaystyle \omega_B, \displaystyle \omega_C$ lần lượt là đường tròn nội tiếp của các tam giác $\displaystyle ABD, \displaystyle ACD$. Giả sử $\displaystyle \omega_B$ và $\displaystyle \omega_C$ tiếp xúc với đoạn $\displaystyle BC$ lần lượt tại $\displaystyle E$ và $\displaystyle F$. Gọi $\displaystyle P$ là giao điểm của đoạn $\displaystyle AD$ với đường thẳng nối các tâm của $\displaystyle \omega_B$ và $\displaystyle \omega_C$. Gọi $\displaystyle X$ là giao điểm của $\displaystyle BI$ và $\displaystyle CP$, $\displaystyle Y$ là giao điểm của $\displaystyle CI$ và $\displaystyle BP$. Chứng minh $\displaystyle EX$ và $\displaystyle FY$ cắt nhau trên đường tròn nội tiếp của tam giác $\displaystyle ABC$.
Bài 6. Dãy $\displaystyle (a_n)_{n \ge 1}$ các số nguyên dương được gọi là một dãy kiểu Fibonacci nếu $\displaystyle a_{n + 2} = a_{n + 1} + a_n$ với mọi $\displaystyle n \ge 1$. Liệu có thể phân hoạch tập các số nguyên dương thành vô hạn dãy kiểu Fibonacci?
Nguồn: Thầy Nguyễn Trung Tuân