Âm thanh mà ta nghe được, dù đó là nhạc, lời nói hay những tiếng ồn trong đám đông đều là kết quả của sự dao động trong màng nhĩ lỗ tai, được mô phỏng bằng sóng âm lan truyền trong không khí phát ra từ tai nghe, âm thanh nhạc cụ, tiếng nói của con người hay từ một kẻ vô duyên nói luyên thuyên sau lưng bạn khi xem phim ngoài rạp. Khi vẽ đồ thị những dao động này theo cường độ hay áp suất theo thời gian, ta được biểu diễn hình ảnh của âm thanh.


Sóng âm thanh phát ra từ âm thoa (ảnh trên) và sóng âm thanh phát ra khi con người nói (ảnh dưới)
Đồ thị sóng âm phát ra từ cây âm thoa hình chữ $A$ là ví dụ cho sóng sine, ký hiệu toán học là $\sin \left( x \right)$, còn đồ thị sóng âm của tiếng nói thì có dạng phức tạp hơn. Tuy nhiên, bất kỳ sóng âm nào, hay có thể nói bất kỳ hàm tuần hoàn nào cũng đều có thể tách thành một số các sóng sine với những tần số và cường độ khác nhau. Kết quả này là công trình nghiên cứu của nhà Toán học người Pháp có tên Joseph Fourier, ông sinh vào thế kỷ 18 trong cuộc Cách mạng Pháp. Biểu thức của sóng âm hay bất kỳ tín hiệu thay đổi theo thời gian được biểu diễn theo các sóng sine được gọi là biểu diễn Fourier của tín hiệu đó.
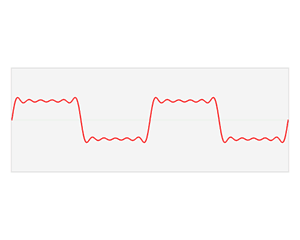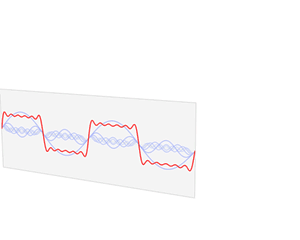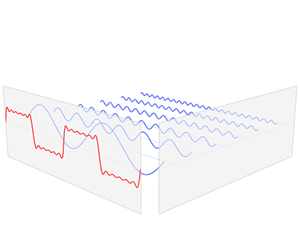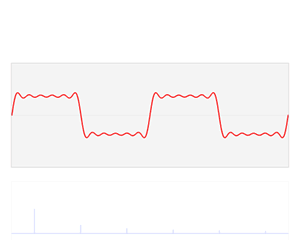
Hàm $f$ thay đổi theo thời gian biểu diễn sóng âm. Quy trình biến đổi Fourier dùng hàm $f$ và phân rã thành các sóng sine tương ứng với cường độ và tần số riêng biệt. Ta biểu diễn biến đổi Fourier thành các đỉnh gai trong miền tần số, chiều cao mỗi đỉnh gai biểu diễn biên độ sóng của tần số đó
Bạn có thể xem hình ảnh là một hàm biến đổi, tuy nhiên, hàm biến đổi này không biến đổi theo thời gian mà biến đổi theo không gian 2 chiều của ảnh. Đối với ảnh xám, mỗi điểm ảnh có giá trị từ 0 đến 255 biểu diễn cường độ ảnh. Do đó, cường độ của điểm ảnh là một hàm số theo toạ độ trục tung và trục hoành tương ứng với vị trí của điểm ảnh đó. Bạn có thể xem ảnh như một cảnh có những gợn sóng nhấp nhô, với chiều cao của cảnh tương ứng với giá trị của điểm ảnh.
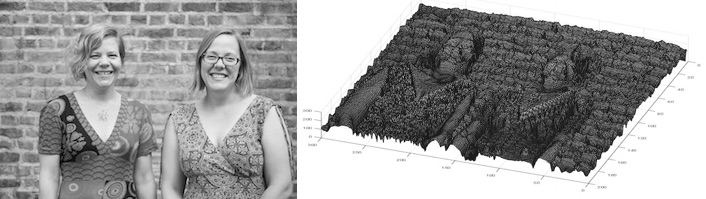
Một tấm ảnh số được đăng trên tạp chí Plus, mỗi điểm ảnh có giá trị từ 0 đến 255 biểu diễn mức xám của điểm ảnh. Ảnh bên phải là hàm ảnh của ảnh bên trái, với mỗi giá trị xám $u\left( x,y \right)$ là chiều cao của bề mặt trong mặt phẳng $\left( x,y \right)$
Ta có thể biểu diễn ảnh thành tổng các sóng sine, nhưng thay vì biểu diễn theo sóng một chiều thì ta biểu diễn theo hai chiều, giống như những gợn sóng trên sông.
Sóng sine 2 chiều được viết là
$$z=a\sin \left( hx+ky \right)$$
với $x$ và $y$ là toạ độ của điểm trên “sông”, $z$ là độ cao (hay cường độ) của sóng tại điểm đó, còn $a$ là biên độ (độ cao lớn nhất) của sóng, còn $h$ và $k$ là số lần sóng lặp lại theo chiều $x$ và $y$ riêng biệt (tức tần số $x$ và $y$).
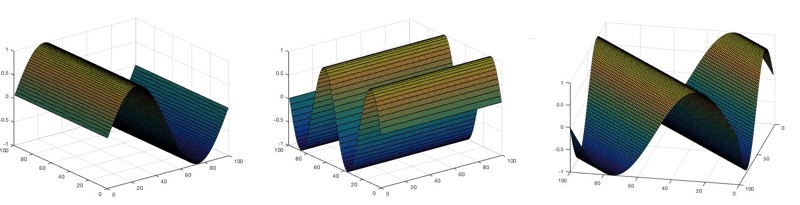
Đồ thị sóng $\sin \left( x \right),\sin \left( 2y \right)$ và $\sin \left( x+y \right)$
Khi $k=0$, sóng sine chỉ dao động dọc theo trục $x$. Khi $h=0$, sóng sine chỉ dao động theo trục $y$. Nhưng nếu $k$ và $h$ khác 0, sóng sine dao động theo chiều chéo theo mặt phẳng theo hướng góc nhất định (vuông góc với sóng trước) và độ dốc là $h/k$.
Cộng những sóng này lại tương đương với cộng những giá trị riêng biệt (hay độ cao) của sóng tại mỗi điểm ảnh. Các sóng này giao thoa cùng pha tạo thành sóng cuối cùng có giá trị cao hơn tại điểm đó hay giao thoa ngược pha và triệt tiêu nhau. Nếu biên độ của một trong các sóng cao hơn các sóng còn lại thì sóng đó sẽ có ưu thế hơn.
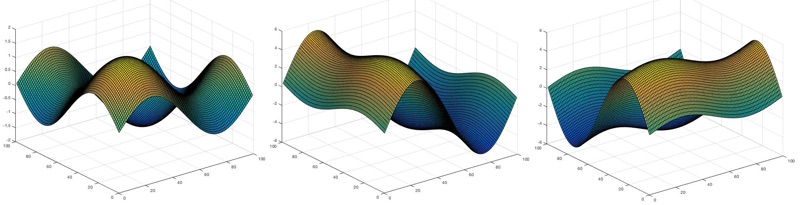
Các sóng $\sin \left( x \right)+\sin \left( y \right),5\sin \left( x \right)+\sin \left( y \right)$ và $\sin \left( x \right)+5\sin \left( y \right)$. Bạn có thể thấy độ lớn của biên độ sóng $5\sin \left( x \right)$ ở ảnh giữa và $5\sin \left( y \right)$ ở ảnh phải chiếm ưu thế trong sóng cuối
Biến đổi Fourier của ảnh sẽ tách hàm ảnh thành tổng các sóng sine tương ứng. Giống như sóng âm, biến đổi Fourier có đồ thị theo tần số còn trong ảnh thì miền tần số là 2 chiều, đó là tần số $h$ và $k$ theo chiều $x$ và $y$, do đó biến đổi Fourier có đồ thị không phải dạng chuỗi các đỉnh nhọn mà là một ảnh cùng chiều và kích thước điểm ảnh như ảnh ban đầu.
Mỗi điểm ảnh trong biến đổi Fourier có toạ độ $\left( h,k \right)$ nhằm biểu diễn sóng sine theo tần số $h$ ở trục $x$ và tần số $k$ ở trục $y$ trong biến đổi Fourier. Toạ độ tâm biểu diễn sóng $\left( 0,0 \right)$, tức một mặt phẳng không gợn sóng và cường độ (tức độ sáng của màu theo thang xám) là giá trị trung bình của các điểm ảnh trong ảnh. Điểm nằm bên trái và bên phải của điểm trung tâm biểu diễn sóng sine biến đổi theo trục $x$ (tức $k=0$). Độ sáng của những điểm này biểu diễn cường độ của sóng sine với tần số của điểm đó theo biến đổi Fourier (cường độ này là biên độ của sóng sine bình phương). Những sóng thẳng đứng ở trên và dưới điểm trung tâm biểu diễn các sóng sine thay đổi theo $y$ nhưng không đổi theo $x$ (tức $h=0$) và những điểm khác trong biến đổi Fourier biểu diễn mức đóng góp của sóng chéo.

Sóng $\sin \left( x \right)$ được biểu diễn dưới ảnh xám và biến đổi Fourier của ảnh xám đó
Ví dụ, xem ảnh bên trái, đây là ảnh xám của sóng $\sin \left( x \right)$ hai chiều, ảnh kế bên là biến đổi Fourier của ảnh xám này, ảnh biến đổi có cùng kích thước với ảnh xám, đa số là màu đen ngoại trừ những vùng sát với tâm ảnh thì có vài điểm ảnh sáng. Nếu ta phóng to vào tâm ảnh biến đổi (ảnh bên phải), bạn thấy có chính xác 3 điểm ảnh không phải màu đen, một điểm sáng nằm ở điểm tâm ảnh có toạ độ $\left( 0,0 \right)$ biểu diễn mức đóng góp của sóng $\left( 0,0 \right)$ trong ảnh, một điểm có toạ động $\left( 1,0 \right)$ và điểm đối xứng nằm ở $\left( -1,~0 \right)$ biểu diễn mức đóng góp của sóng $\left( 1,0 \right)$ (sóng sine ở ảnh trái), còn các điểm ảnh còn lại có màu đen do ảnh xám ban đầu chỉ sử dụng sóng $\left( 1,~0 \right)$.

Ảnh trên: Sóng $\sin \left( 20x \right)+\sin \left( 10y \right)$ và ảnh biến đổi Fourier cho thấy 2 cặp điểm ảnh tại toạ độ $\left( 20,0 \right)$ và $\left( 0,10 \right)$ và toạ độ đối xứng biểu diễn mức đóng góp của 2 sóng này.
Ảnh dưới: Sóng $\sin \left( 100x+50y \right)$ và ảnh biến đổi Fourier cho thấy cặp các điểm ảnh sáng tại toạ độ $\left( 100,50 \right)$ và toạ độ đối xứng
Biến đổi Fourier của các tổ hợp sóng đơn giản chỉ có vài điểm sáng, nhưng với những ảnh phức tạp hơn như ảnh kỹ thuật số thì có nhiều điểm sáng hơn khi biến đổi Fourier do ảnh dùng nhiều sóng để biểu diễn ảnh.
Biến đổi Fourier ở nhiều ảnh số mà ta thường gặp, thông thường cường độ ở trục $x$ và $y$ sẽ mạnh khi biến đổi, cho thấy các sóng sine chỉ biến đổi dọc theo các trục này có vai trò rất lớn trong ảnh cuối cùng bởi vì trong một ảnh sẽ chức rất nhiều đặc trưng theo chiều ngang và dọc và đối xứng, như ảnh chụp bức tường, cạnh bàn, kể cả cơ thể người cũng có tính đối xứng theo chiều dọc. Bạn có thể quan sát điều này bằng cách xoay ảnh một chút, khoảng $45^{o}$, khi đó biến đổi Fourier sẽ có cường độ mạnh tại cặp các đường thẳng vuông góc dã được xoay cùng một lượng với góc xoay của ảnh.

Ảnh xám trong tạp chí Plus và ảnh sau khi biến đổi Fourier cho thấy chuỗi các mức đóng góp của sóng dọc biểu diễn bởi các điểm sáng dọc theo trục tung.

Ảnh trong tạp chí Plus xoay một góc ${{45}^{o}}$ và biến đổi Fourier
Biến đổi Fourier là một công cụ tuyệt diệu khi phân tích và sử dụng âm thanh hay hình ảnh. Đối với ảnh, biến đổi Fourier là công cụ toán học quan trọng khi nén ảnh (ví dụ như chuẩn ảnh JPEG), lọc ảnh hay giảm mờ, nhiễu ảnh.
Ảnh sóng sine 2 chiều, bề mặt sóng và biến đổi Fourier được tạo bởi phần mềm toán học MATLAB, nếu bạn muốn tự trải nghiệm với ảnh của bạn, bạn có thể dùng đoạn code tại https://plus.maths.o...rola/MATLAB.TXT
Một bài tiểu luận nhỏ của tôi về lọc ảnh trong miền tần số có sử dụng đến biến đổi Fourier, sử dụng code trên MATLAB: https://www.academia..._lọc_Contourlet
Nguồn: https://plus.maths.o...ansforms-images







