Trong thế giới thực, đôi khi ta gặp những tình huống yêu cầu ta phải tối ưu hoá không gian để đạt được một ưu thế nhất định, ví dụ như sự phân nhánh và mọc lá của cây thường theo cấu trúc fractal nhằm tối đa hoá diện tích bề mặt hấp thụ nắng và các chất dinh dưỡng. Đây là một trong những nguyên do vì sao đường cong và hình dạng trong tự nhiên thường nhấp nhô, trong khi các kỹ sư thiết kế cánh máy bay hay vành xe hơi phải trơn nhằm tối ưu hoá vấn đề khác.
Ta quan sát một tình huống khác với mục tiêu là tối thiểu hoá diện tích bề mặt vào thể tích cho trước. Ví dụ, nếu ta sản xuất lon thiếc để chứa đậu xanh thì khi đó ta muốn tối thiểu diện tích thiếc gần bằng với thể tích $V$ cho trước để chứa đậu xanh. Giả sử lon có đầu và đáy hình tròn có bán kính $r$ và chiều cao $h$, khi đó tổng diện tích bề mặt (hai hình tròn có bán kính $r$ và hình trụ có đường kính $2\pi $ và chiều cao $h$) là
$$A=2\pi {{r}^{2}}+2\pi rh$$

Do thể tích lon có công thức là $V=\pi {{r}^{2}}h$, ta viết lại công thức diện tích bằng cách thay $h=V/\pi {{r}^{2}}$ như sau
$$A=2\pi {{r}^{2}}+2V/r$$
Giá trị thể tích là cố định nên để tìm diện tích nhỏ nhất của thiếc thì ta tính đạo hàm
$$\frac{dA}{dr}=4\pi r-\frac{2V}{{{r}^{2}}}$$
và cho kết quả này bằng 0 và kiểm tra bất đẳng thức ${{d}^{2}}A/d{{r}^{2}}>0$ nhằm đảm bảo kết quả nhỏ nhất là chính xác.
Do đó ta cần
$$V=2\pi {{r}^{3}}$$
mặt khác, vì $V=h\pi {{r}^{2}}$ nên ta cần $h=2r$. Từ đó ta thấy rằng trong thực tế đa số lon thiếc có chiều cao bằng với đường kính đáy.
Nếu bạn muốn làm một cái ly hình trụ thì tỉ lệ tốt nhất là $h=r$. Nếu bạn đi siêu thị và quan sát trên kệ bán hàng, bạn sẽ thấy một số lon thiếc thiết kế tối ưu với chiều cao bằng đường kính, nhưng một số lon thì không thiết kế như vậy, chắc nhà sản xuất muốn tạo nên sự khác biệt chăng?
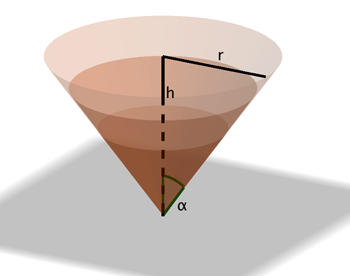
Nhân tiện, nếu ta thay đổi bài toán thành tìm hình dạng để thể tích đạt giá trị lớn nhất khi cho trước giá trị diện tích, khi đó hình dạng sẽ như thế nào? Cuối cùng, do đây là mùa hè nóng bức thích hợp để ăn kem ốc quế, hãy tự hỏi rằng khi kinh doanh, ta nên thiết kế bánh ốc quế như thế nào để kinh tế nhất. Archimedes vào thế kỷ 225 trước Công Nguyên, nếu đỉnh của một hình nón mở là hình tròn có bán kính $r$ và chiều cao đến đỉnh là $h$, khi đó thể tích cây kem bao bởi bánh hình nón là
$$V=\frac{1}{3}\pi {{r}^{2}}h$$
và diện tích bề mặt là
$$A=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$$
Bây giờ quay lại bài toán lon thiếc, ta thay $h=3V/\pi {{r}^{2}}$ vào công thức $A$, tính $dA/dr$ và chi kết quả bằng 0, ta được
$$\frac{dA}{dr}=\pi {{\left( {{r}^{2}}+\frac{9{{V}^{2}}}{{{\pi }^{2}}{{r}^{4}}} \right)}^{1/2}}+\frac{\pi r}{2}{{\left( {{r}^{2}}+\frac{9{{V}^{2}}}{{{\pi }^{2}}{{r}^{4}}} \right)}^{-\frac{1}{2}}}\left( 2r-\frac{36{{V}^{2}}}{{{\pi }^{2}}{{r}^{5}}} \right)$$
Cho biểu thức trên bằng 0, thu được kết quả là
$${{r}^{3}}=3V/\pi \sqrt{2}={{r}^{2}}h/\sqrt{2}$$
và do đó tỉ lệ tối ưu giữa chiều cao và bán kính khi thiết kế vỏ hình nón cho cây kem ốc quế là $h/r=\sqrt{2}$. Vì vậy, vì $r/h=1/\sqrt{2}$ là $\tan \left( \alpha \right)$ nên góc $\alpha ={{\tan }^{-1}}\left( 1/\sqrt{2} \right)~=0.6$ radian, tương ứng với ${{35.26}^{o}}$ hay ${{35}^{o}}15'$. Theo nghĩa nào đó thì đây là phần vỏ kem ốc quế “kinh tế” nhất.
Những vùng mờ khác nhau ở ảnh trên biểu diễn 3 cây kem ốc quế với thể tích khác nhau, nhưng mỗi cây kem có giá trị $\alpha $ nhằm đảm bảo diện tích bề mặt nhỏ nhất ứng với thể tích tương ứng.
Nguồn: https://plus.maths.o...ent/outer-space







