Đề thi chọn đội tuyển Học sinh giỏi môn Toán tỉnh Thanh Hóa năm 2017 - 2018
Bài 1. Cho dãy số: $a_{0}, a_{1}, a_{2}, ...$ thỏa mãn: $a_{m+n}+a_{m-n}=\frac{1}{2}\left ( a_{2m}+a_{2n} \right ),$ với mọi số nguyên không âm $m, n$ và $m\geq n.$ Nếu $a_{1}=1,$ hãy xác định: $a_{2017}.$
Bài 2. Tìm tất cả các hàm số $f:\mathbb{R}\rightarrow \mathbb{R}$ thỏa mãn: $f(n^{2})=f(n+m).f(n-m)+m^{2}, \forall m, n\in \mathbb{R}.$
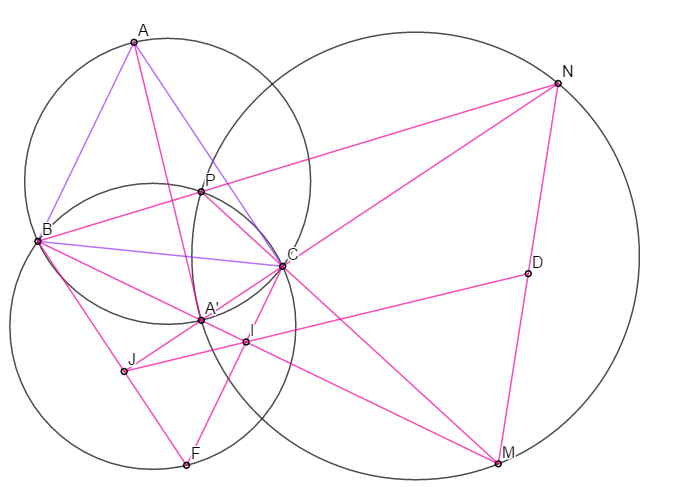
Bài 3. Tam giác $ABC$ nhọn có $H$ là trực tâm và $P$ là điểm di động bên trong tam giác sao cho $\widehat{BPC}=\widehat{BHC}.$ Đường thẳng qua $B$ và vuông góc với $AB$ cắt $PC$ tại $M,$ đường thẳng qua $C$ và vuông góc với $AC$ cắt $PB$ tại $N.$ Chứng minh rằng: trung điểm $I$ của $MN$ luôn thuộc một đường thẳng cố định.
Bài 4. Tìm tất cả các đa thức $P(x)$ có các hệ số nguyên thỏa mãn $P(2017)=1,$ $3^{n}-1$ chia hết cho $P(n)$ với mọi số nguyên dương $n.$
Bài 5. Chứng minh rằng: $\sum_{k=0}^{n}2^{k}C_{n}^{k}C_{n-k}^{\left [ \frac{n-k}{2} \right ]}=C_{2n+1}^{n}.$
*Đề thi có tham khảo ở link sau: http://olympictoanho...-2017-2018.html