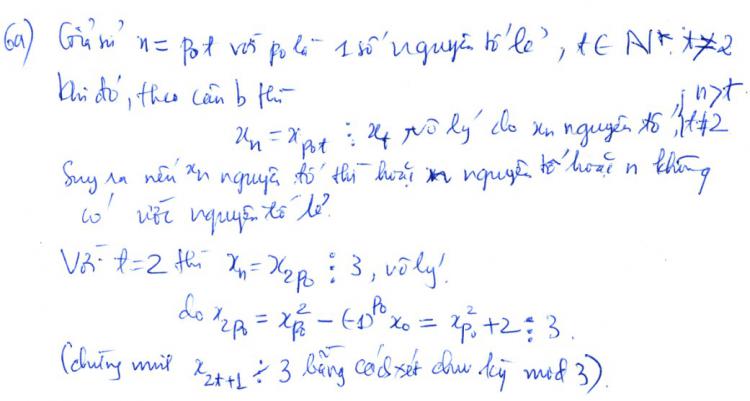Chủ đề này có 49 trả lời

[Dinh Xuan Hung]

[anhquannbk]

Câu 6b là một tính chất của dãy $Lucas   (L_n)$

Với $m$ là số lẻ, ta có:

$ L_{mn} \vdots L_n$

 Câu a là hệ quả của tính chất này.

Bài viết đã được chỉnh sửa nội dung bởi anhquannbk: 12-01-2018 - 12:01

[Duy Thai2002]

Câu 6 a) CTTQ của dãy:

$x_{n}=(\frac{1+\sqrt{5}}{2})^{n}+(\frac{1-\sqrt{5}}{2})^{n}=a^{n}+b^{n}$ với $\left\{\begin{matrix}a=\frac{1+\sqrt{5}}{2} & \\b=\frac{1-\sqrt{5}}{2} & \end{matrix}\right.$

Dễ dàng chứng minh dãy $x_{n}$ nguyên

$=> a^{n}+b^{n}$ nguyên

Ta sử dụng tính chất sau:

$a^{n}+b^{n}$ nguyên $\forall n\in \mathbb{N}$, c lẻ

$=> a^{c}+b^{c}\vdots a+b$ 

CM: Sử dụng phân tích $a^{n}+b^{n}=(a+b)...$

Quay lại bài toán ta  sử dụng phản chứng 

Giả sử $x_{n}$ nguyên tố nhưng n là hợp số có ước nguyên tố lẻ, giả sử n=x.y, trong đó x lẻ

$=> x_{n}=(a^{y})^{x}+(b^{y})^{x}\vdots a^{y}+b^{y}$

$=> x_{n}$ là  hợp số ( Mâu thuẫn với gt)

=> Đpcm.

Ở đây bỏ qua TH n=0

b) Câu  b là tính chất của dãy Lucas.

Bài viết đã được chỉnh sửa nội dung bởi Duy Thai2002: 12-01-2018 - 12:29

[tranquocluat_ht]

26230865_199457050617859_3577639234407324133_n.jpg

 

Câu a có thể tiếp cận như sau

Hình gửi kèm

• 
• 

Bài viết đã được chỉnh sửa nội dung bởi tranquocluat_ht: 12-01-2018 - 22:55

[tranquocluat_ht]

26230865_199457050617859_3577639234407324133_n.jpg

Câu 6 có thể làm như sau

Hình gửi kèm

• 
• 
• 

Bài viết đã được chỉnh sửa nội dung bởi tranquocluat_ht: 13-01-2018 - 13:53

[AnhTran2911]

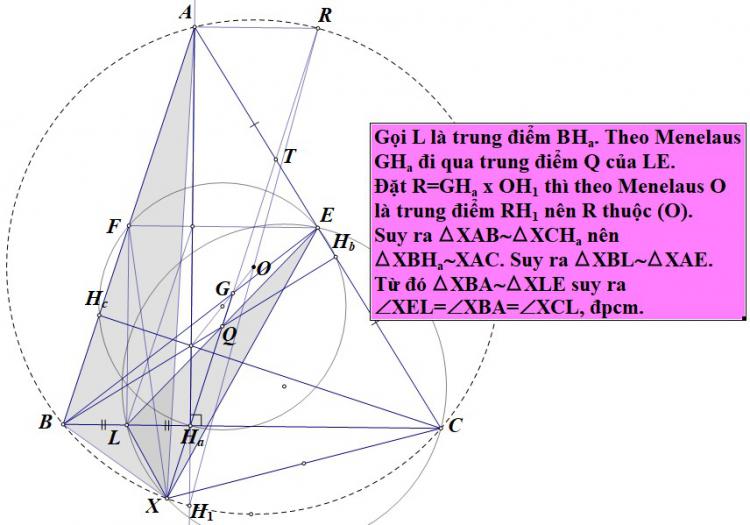
Cấu hình bài toán 7a rất quen thuộc Với điểm $X$ đã xác định một cách khá rõ ràng

Qua $A$ vẽ $AP\parallel{BC}$ ( $P \in(O)$). Vì tứ giác $APCB$ là hình thang cân mà $AH_{a}$ vuông góc $BC$ , $D$ trung điểm BC nên $AP=2MH_{a}$. Do đó $AP$ cắt $OH$ tại trọng tâm $G$ của tam giác $ABC$ . Vì vậy $P,X,H_{a}$ thẳng hàng.

Lại có $\angle{BH_{a}X}=\angle{PH_{a}C}=\angle{ACX}$ . Suy ra $\triangle{ABC}\sim{\triangle{ACX}}$. Gọi $K$ là trung điểm $BH_{a}$ thì $\triangle{XH_{a}K}\sim{\triangle{XCE}}$

Suy ra góc $\angle{KXE}=\angle{PXC}=\angle{KCE}$ . Do đó bốn điểm $K, X, C ,E$ đồng viên ( đpcm)

Câu b có thể suy nghĩ theo hướng Ceva kết hợp Mênêlaus song Trục đẳng phương va phương tích vẫn tỏ ra hiệu quả trong bài toán này

Thực ra bài hình 7 VMO năm nay cũng có nhiều đặc điểm tương tự như tính chất như bài hình ngày 1 của kì thi $VNTST$ năm 2009

 

Bài viết đã được chỉnh sửa nội dung bởi AnhTran2911: 12-01-2018 - 16:12

[Duy Thai2002]

Câu 5a làm không biết đúng không, mong mọi người chỉ bảo

Nhận thấy tập $S_{3}(5)$ phải nhận ba giá trị vì nếu nhân có hai giá trị thì có thê là một trong các trường hợp sau:

$\begin{bmatrix}{1;2;1;2;1} & \\ {2;1;2;1;2} & \end{bmatrix}$ ( vô lý theo iii)

Giả sử $x_{1}=1$

$=> \begin{bmatrix}x_{2}=3 & \\x_{2}=2 & \end{bmatrix}$

Giả sử luôn $x_{2}=2$

Nếu $x_{3}=1$, khi đó $\begin{bmatrix}x_{4}=2 & \\ x_{5}=2 & \end{bmatrix}$ ( điều vô lý theo iii)

$\begin{bmatrix}x_{4}=3,x_{5}=1

$=> S_{3}(5)={1;2;1;3;1}$

$=> x_{3}=3$

$=> x_{4},x_{5}$ sẽ nhận một trong ba giá trị :1 hoặc 2 hoặc 3 

Nhận thấy để $x_{i}=3$ thì $i=5$

$=>\begin{bmatrix}x_{4}=2 & \\x_{4}=1 & \end{bmatrix}$ (Trường hợp trên không thể xảy ra vì mâu thuẫn với iii)

Nếu $x_{4}=1$ $=> x_{5}=2$ $=> S_{3}(5)={1;2;3;1;2}$ (loại)

$=> x_{4}=2=> x_{5}=1=> S_{3}(5)={1;2;3;2;1}$ (nhận)

Mà do tính hoán vị của 1;2;3 nên có thêm $3!$ cách

Vậy số phần tử của tập hợp là $2.3!$

Bài viết đã được chỉnh sửa nội dung bởi Duy Thai2002: 13-01-2018 - 07:59

[manht1k23]

Câu 4a làm không biết đúng không, mong mọi người chỉ bảo

Nhận thấy tập $S_{3}(5)$ phải nhận ba giá trị vì nếu nhân có hai giá trị thì có thê là một trong các trường hợp sau:

$\begin{bmatrix}{1;2;1;2;1} & \\ {2;1;2;1;2} & \end{bmatrix}$ ( vô lý theo iii)

Giả sử $x_{1}=1$

$=> \begin{bmatrix}x_{2}=3 & \\x_{2}=2 & \end{bmatrix}$

Giả sử luôn $x_{2}=2$

Nếu $x_{3}=1$, khi đó $\begin{bmatrix}x_{4}=2 & \\ x_{5}=2 & \end{bmatrix}$ ( điều vô lý theo iii)

$=> x_{3}=3$

$=> x_{4},x_{5}$ sẽ nhận một trong ba giá trị :1 hoặc 2 hoặc 3 

Nhận thấy để $x_{i}=3$ thì $i=5$

$=>\begin{bmatrix}x_{4}=2 & \\x_{4}=1 & \end{bmatrix}$ (Trường hợp trên không thể xảy ra vì mâu thuẫn với iii)

Nếu $x_{4}=1$ $=> x_{5}=2$ $=> S_{3}(5)={1;2;3;1;2}$ (loại)

$=> x_{4}=2=> x_{5}=1=> S_{3}(5)={1;2;3;2;1}$ (nhận)

Vậy số phần tử của tập hợp là 5 với 1 cách sắp xếp là:{1;2;3;2;1}

ngoài 12321 còn có 12131, và phải nhân thêm 3! cách hoán vị vai trò các số 1, 2, 3 nữa, đáp số bài này là 12

[IHateMath]

Mình có ý tưởng cho câu b bài 5, đã đăng lên bên AOPS. Xin đăng lại ở đây; bạn đọc kiểm tra dùm.

Trước hết ta nhận thấy rằng nếu $d=2n-1$ thì tồn tại một bộ số như vậy:

$$n,n-1,n-2,\dots ,3,2,1,2,3,\dots ,n-2,n-1,n$$

Để hoàn tất chứng minh, ta chỉ ra rằng với mỗi $d$ nguyên dương, số $n$ nhỏ nhất sao cho $|S_n(d)|>0$ thì không nhỏ hơn $\frac{d+1}{2}$, bằng quy nạp.

Trường hợp $d=1$ hiển nhiên đúng.

Giả sử $k+1$ là số nguyên dương nhỏ nhất mà mệnh đề trên sai. Khi đó tồn tại một bộ $k+1$-số sao cho $n< \frac{k+2}{2}$. Khi đó phải tồn tại hai chỉ số $i,j$ sao cho $x_i=x_j$ và $|i-j|$ nhỏ nhất có thể. Khi đó mọi số nguyên nằm giữa $x_i,x_j$ chỉ xuất hiện đúng một lần, suy ra phải có một số $m$ nào đó xuất hiện ba lần. Ta thấy rằng bộ $k+1$-số bị cắt thành bốn đoạn (có thể rỗng) bởi $m$:

$$\{S_1\}m\{S_2\}m\{S_3\}m\{S_4\}$$

Gọi $\ell_i$ là độ dài của $S_i$. Khi đó theo giả thiết quy nạp, đoạn này rỗng hoặc chứa ít nhất $v_i\geq \frac{\ell_i+1}{2}$ giá trị phân biệt. ta có các trường hợp sau:

$\bullet\quad S_1\cap S_4=\varnothing$. Khi đó có ít nhất$$\frac{1}{2}\sum_{i:S_i\ne\varnothing}{(\ell_i+1)}\geq\frac{1}{2}\left(\left(\sum_{i:S_i\ne\varnothing}{\ell_i}\right)+2\right)=\frac{1}{2}(k-2+2)>n-1$$giá trị phân biệt khác $b$, mâu thuẫn.

$\bullet\quad S_1\cap S_4\ne\varnothing$. Nếu ta nối $S_1,b,S_4$ để tạo thành một đoạn $k-\ell_2-\ell_3-1$ thì đoạn này phải có ít nhất $\frac{1}{2}(k-\ell_2-\ell_3)$ giá trị phân biệt. Do đó có tối thiểu$$\frac{1}{2}(\ell_2+\ell_3+2+k-\ell_2-\ell_3)=\frac{k+2}{2}>n$$giá trị phân biệt khác $b$, cũng vô lý nốt.

P/s: Chợt nhận ra mình làm quá tay, chỉ đơn giản thế này thôi.

Giả sử $k+1$ là số nguyên dương nhỏ nhất mà mệnh đề trên sai. Khi đó tồn tại một bộ $k+1$-số sao cho $n< \frac{k+2}{2}$. Nếu $k$ chẵn thì $n\leq \frac{k}{2}$, vô lý. Nếu $k$ lẻ thì $n\leq\frac{k+1}{2}$. Theo giả thiết quy nạp, từ $x_1$ tới $x_k$ có $\frac{k+1}{2}$ giá trị phân biệt, suy ra tồn tại $i\in\{1,2,\dots ,k-1\}$ sao cho $x_i=x_{k+1}$. Cũng theo giả thiết quy nạp, từ $x_1$ đến $x_{i-1}$ có $\frac{i}{2}$ giá trị phân biệt, trong khi từ $x_{i+1}$ đến $x_k$ có $\frac{k-i}{2}$. Mặt khác, $\{x_1,x_2,\dots ,x_{i-1}\}\cap\{x_{i+1},x_{i+2},\dots ,x_k\}=\varnothing$, suy ra dãy có $\lceil\frac{i+k-i}{2}\rceil=\frac{k+1}{2}$ giá trị phân biệt không kể đến $x_i,x_{k+1}$, vô lý.

Bài viết đã được chỉnh sửa nội dung bởi IHateMath: 13-01-2018 - 15:33

[dauga]

Bài 1:

Từ các điều kiện của bài toán dễ dàng đoán ngay giới hạn của dãy là $1$. Từ đó ý tưởng là đặt dãy $y_n = x_n - 1$. Ta cần chứng minh dãy này có giới hạn là $0$ và với mọi $n\ge 0$ thì  $0\le y_1 + y_2 + \cdots + y_n \le 1$.

Ta có $x_{n+1} - 1 = \sqrt{x_n + 8} - 3 - (\sqrt{x_n + 3} - 2) = \frac{x_n-1}{\sqrt{x_n+8} + 3} - \frac{x_n-1}{\sqrt{x_n+3} + 2}$

nên công thức truy hồi của $y_n$ là $y_1 = 1$ và $y_{n+1} = y_n\left(\frac{1}{\sqrt{y_n + 9} + 3} - \frac{1}{\sqrt{y_n+4}+2}\right)$ với mọi $n\ge 1$.

Dễ thấy $\left|\frac{1}{\sqrt{y_n + 9} + 3} - \frac{1}{\sqrt{y_n+4}+2}\right| \le \frac{1}{2}$. Nên ta có $|y_{n+1}| \le \frac{1}{2}|y_n|$ với mọi $n\ge 1$. Do đó dãy $|y_n|$ có giới hạn là $0$. Hệ quả là giới hạn của $x_n$ là $1$ $\square$

Từ $\frac{1}{\sqrt{y_n + 9} + 3} - \frac{1}{\sqrt{y_n+4}+2} < 0$  trên thì ta có $y_n$ luôn phiên đổi dấu. Mà $y_1 = 1 > 0$ nên $y_k \ge 0$ với $k$ lẻ và $y_k \le 0$ với $k$ chẵn. Lại có $|y_{k+1}| \le |y_k|$ nên ta có $y_{2t+1}\le -y_{2t} \le y_{2t-1}$ với mọi $t\ge 1$. Hay $y_{2t} + y_{2t-1} \ge 0$ và $y_{2t} + y_{2t+1}\le 0$ với mọi $t \ge 1$.

Dó với mọi $k$ thì $y_1 + y_2 + \cdots + y_{2k} = (y_1 + y_2) +
\cdots + (y_{2k-1} + y_{2k}) \ge 0$. Vì $y_{2k+1} \ge 0$ nên cũng phải có $y_1 + y_2 + \cdots + y_{2k+1} \ge 0$.

Tương tự $y_1 + y_2 + \cdots + y_{2k-1} = y_1 + (y_2+y_3) + \cdots + (y_{2k-2} + y_{2k-1}) + y_{2k} \le 1$. Vì $y_{2k} \le 0$ nên cũng phải có $y_1 + y_2 + \cdots + y_{2k} \le 1$

$\blacksquare$

Bài 5.

a. Dễ thấy vai trò của $1, 2, 3$ là như nhau nên có thể giả sử $x_1 = 1$, $x_2 = 2$. Xét hai trường hợp, $x_3 = 1$ và $x_3 = 3$.

Nếu $x_3 = 1$ thì từ điều kiện 2. ta có $x_4, x_5$ đều khác 2. Mà $x_4$ phải khác 1 nên $x_4 = 3$. Do đó $x_5 = 1$. Dãy $1,2,1,3,1$ thỏa mãn cả hai điều kiện.

Nếu $x_3 = 3$ thì $x_4 = 1$ hoặc $2$. Nếu $x_4 = 1$ thì $x_5$ không thể là $1$ (điều kiện 1), hay $2$ và $3$ (điều kiện 2). Do đó $x_4 = 2$, khi đó dễ thấy chỉ còn có $x_5 = 1$. Ta thu được dãy $1,2,3,2,1$.

Vậy tổng cộng sẽ có $S_3(5) = 3!\times 2 = 12$ dãy thỏa mãn.

b. Ta chứng minh bằng quy nạp với mỗi $n$ thì  mọi dãy có độ dài $2n$ bất kì đều không thỏa mãn ít nhất một trong các điều kiện của bài toán bằng quy nạp.

Thật vậy với $n=1$ thì dãy có độ dài $2$ sẽ phạm vào điều kiện 1. Giả sử đã đúng tới $n-1\ge 1$. Xét với $n$. Giả sử tồn tại dãy $x_1,...,x_{2n}$ thỏa mãn các điều kiện đề bài. Nếu có số $a$ chỉ xuất hiện $1$ lần trong dãy, thì khi bỏ phần tử $a$ đi, thì ta có dãy mới gồm $2n-1$ phần tử và vẫn thỏa mãn điều kiện. Nhưng điều này mâu thuẫn với giải thiết quy nạp. Vậy mỗi số nếu xuất hiện trong dãy thì sẽ xuất hiện 2 lân. Do đó mỗi $1\le i\le n$ sẽ có hai chỉ số $t_i < l_i$ mà $x_{t_i} = x_{l_i} = i$. Không mất tính tổng quát, giả sử $t_1 < t_2 < \cdots < t_n$ thì theo điều kiện 2, phải có $l_1 > l_2 > \cdots > l_n > t_n$. Nhưng khi đó thì sẽ phải có $t_n = n$, $l_n = n+1$ và điều này mâu thuẫn với điều kiện 1. Vậy không có dãy nào có độ dài $2n$ nào thỏa mãn cả hai điều kiện. ĐPCM.

Với $d=2n-1$ thì dễ thấy dãy $1,2,...,n-1,n,n-1,..,1$ thỏa mãn. Và hiển nhiên nếu dãy độ dài $d$ thỏa mãn thì chỉ cần bỏ đi một phần tử bất kì, ta thu được dãy có độ dài $d-1$ thỏa mãn. Câu b. được chứng minh hoàn toàn.

 

Bài 6:

Gọi dãy Fibonacci như sau: $F_{-2} = 1, F_{-1} = 0, F_0 = 1, F_1 = 1$ và $F_{n+1} = F_{n} + F_{n-1}$ với mọi $n \ge 0$.


Ta gọi một dãy $x_n$ có tính "Fibo" nếu nó thỏa mãn hệ thức truy hồi $a_{n+1} = a_{n} + a_{n-1}$ với mọi $n\ge 1$.

Bổ đề 1: Ta có tính chất sau cho dãy "Fibo":

$a_{m} = F_{k}a_{m-k} + F_{k-1}a_{m-k-1}$.

Chứng minh:

Thật vậy $a_{m} = a_{m-1} + a_{m-2} = F_1a_{m-1} + F_{0}a_{m-2}$. Nên điều trên đúng với $k=1$. Giả sử đã đúng tới $k$. Tức $a_{m} = F_{k}a_{m-k} + F_{k-1}a_{m-k-1}$, thì có

$a_{m} = F_{k}(a_{m-k-1} + a_{m-k-2}) + F_{k-1}a_{m-k-1}$

$ = (F_{k} + F_{k-1})a_{m-k-1} + F_{k}a_{m-k-2}$

$= F_{k+1}a_{m-k-1} + F_{k}a_{m-k-2}$ $\square$.

Ta có $x_0 = 2 = F_{0} + F_{-2}$, $x_1 = 1 = F_{1} + F_{-1}$, nên dễ thấy $x_{n} = F_{n} + F_{n-2}$.

Bổ đề 2:
Với mọi $n\ge 2$ thì $x_{n} | F_{2n-1}$ và $\text{gcd}(x_n, F_{2n}) = 1$.

Chứng minh:
Ta có dãy Fibonacci có tính chất "Fibo" nên theo bổ đề 1 ta có

$F_{2n-1} = F_{n}F_{n-1} + F_{n-1}F_{n-2} = (F_{n} + F_{n-2})F_{n-1} = x_nF_{n-1}$, do đó $a_{n} | F_{2n-1}$ với mọi $n$.

Lại dễ thấy $\text{gcd}(F_{k},F_{k-1}) = \text{gcd}(F_{k-1},F_{k-2}) = ...=\text{gcd}(F_{1}, F{0}) = 1$ với mọi $k\ge 0$ nên hệ quả là $\text{gcd}(F_{2n}, F_{2n-1}) = 1$. Mà $x_n |  F_{2n-1}$ và với $n\ge 2$ thì $x_{n} \ge 2$ nên phải có $\text{gcd}(x_n, F_{2n}) = 1$ $\square$

Xét số $m \neq 2$. Dãy $x_k$ tăng ngặt với $k\ge 2$ nên $x_k < x_{m}$ với mọi $0\le k < m$. Do đó $x_n$ không chia hết cho $x_m$ với mọi $ m < n$.

Với $m < n \le 2m$ thì theo bổ đề 1 ta có

$x_{n} = F_{n-m}x_{m} + F_{n-m-1}x_{m-1}$, có $\text{gcd}(x_m, x_{m-1}) = 1$ nên ta có nếu $x_m$ chia hết cho $x_m$ thì phải có $F_{n-m-1}$ chia hết cho $x_m$. Tuy nhiên $0 < F_{n-m-1} \le F_{n-1} < x_{n}$ nên điều này không xảy ra. Vậy $x_n$ không chia hết cho $x_m$ với mọi $m < n \le 2m$.

Xét với $n > 2m$ ta có

$x_{n} = F_{2m}x_{n-2m} + F_{2m-1}x_{n-2m-1}$

Theo bổ đề 2 thì $F_{2m-1}$ chia hết cho $x_m$ và $\text{gcd}(F_{2m}, x_m) = 1$ nên $x_n$ chia hết cho $x_m$ khi và chỉ khi $x_{n-2m}$ chia hết cho $x_m$. Đặt $n = 2mt + r$ với $0\le r < 2m$ thì dễ dàng có $x_n$ chia hết cho $x_m$ khi và chỉ khi $x_r$ chia hết cho $x_m$. Điều này chỉ xảy ra khi và chỉ khi $r = m$ hay $n = (2t+1)m$.

Vậy với mọi $m\ge 2$ thì $x_n$ chia hết cho $x_m$ khi và chỉ khi $n = (2t+1)m$.

Xét $m=1$ thì $x_m = 1$ nên $x_n$ chia hết cho $x_m$ với mọi $n$.

Xét $m=0$ thì khi xét module $2$ thì dễ tuần với với chu kì là $3$ là $0, 1, 1$. Do đó $x_n$ chia hết cho $x_0$ khi và chỉ khi $n = 3t$.

Vậy đáp số của câu b. là $(m, n) = (1, t)$ hoặc $(0, 3t)$ hoặc $(a, (2t+1)a)$ với mọi $t, a$$\square$

Trở lại câu a. Giả sử $n$ là hợp số và có ước nguyên tố lẻ $p$. Theo trên ta có $x_n$ chia hết cho $x_{n/p}$  và $x_n > x_{n/p}$ nên $x_n$ không thể là số nguyên tố. Do đó nếu $x_n$ là số nguyên tố thì $n$ là số nguyên tố hoặc $n$ không có ước nguyên tố lẻ $\square$.
 

File gửi kèm

•  vmo2018.pdf   135.2K   345 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi dauga: 13-01-2018 - 04:09

[Duy Thai2002]

Câu 5b

Đây là cách làm của một bạn bên aops. Xin trích dẫn cách làm của bạn:

 

 

Let n points in a line colored with d colors.Those points satisfied that every segment connected 2 points with the same color would not have the common point with the other segment connected 2 points with the same color or it would content the 2 segment connected others with the same color.Show that n is maximumly equal to 2d-1.

Cho n điểm nằm trên một đương thẳng được tô bởi d màu. Những điểm này phải thoả sao cho mỗi đoạn thẳng nối hai điểm cùng màu sẽ không có điểm chung với những đoạn thẳng khác cũng nối hai điểm cùng màu hoặc nó thoả hai đoạn thẳng nối những điểm khác với cùng màu. Do đó,  n  không vượt  quá 2d-1.

P/s: Trình độ tiếng anh hạn chế nne6nmong mọi người chỉ bảo.

[Zeref]

Một hướng tiếp cận bài hình ngày 2 ở câu a không dùng biến đổi góc

Ta có bổ đề: Cho hình thang cân $ABCD$, trọng tâm của $\Delta ABC$ là $G$, hình chiếu của $A$ xuống $BC$ là $E$. Lúc đó $\overline{D,G,E}$ 

Áp dụng bổ đề, kéo dài tia $H_aG$ cắt $(O)$ tại $R$.  $\Rightarrow AR \parallel BC \Rightarrow \angle CH_aG=\angle ARX=\angle ACX \Rightarrow \angle GXC = \angle ACB = \angle AXB$
Từ đó ta dễ suy ra $\Delta XBH_a \sim XAC \Rightarrow \Delta XMH_a \sim \Delta XEC \Rightarrow \angle MXE = \angle GXC = \angle ACB$. Vậy $M,E,C,X$ đồng viên

 

[Uchiha sisui]

 

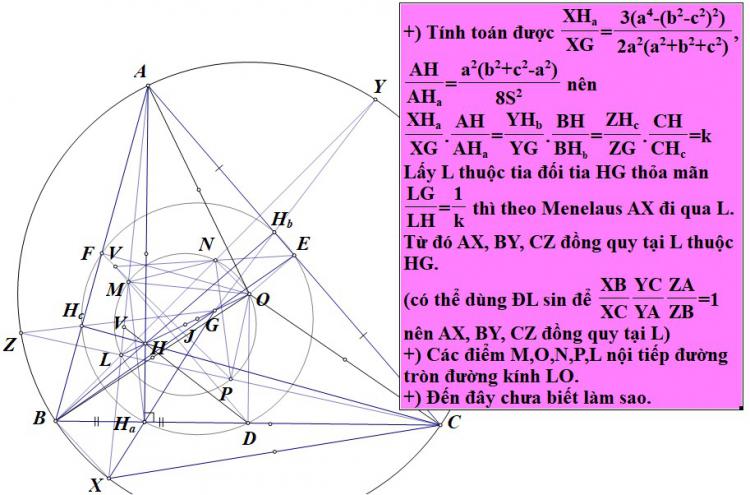
Một hướng tiếp cận bài hình ngày 2 ở câu a không dùng biến đổi góc

Ta có bổ đề: Cho hình thang cân $ABCD$, trọng tâm của $\Delta ABC$ là $G$, hình chiếu của $A$ xuống $BC$ là $E$. Lúc đó $\overline{D,G,E}$ 

Áp dụng bổ đề, kéo dài tia $H_aG$ cắt $(O)$ tại $R$.  $\Rightarrow AR \parallel BC \Rightarrow \angle CH_aG=\angle ARX=\angle ACX \Rightarrow \angle GXC = \angle ACB = \angle AXB$
Từ đó ta dễ suy ra $\Delta XBH_a \sim XAC \Rightarrow \Delta XMH_a \sim \Delta XEC \Rightarrow \angle MXE = \angle GXC = \angle ACB$. Vậy $M,E,C,X$ đồng viên

 

 

Cho em hỏi bổ đề mà anh nêu chứng minh thế nào ạ

[Tsukuyo Inaba]

Hướng giải 6b như thế này:

Trước hết phải có đẳng thức này:$ ac+bd= (a+b)(c+d) -(ad+bc)$

Xét  trường hợp sau

+)$m=kn$ (k lẻ)

Cái này là câu a nên ta ko bàn nữa

+)$m=2kn+r$

Sử dụng đẳng thức như vừa viết ta lùi về đươc về $a_{n-r}$ chia hết cho $a_{n}$ (ko xảy ra)

+)$m=kn+r$

Sử dụng đẳng thức như trên ta được $a_r$ chia hết cho$ a_n$ ( không xảy ra)....

Như vậy $m=kn$ với $k$ lẻ.

Có lẽ mình quên những trường hợp ban đầu có gì các bạn tự sửa cho.

Bài viết đã được chỉnh sửa nội dung bởi Tsukuyo Inaba: 19-01-2018 - 21:12
Latex

[Little Boy]

Lấy H,G,O. AH cắt đường tròn tại L. Kẻ đk LK của (O). Dùng đl Menelaus suy ra E,G,K thẳng hàng

Bài viết đã được chỉnh sửa nội dung bởi Little Boy: 15-01-2018 - 21:17

[Leminhthuc]

Cho minh hoi khi nao co ket qua VMO 2018 vay? Cam on nhieu

[Zz Isaac Newton Zz]

Kết quả VMO 2018, diễn đàn ta có ai đoạt giải vô điểm danh nào: https://drive.google...j3kPpHX8DO/view

[toanhoc2017]

Có ds vmo 2018 chưa pạn

[chungvinsofts]

Khó quá làm mãi mới được bài....

[Jinbei]

Phân định giải : https://bigschool.vn...a-thpt-nam-2018