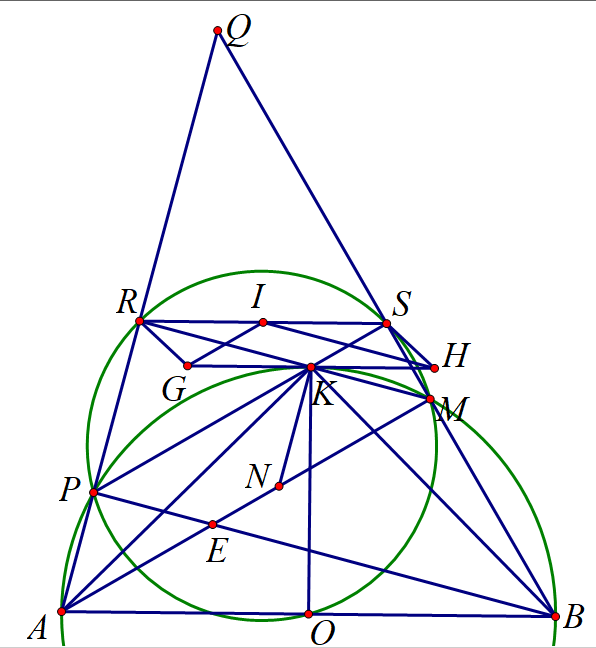
1. tứ giác $PQME$ nội tiếp đường tròn đường kính $QE$.
2. Có - $\angle KAN = \angle KBM;AN = MB;AK =BK \Rightarrow \Delta AKN = \Delta BKM(c.g.c)$
3. $\angle MBP = 180^o - \angle KMB = 45^o$ lại có $PQ \perp PB \Rightarrow \Delta PQB$ vuông cân.
hơn nữa $\\angle PQB = \angle PBA = 45^o \Rightarrow \angle KBM = \angle PBA \Rightarrow PKMA$ là hình thang cân.
lại có $MQ \perp AM \Rightarrow \Delta QMA$ vuông cân. $\Rightarrow \Delta MQE \sim \Delta MQA(g.g) \Rightarrow \frac{MB}{MA} = \frac{EB}{QA} \Rightarrow AQ.BM = BE.AM.$ mà $BE = AN$ $\Rightarrow AN.AQ = BE.AM$.
4. Gọi $ G$ và $H$ là hai điểm trên đường vuông góc với $KO$ tại $K$ sao cho $K$ là trung điểm của $GH$.
$HG = R$ có $MA // PB$ mà $PB \perp QA$ nên $MK // QA \Rightarrow R,K,M$ thẳng hàng. tương tự, $P,K,S$ thẳng hàng
$\Rightarrow RS = \frac{1}{2}AB = R \Rightarrow RSHG$ là hình bình hành. $GI //KS ; HI//GK \Rightarrow \angle GIM = \angle GKS = 180^o - \angle AQB = 135^o$.
Góc $GIH$ luôn nhìn $GH$ một góc cố định mà $HG$ cố định nên $I$ chạy trên cung chứa góc $135^o$ dựng trên $GH$.
Bài viết đã được chỉnh sửa nội dung bởi Minhcamgia: 25-03-2018 - 08:26
![]()
![]()