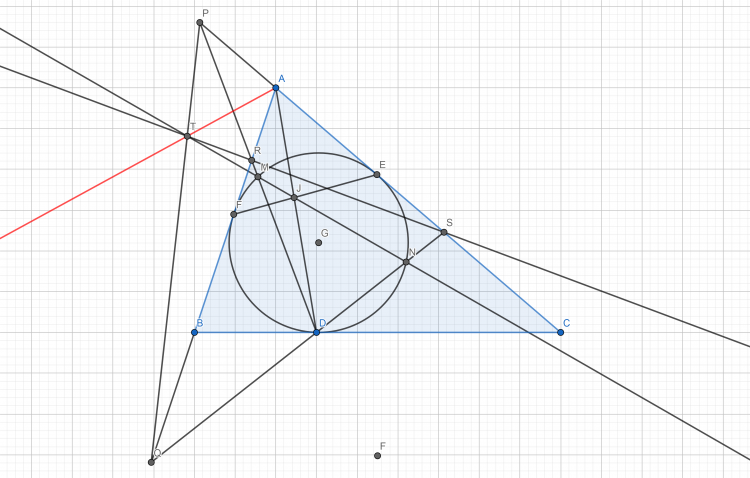
Đường tròn $(I)$ nội tiếp tam giác $ABC$ tiếp xúc với $BC,CA,AB$ lần lượt tại $D,E,F$. $AD$ cắt $EF$ tại $J$. Một đường thẳng $d$ thay đổi qua $J$ cắt $(I)$ tại $M,N$($M$ và $C$ cùng phía so với $AD$), $DM$ cắt $AC,AB$ lần lượt tại $P,R$. $DN$ cắt $AB,AC$ lần lượt tại $Q,S$.
Chứng minh: $MN,PQ,RS$ đồng quy tại một điểm $T$ và khi $d$ thay đổi quanh $J$ thì $T$ luôn thuộc một đường thẳng cố định.