Đề thi vào 10 chuyên Lê Hồng Phong - Nam Định 2018 - 2019
Môn thi: Toán Chuyên
Ngày thi 26/5/2018
Thời gian 120 phút
Câu 1 (2 điểm)
a) Rút gọn biểu thức $P=\frac{x^2}{(x+y)(1-y)}-\frac{y^2}{(x+y)(1+x)}-\frac{x^2y^2}{(1+x)(1-y)}$
b) Chứng minh rằng: $\sqrt{1+\frac{1}{1^2}+\frac{1}{2^2}}+\sqrt{1+\frac{1}{2^2}+\frac{1}{3^2}}+...+\sqrt{1+\frac{1}{2017^2}+\frac{1}{2018^2}}<2018$
Câu 2 (2 điểm)
a) giải PT: $2((1-x)\sqrt{x^2+2x-1}+x)=x^2-1$
b) giải hệ phương trình: $\left\{\begin{matrix} x-3y-2+\sqrt{y(x-y-1)+x}=0 & & \\ 3\sqrt{8-x}-\frac{4y}{\sqrt{y+1}+1}=x^2-14y-8 & & \end{matrix}\right.$
Câu 3 (3 điểm)
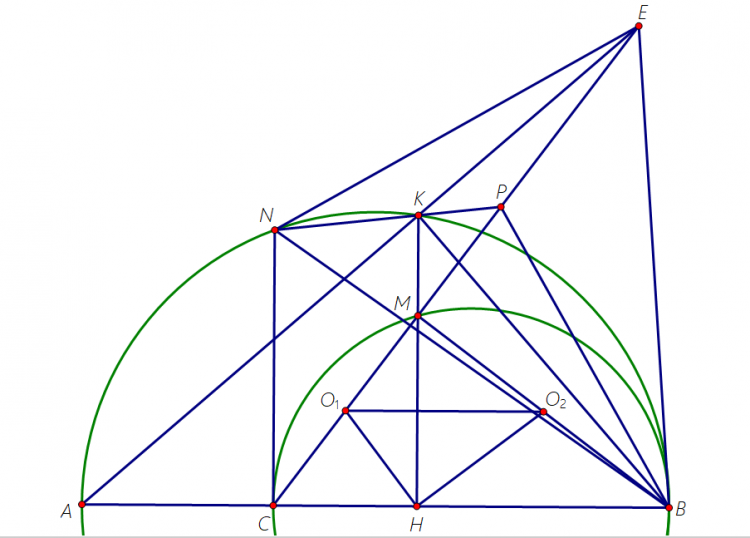
Cho đoạn thẳng AB và C là điểm nằm giữa hai điểm $A,B$. Trên cùng một nửa mặt phẳng bờ là đường thẳng $AB$, vẽ nửa đường tròn đường kính $AB$ và nửa đường tròn đường kính $BC$. Lấy điểm $M$ thuộc nửa đường tròn đường kính $BC$ ( M khác B, C). Kẻ MH vuông góc với BC ( $H \in BC$), đường thẳng MH cắt nửa đường tròn đường kính AB tại K. Hai đường thẳng AK, CM giao nhau tại E
a) Chứng minh $BE^2=BC.AB$
b) Từ C kẻ CN vuông góc với AB ( N thuộc nửa đường tròn đường kính AB), Gọi P là giao điểm của NK và CE. Chứng minh rằng tâm đường tròn nội tiếp của các tam giác $BNE$ và $PNE$ cùng nằm trên đường $BP$
c) Cho $BC=2R$. Gọi $O_1;O_2$ lần lượt là tâm đường tròn nội tiếp các tam giác $MCH$ và $MBH$. xác định vị trí điểm $M$ để chu vi tam giác $O_1HO_2$ lớn nhất
Câu 4 ( 1,5 điểm)
a) Tìm tất cả các cặp số nguyên $(x;y)$ thỏa mãn $2x^2+5y^2=41+2xy$
b) Có bao nhiêu số tự nhiên $n$ không vượt quá $2019$ thỏa mãn $n^3+2019$ chia hết cho 6
Câu 5 (1.5 điểm)
a) Cho các số thực dương thỏa mãn $\sqrt{a}+\sqrt{b}=1$
Chứng minh rằng $3(a+b)^2-(a+b)+4ab \geq \frac{1}{2}\sqrt{(a+3b)(b+3a)}$
b) Cho 100 điểm trên mặt phẳng sao trong trong bất kỳ 4 điểm nào cũng có ít nhất 3 điểm thẳng hàng. Chứng minh rằng ta có thể bỏ đi một điểm trong 100 điểm đó để 99 điểm còn lại cùng thuộc 1 đường thẳng
Bài viết đã được chỉnh sửa nội dung bởi trambau: 27-05-2018 - 10:27