Đề thi tuyển sinh vào lớp 10 THPT chuyên tỉnh Bắc Ninh năm học 2018-2019
#1
 Đã gửi 04-06-2018 - 21:09
Đã gửi 04-06-2018 - 21:09

#2
 Đã gửi 04-06-2018 - 21:24
Đã gửi 04-06-2018 - 21:24

Xí câu 5 ![]()
Các số có ước nguyên tố không vượt quá 7 có dạng $2^x.3^y.5^z.7^t$
x,y,z,t mỗi số có 2 TH chẵn, lẻ nên $2^x.3^y.5^z.7^t$ có 2.2.2.2=16 TH chẵn lẻ của bộ số (x;y;z;t)
Mà có 2 số nên theo nguyên lý Dirichlet tồn tại 2 số a,b có sao cho $a=2^{x_{1}}.3^{y_{1}}.5^{z_{1}}.7^{t_{1}}$ và $b=2^{x_{2}}.3^{y_{2}}.5^{z_{2}}.7^{t_{2}}$ và các số mũ ở các cơ số tương ứng cùng tính chẵn lẻ (ví dụ $x_{1};x_{2}$ cùng tính chẵn lẻ)
$\Rightarrow x_{1}+x_{2}=2n;y_{1}+y_{2}=2m;z_{1}+z_{2}=2p;t_{1}+t_{2}=2q$
$\Rightarrow a.b=2^{x_{1}+x_{2}}.3^{y_{1}+y_{2}}.5^{z_{1}+z_{2}}.7^{t_{1}+t_{2}}=2^{2n}.3^{2m}.5^{2p}.7^{2q}$
Bài viết đã được chỉnh sửa nội dung bởi Korkot: 04-06-2018 - 21:24
Nếu bạn cứ tiếp tục ca thán về cùng một nỗi buồn, cùng một việc nhỏ nhặt, bạn sẽ mãi mãi chìm đắm trong thất bại và sống một cuộc đời nhỏ bé. Hãy luôn nhớ rằng, ngay cả một ngày tồi tệ nhất cũng chỉ có 24 tiếng đồng hồ mà thôi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
#3
 Đã gửi 04-06-2018 - 21:54
Đã gửi 04-06-2018 - 21:54

Xí câu 5
Các số có ước nguyên tố không vượt quá 7 có dạng $2^x.3^y.5^z.7^t$
x,y,z,t mỗi số có 2 TH chẵn, lẻ nên $2^x.3^y.5^z.7^t$ có 2.2.2.2=16 TH chẵn lẻ của bộ số (x;y;z;t)
Mà có 2 số nên theo nguyên lý Dirichlet tồn tại 2 số a,b có sao cho $a=2^{x_{1}}.3^{y_{1}}.5^{z_{1}}.7^{t_{1}}$ và $b=2^{x_{2}}.3^{y_{2}}.5^{z_{2}}.7^{t_{2}}$ và các số mũ ở các cơ số tương ứng cùng tính chẵn lẻ (ví dụ $x_{1};x_{2}$ cùng tính chẵn lẻ)
$\Rightarrow x_{1}+x_{2}=2n;y_{1}+y_{2}=2m;z_{1}+z_{2}=2p;t_{1}+t_{2}=2q$
$\Rightarrow a.b=2^{x_{1}+x_{2}}.3^{y_{1}+y_{2}}.5^{z_{1}+z_{2}}.7^{t_{1}+t_{2}}=2^{2n}.3^{2m}.5^{2p}.7^{2q}$
Đề chắc cho số $20$ cho đẹp chứ $17$ là đủ rồi.
Mình gõ lời giải sắp xong mà bạn post rồi ![]() (
(
![]() $\sqrt{MF}$
$\sqrt{MF}$ ![]()
#4
 Đã gửi 04-06-2018 - 22:12
Đã gửi 04-06-2018 - 22:12

Làm luôn Câu 3:
a) Nếu x,y>3 thì có $x^2-2y^2 \equiv 1-2 \equiv -1 (mod 3) $ (vô lí do $x^2-2y^2=1$)
Vậy trong 2 số có 1 số =3
x=3 thì y=2 (nhận); y=3 thì x=19
$\Rightarrow$ kết luận
b) Đây là đề PTNK nhưng h mik phải đi ngủ nên mai mik làm cho
Bài viết đã được chỉnh sửa nội dung bởi Korkot: 05-06-2018 - 06:24
Nếu bạn cứ tiếp tục ca thán về cùng một nỗi buồn, cùng một việc nhỏ nhặt, bạn sẽ mãi mãi chìm đắm trong thất bại và sống một cuộc đời nhỏ bé. Hãy luôn nhớ rằng, ngay cả một ngày tồi tệ nhất cũng chỉ có 24 tiếng đồng hồ mà thôi.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
#5
 Đã gửi 04-06-2018 - 23:14
Đã gửi 04-06-2018 - 23:14

Gõ ra phòng mất đề
UBND TỈNH BẮC NINH ĐỀ THI TUYỂN SINH VÀO 10 THPT CHUYÊN
SỞ GD & ĐT NĂM HỌC 2018-2019
Môn thi: TOÁN( Dành cho thí sinh chuyên Toán và Tin)
Thời gian: 150 phút
Câu 1 (2,5 đ)
a) Rút gọn biểu thức
$$P= [\frac{a+\sqrt{a^2-b^2}}{a-\sqrt{a^2-b^2}} -\frac{a-\sqrt{a^2-b^2}}{a+\sqrt{a^2-b^2}}] :\frac{4\sqrt{a^4-a^2b^2}}{b^2}$$
với $|a|>|b|>0$
b) Cho phương trình $x^2+ax+b=0(1)$, x là ẩn , a, b là tham số. Tìm a,b sao cho (1) có nghiệm $x_{1};x_{2}$ thỏa mãn
$\left\{\begin{matrix} x_{1}-x_{2}=5 & & \\ x_{1}^{3}-x_{2}^{3}=35 & & \end{matrix}\right.$
Câu 2(2.5 đ)
a) Giải phương trình $\sqrt{x+3}+\sqrt{3x+1} =x+3$
b) Cho các số thực $a,b,c$ thảo mãn $0\leq a,b,c \leq 2$ và $a+b+c =3$ Tìm Max và Min của biểu thức
$$P=\frac{a^2+b^2+c^2}{ab+bc+ca}$$
Câu 3(1.5đ)
a)Tìm cặp số nguyên tố $(x;y)$ thỏa mãn $x^2-2y^2=1$
b) Chứng minh rằng nếu hiệu các lập phương của 2 số nguyên liên tiếp là bình phương của một số tự nhiên n thì n là tổng 2 số chính phương liên tiếp.
Câu 4( 3.0 đ)
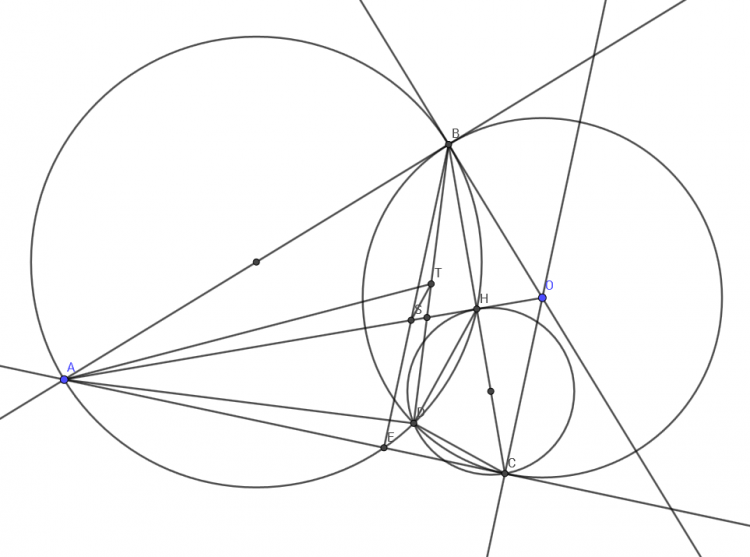
1)Từ A ngoài (O) vẽ 2 tiếp tuyến AB,AC (B,C là tiếp điểm ) . AO cắt BC tại H. Đường tròn đường kính CH cắt (O) tại điểm thứ 2 là D. Gọi T là trung điểm BD
a) Chứng minh ABHD nội tiếp
b) Gọi E là giao điểm thứ 2 của đường tròn đường kính AB với AC. S là giao của AO với BE. Chứng minh TS//HD
2) Cho $(O_{1})$ và $(O_{2})$ cắt nhau tại 2 điểm A,b. Gọi MN là tiếp tuyến chung của 2 đường tròn với M thuộc $(O_{1})$, N thuộc $O_{2}$ . Qua A kẻ đường thẳng d song song với MN cắt $O_{1}; O_{2}; BM;BN$ lần lượt tại C,D,F,G. Gọi E là giao của CM và DN. Chứng minh EF=EG
Câu 5
Cho 20 số tự nhiên, mỗi số có ước nguyên tố không vượt quá 7. Chứng minh rằng luôn chọn được ra 2 số sao cho tích của chúng là 1 số chính phương.
Bài viết đã được chỉnh sửa nội dung bởi MoMo123: 04-06-2018 - 23:15
- Tea Coffee, DOTOANNANG, NguyenHoaiTrung và 3 người khác yêu thích
#6
 Đã gửi 04-06-2018 - 23:35
Đã gửi 04-06-2018 - 23:35

Để mik làm giùm cho.
Min P=$\frac{a^{2}+b^{2}+c^{2}}{ab+bc+ca}\geq \frac{ab+bc+ca}{ab+bc+ca}\doteq 1$
Dấu "=" xảy ra <=> a=b=c=1
Max
Do $0\leq a,b,c\leq 2$ nên $(a-2)(b-2)(c-2)\leq 0< = > abc-2(ab+bc+ca)+4(a+b+c)-8\leq 0 <=>2(ab+bc+ca)\geq 4+abc\geq 4=>ab+bc+ca\geq 2$
$P=\frac{a^{2}+b^{2}+c^{2}}{ab+bc+ca}=\frac{9}{ab+bc+ca}-2\leq \frac{9}{2}-2=\frac{5}{2}$
Dấu "=" xảy ra <=> a=2, b=1, c=0 và các hoán vị
- MoMo123 và ThinhThinh123 thích
$\bigstar \bigstar \bigstar$ ALBERT EINSTEIN $\bigstar \bigstar \bigstar$
#7
 Đã gửi 05-06-2018 - 00:05
Đã gửi 05-06-2018 - 00:05

Câu 2a
Giải PT: $\sqrt{x+3}+\sqrt{3x+1}=x+3$ (điều kiện: $x\geq -\frac{1}{3}$)
Đặt: a = $\sqrt{x+3}$ ; b = $\sqrt{3x+1}$ $(a,b\geq 0)$
Ta có hệ phương trình:
$\left\{\begin{matrix} 3a^{2}-b^{2}=8\\ a+b=a^{2} \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} 3a^{2}-(a^{2}-a)^{2}-8=0\\ b=a^{2}-a \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} -a^{4}+2a^{3}+2a^{2}-8=0\\ b=a^{2}-a \end{matrix}\right.$
$\Leftrightarrow \left\{\begin{matrix} a^{3}(2-a)-2(2-a)(2+a)=0\\ b=a^{2}-a \end{matrix}\right.$
$\Leftrightarrow \left\{\begin{matrix} (2-a)(a^{3}-2a-4)=0\\ b=a^{2}-a \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} (2-a)(a-2)(a^{2}+2a+2)=0\\ b=a^{2}-a \end{matrix}\right.$
$\Leftrightarrow \left\{\begin{matrix} a=2\\ b=2 \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} \sqrt{x+3}=2\\ \sqrt{3x+1}=2 \end{matrix}\right.$$\Leftrightarrow \left\{\begin{matrix} x+3=4\\ 3x+1=4 \end{matrix}\right.$$\Leftrightarrow x=1$ (nhận)
Bài viết đã được chỉnh sửa nội dung bởi dchynh: 05-06-2018 - 01:07
#8
 Đã gửi 13-06-2018 - 13:39
Đã gửi 13-06-2018 - 13:39

2y^2=(x-1)(x+1) chia hết cho 4 nên y chia hết cho 2.....
#9
 Đã gửi 16-06-2018 - 16:20
Đã gửi 16-06-2018 - 16:20

bài hình:
1.
a.
$\widehat{BCD}=\widehat{ABD};\widehat{AHD}=\widehat{HCD}(\widehat{BCD})$
$\Rightarrow\widehat{ABD}=\widehat{AHD}$
$\Rightarrow$ ABHD nội tiếp (Q.E.D)
b.
$\widehat{DBH}=\widehat{DAH};\widehat{BDA}=\widehat{HDC}=90^{0}$
$\Rightarrow \Delta HAD=\Delta CBD$
$\Rightarrow \frac{AD}{AH}=\frac{BD}{BC}=\frac{2TD}{2HC}=\frac{TD}{HC}$
$\Rightarrow \Delta TAD=\Delta CAH$
$\Rightarrow \widehat{TAD}=\widehat{HAC}$
$\Rightarrow \widehat{TAS}=\widehat{DAF}=\widehat{DBF}(\widehat{TBS})$
$\Rightarrow$ BTSA nội tiếp$\Rightarrow \widehat{BAS}=\widehat{STG}=\widehat{BDH}$
$\Rightarrow$ST||HD (Q.E.D)
Bài viết đã được chỉnh sửa nội dung bởi Arthur Pendragon: 16-06-2018 - 16:58
"WHEN YOU HAVE ELIMINATED THE IMPOSSIBLE, WHATEVER REMAINS, HOWEVER IMPROBABLE, MUST BE THE TRUTH"
-SHERLOCK HOLMES-
#10
 Đã gửi 16-06-2018 - 16:56
Đã gửi 16-06-2018 - 16:56

bài hình (tiếp)
2.
MN||CD;$O_{1}M;O_{2}N\perp MN$
$\Rightarrow O_{1}M;O_{2}N$ lần lượt là đường trung trực của CA và DA
$\Rightarrow$ CH=HA; AI=IB;$\widehat{MHA}=\widehat{AIN}=90^{0}$
Mà HI||MN
$\Rightarrow$HINM là hình chữ nhật
$\Rightarrow HI=MN=\frac{1}{2}BC$
Suy ra MN là đường trung bình của $\Delta CED$ hay CM=ME
Lại có CH=HA nên MH là đường trung bình của $\Delta CAE$
$\Rightarrow$ MH||AE
Mà $MH \perp CA$
$\Rightarrow EA \perp BC$(1)
Mặt khác:
$MK^2=BK.KA;NK^2=BK.KA$
$\Rightarrow MK=NK$
$\Rightarrow GA=AF$(2)
Từ (1)và (2) ta suy ra AE là đường trung trực của GF
$\Rightarrow GE=EF$ (Q.E.D)
Bài viết đã được chỉnh sửa nội dung bởi Arthur Pendragon: 16-06-2018 - 17:04
"WHEN YOU HAVE ELIMINATED THE IMPOSSIBLE, WHATEVER REMAINS, HOWEVER IMPROBABLE, MUST BE THE TRUTH"
-SHERLOCK HOLMES-
#11
 Đã gửi 20-06-2018 - 16:15
Đã gửi 20-06-2018 - 16:15

Làm luôn Câu 3:
a) Nếu x,y>3 thì có $x^2-2y^2 \equiv 1-2 \equiv -1 (mod 3) $ (vô lí do $x^2-2y^2=1$)
Vậy trong 2 số có 1 số =3
x=3 thì y=2 (nhận); y=3 thì x=19
$\Rightarrow$ kết luận
b) Đây là đề PTNK nhưng h mik phải đi ngủ nên mai mik làm cho
Korkot, câu b, ý tưởng thế nào vậy , giúp mình nhé
. Mây tầng nào gặp gió tầng ấy. ![]()
#12
 Đã gửi 20-06-2018 - 16:45
Đã gửi 20-06-2018 - 16:45

Korkot, câu b, ý tưởng thế nào vậy , giúp mình nhé
Đây là ý tưởng
Giả sử $(a+1)^3-a^3=3a^2+3a+1=n^2$ thì biến đổi ra $3(2a+1)^2=(2n-1)(2n+1)$. Rồi chú ý $(2n-1,2n+1)=1$
Lập luận suy ra $2n-1=(2k+1)^2 $ (là số chính phương lẻ )
- 01634908884, Tea Coffee, nguyenthaibaolax1011 và 1 người khác yêu thích
Chỉ có hai điều là vô hạn: vũ trụ và sự ngu xuẩn của con người, và tôi không chắc lắm về điều đầu tiên.
Only two things are infinite, the universe and human stupidity, and I'm not sure about the former.
#13
 Đã gửi 20-07-2018 - 11:02
Đã gửi 20-07-2018 - 11:02

Van chua hieu tai sao 2n - 1 = (2k + 1)2Đây là ý tưởng
Giả sử $(a+1)^3-a^3=3a^2+3a+1=n^2$ thì biến đổi ra $3(2a+1)^2=(2n-1)(2n+1)$. Rồi chú ý $(2n-1,2n+1)=1$
Lập luận suy ra $2n-1=(2k+1)^2 $ (là số chính phương lẻ )
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh