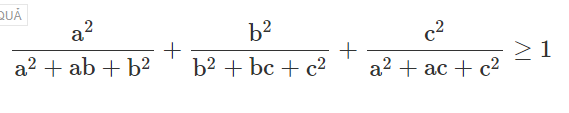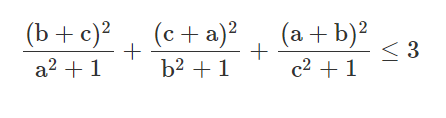a,b,c>0

$\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} \geq 1$
#1
 Đã gửi 19-12-2018 - 00:12
Đã gửi 19-12-2018 - 00:12

#2
 Đã gửi 19-12-2018 - 00:17
Đã gửi 19-12-2018 - 00:17

#3
 Đã gửi 19-12-2018 - 11:49
Đã gửi 19-12-2018 - 11:49

#4
 Đã gửi 19-12-2018 - 12:09
Đã gửi 19-12-2018 - 12:09

bài 1 : $\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} \geq \frac{(a+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
$\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} \geq \frac{(a+b)^2}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
$\frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)} \geq \frac{(b+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
Cộng 3 vế ta có :
$\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)}$ $\geq \frac{(a+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac} + \frac{(a+b)^2}{a^{2}+b^{2}+c^{2}+ab+bc+ac} + \frac{(b+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$ = 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)}$ $\geq$ 2 .
Mà : $\frac{c^{2}}{c(a+b+c)} + \frac{a^{2}}{a(a+b+c)} + \frac{b^2}{b(a+b+c)}$ = $\frac{c}{a+b+c}+\frac{b}{a+b+c}+\frac{a}{a+b+c}=\frac{a+b+c}{a+b+c}=1$
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{a^{2}}{a(a+b+c)} + \frac{b^2}{b(a+b+c)}$ $\geq$ 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} $ + 1 $\geq$ 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} $ $\geq$1
Cách này mình không nhớ nguồn ở đâu nhưng xin phép tác giả cho mình post lại cảm ơn ạ .
- Marshmello và Kitaro1006 thích
#5
 Đã gửi 19-12-2018 - 20:30
Đã gửi 19-12-2018 - 20:30

bài 1 : $\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} \geq \frac{(a+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
$\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} \geq \frac{(a+b)^2}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
$\frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)} \geq \frac{(b+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$
Cộng 3 vế ta có :
$\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)}$ $\geq \frac{(a+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac} + \frac{(a+b)^2}{a^{2}+b^{2}+c^{2}+ab+bc+ac} + \frac{(b+c)^{2}}{a^{2}+b^{2}+c^{2}+ab+bc+ac}$ = 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{a^{2}}{a(a+b+c)} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{b^2}{b(a+b+c)}$ $\geq$ 2 .
Mà : $\frac{c^{2}}{c(a+b+c)} + \frac{a^{2}}{a(a+b+c)} + \frac{b^2}{b(a+b+c)}$ = $\frac{c}{a+b+c}+\frac{b}{a+b+c}+\frac{a}{a+b+c}=\frac{a+b+c}{a+b+c}=1$
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} + \frac{c^{2}}{c(a+b+c)} + \frac{a^{2}}{a(a+b+c)} + \frac{b^2}{b(a+b+c)}$ $\geq$ 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} $ + 1 $\geq$ 2
<=> $\frac{a^{2}}{a^{2}+ab+b^{2}} +\frac{b^{2}}{b^{2}+bc+c^{2}} + \frac{c^{2}}{c^{2}+ac+a^{2}} $ $\geq$1
Cách này mình không nhớ nguồn ở đâu nhưng xin phép tác giả cho mình post lại cảm ơn ạ .
Cảm ơn bạn nhiều nha.
- vmf999 yêu thích
#6
 Đã gửi 19-12-2018 - 20:37
Đã gửi 19-12-2018 - 20:37

với $\it{b}= \text{mid}\left \{ \it{a},\,\it{b},\,\it{c} \right \},\,\it{Q}= \it{a}^{\,\it{3}}\it{b}+ \it{2}\,\it{a}^{\,\it{3}}\it{c}+ \it{2}\,\it{a}^{\,\it{2}}\it{b}^{\,\it{2}}+ \it{5}\,\it{a}^{\,\it{2}}\it{b}\it{c}+ \it{2}\,\it{c}^{\,\it{2}}\it{a}^{\,\it{2}}+ \it{2}\,\it{a}\it{b}^{\,\it{2}}\it{c}- \it{ab}\it{c}^{\,\it{2}}- \it{a}\it{c}^{\,\it{3}}- \it{b}^{\,\it{2}}\it{c}^{\,\it{2}}- \it{2}\,\it{b}\it{c}^{\,\it{3}}\geqq \it{0}$
Bài viết đã được chỉnh sửa nội dung bởi DOTOANNANG: 24-12-2018 - 09:18
- Kitaro1006 yêu thích
#7
 Đã gửi 20-12-2018 - 16:42
Đã gửi 20-12-2018 - 16:42

$$\sum\limits_{\it{cyc}} \frac{\it{a}^{\,\it{2}}}{\it{a}^{\,\it{2}}+ \it{ab}+ \it{b}^{\,\it{2}}}- \it{1}= \frac{\left ( \it{a}- \it{b} \right )^{\,\it{2}}}{\it{3}\left ( \it{a}^{\,\it{2}}+ \it{ab}+ \it{b}^{\,\it{2}} \right )}+ \frac{\left ( \it{b}- \it{c} \right )^{\,\it{2}}}{3\left ( \it{b}^{\,\it{2}}+ \it{bc}+ \it{c}^{\,\it{2}} \right )}+$$ $$+ \frac{\left ( \it{a}- \it{b} \right )\left ( \it{b}- \it{c} \right )\it{Q}}{\it{3}\left ( \it{a}^{\,\it{2}}+ \it{ab}+ \it{b}^{\,\it{2}} \right )\left ( \it{b}^{\,\it{2}}+ \it{bc}+ \it{c}^{\,\it{2}} \right )\left ( \it{c}^{\,\it{2}}+ \it{ca}+ \it{a}^{\,\it{2}} \right )}\geqq \it{0}$$
với $\it{b}= \text{mid}\left \{ \it{a},\,\it{b},\,\it{c} \right \},\,\it{Q}= \it{a}^{\,\it{3}}\it{b}+ \it{2}\,\it{a}^{\,\it{3}}\it{c}+ \it{2}\,\it{a}^{\,\it{2}}\it{b}^{\,\it{2}}+ \it{5}\,\it{a}^{\,\it{2}}\it{b}\it{c}+ \it{2}\,\it{c}^{\,\it{2}}\it{a}^{\,\it{2}}+ \it{2}\,\it{a}\it{b}^{\,\it{2}}\it{c}- \it{ab}\it{c}^{\,\it{2}}- \it{a}\it{c}^{\,\it{3}}- \it{b}^{\,\it{2}}\it{c}^{\,\it{2}}- \it{2}\,\it{b}\it{c}^{\,\it{3}}$SpoilerCái này lớp 8 chưa học mà bạn
- DOTOANNANG yêu thích
Đẹp trai nhưng không ai công nhận ![]()
#8
 Đã gửi 28-12-2018 - 23:52
Đã gửi 28-12-2018 - 23:52

$\frac{1+a}{1-a} + \frac{1+b}{1-b} + \frac{1+c}{1-c} \leq 2(\frac{a}{b}+\frac{b}{c} + \frac{c}{a} )$
#9
 Đã gửi 29-12-2018 - 00:01
Đã gửi 29-12-2018 - 00:01

$\frac{1+a}{1-a} + \frac{1+b}{1-b} +\frac{1+c}{1-c} \leq 2(\frac{a}{b}+\frac{b}{c}+\frac{c}{a})$
a,b,c dương . a+b+c=1
Bài viết đã được chỉnh sửa nội dung bởi Kitaro1006: 29-12-2018 - 00:02
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh