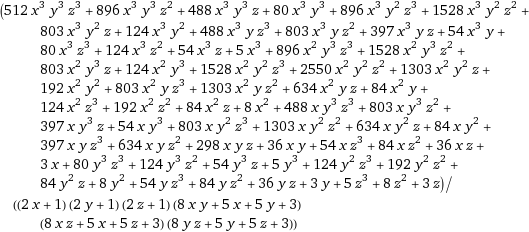Chủ đề này có 19 trả lời

[MyWorldMaths]

1. Cho a,b,c>0 và $ab^{2}c^{2}+a^{2}c+b=3c^{^{2}}$. Tìm max $P=\frac{c^{}4}{1+c^{4}(a^{}4+b^{4})}$

 

2. cho $0\leq a,b,c\leq 2$ và a+b+c=3 . cmr $a^{3}+b^{3}+c^{3}\leq 9$

 

3. Cho x,y,z>0 và $\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\sqrt{3}$. Tìm max $P=\sum \frac{\sqrt{2x^{2}+y^{2}}}{xy}$

 

4. Cho $0\leq a,b,c\leq 1$ . CMR $\sum \frac{a}{b+c+1}+(1-a)(1-b)(1-c)\leq 1$

 

5. Cho x,y,z >0. CMR $\sum \frac{\sqrt{y+z}}{x}\geq \frac{4(x+y+z)}{\sqrt{(y+z)(z+x)(x+y)}}$

 

6. Cho a,b,c>0 và$a^{2}+b^{2}+c^{2}=1$. CMR $\sum \frac{^{\sqrt{3a^{2}+4ab+3b^{2}}}}{ab}\geq 3\sqrt{30}$

[vmf999]

câu 1 đề thi chuyên tin lam sơn năm gần đây  

[vmf999]

câu 6 : $\sum \frac{\sqrt{3a^{2}+4ab+3b^{2}}}{ab}\geq \sum \frac{\sqrt{10ab}}{ab}=\sum \frac{\sqrt{10}}{\sqrt{ab}}\geq \sum \frac{9\sqrt{10}}{\sum \sqrt{ab}}\geq \frac{9\sqrt{10}}{a+b+c}\geq \frac{9\sqrt{10}}{\sqrt{3(\sum a^{2})}}=3\sqrt{30}$

[vmf999]

câu 5 : đpcm <=>$\prod \sqrt{x+y}(\sum \frac{\sqrt{y+z}}{x}) \geq 4(x+y+z)$

Ta có : $\prod \sqrt{x+y}(\sum \frac{\sqrt{y+z}}{x}) = \sum \frac{(y+z)\sqrt{(x+y)(x+z)}}{x}\geq \sum \frac{(y+z)(x+\sqrt{yz})}{x}=\sum (y+z)+\sum \frac{(y+z)\sqrt{yz}}{x}=2(x+y+z)+\sum \frac{(y+z)\sqrt{yz}}{x}\geq 2(x+y+z)+\sum \frac{2yz}{x}$

Để chứng minh hoàn tất ta chỉ ra : 

$\sum \frac{2yz}{x}\geq 2(x+y+z)$

Thật vậy : $\sum \frac{2yz}{x}\geq 2(x+y+z)$

<=>$\frac{2(\sum (yz)^{2})}{xyz}\geq 2(x+y+z)$

<=>$2(\sum (yz)^{2})\geq 2xyz(x+y+z) <=>\sum y^{2}z^{2}\geq xyz(x+y+z)$ (luôn đúng vì đây là bđt $a^{2}+b^{2}+c^{2}\geq ab+bc+ac$ trong đó a=xy,b=yz,c=xz)

 

[vmf999]

câu 3 đề là max hay min bạn với lại 3 hay $\sqrt{3}$

Bài viết đã được chỉnh sửa nội dung bởi vmf999: 21-12-2018 - 15:54

[vmf999]

câu 2 : gs a lớn nhất a thuộc khoảng [1,2] . (1$\leq$ a $\leq$ 2 ) 

Ta có : $b^{3} + c^{3} \leq (b+c)^{3}$ = $(3-a)^{3}$

Ta có : $a^{3} + b^{3} + c^{3} \leq$ $a^{3} + (3-a)^3$ = 27-27a+$9a^{2} -a^{3} + a^{3}$=27-27a+$9a^{2}$

Ta chứng minh : 27-27a+$9a^{2}$ $\leq$ 9 

<=>$9a^{2} - 27a +18 \leq$ 0 

<=> 9($a^{2}$ -3a+2) $\leq$ 0 

<=> 9(a-1)(a-2) $\leq$ 0 (luôn đúng với mọi a thuộc khoảng [1,2]

dấu bằng xảy ra khi (a,b,c)=(0,1,2) và các hoán vị 

[DOTOANNANG]

Với $\it{x},\,\it{y},\,\it{z}\geqq \it{0}$ thì: $\it{0}< \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}\leqq 1$

Xét trường hợp ít nhất một trong ba biến bằng $0$ , không mất tính tổng quát trong chứng minh, chẳng hạn $\it{a}$ , khi đó:

 

$$\it{1}- \sum\limits_{cyc}\,\frac{\it{a}}{\it{b}+ \it{c}+ \it{1}}- \left ( \it{1}- \it{a} \right )\left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )= \frac{\it{bc}\left ( \it{1}- \it{bc} \right )}{\left ( \it{b}+ \it{1} \right )\left ( \it{c}+ \it{1} \right )}\geqq \it{0}$$

 

Giờ đây, ta chỉ cần đặt: $\it{a}= \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\it{b}= \frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\it{c}= \frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}$ , sẽ có được biểu thức vế trái với hệ số của $\it{x},\,\it{y},\,\it{z}$ đều không âm!

Spoiler

 

[MyWorldMaths]

câu 1 đề thi chuyên tin lam sơn năm gần đây

[MyWorldMaths]

Cậu chữa hộ mình đc ko? Nói ý chính thôi. Thanks

[MyWorldMaths]

câu 3 đề là max hay min bạn với lại 3 hay $\sqrt{3}$

[MyWorldMaths]

Cho mình xin lỗi ấy là tìm MIN còn kia là căn 3 nhá
Cậu làm với 3 thì như thế nào

[MyWorldMaths]

câu 1 đề thi chuyên tin lam sơn năm gần đây  

cậu trả lời luôn hộ mình đc ko ? nói ý chính thôi. ko cậu gửi link của đề thi ấy cho mình mượn. Cám ơn nhiều!!!

[vmf999]

cậu trả lời luôn hộ mình đc ko ? nói ý chính thôi. ko cậu gửi link của đề thi ấy cho mình mượn. Cám ơn nhiều!!

Bạn cần gấp không @@ giờ mình bận quá trưa mai mình gửi cho bạn @@ 

[MyWorldMaths]

Bạn cần gấp không @@ giờ mình bận quá trưa mai mình gửi cho bạn @@ 

Thanks bạn

[vmf999]

câu 1 : @@ 

$ab^{2}c^{2} + a^{2}c + b = 3c^{2}$

<=> $ab^{2} + a^2/c + b/c^2 =3$

đặt a=x , b=y , $\frac{1}{c}$=z

 

=>$xy^{2} + x^{2}z + yz^{2} =3$

Ta có : $\frac{c^{4}}{1+c^{4}(a^{4}+b^{4})}$ 

= $\frac{1}{\frac{1}{c^{4}} + a^{4} + b^{4}}$ 

= $\frac{1}{x^{4}+y^{4}+z^{4}}$

Ta có : 

$x^{4} + y^{4} + y^{4} + 1 \geq 4xy^{2}$ (1)

$x^{4} + x^{4} + z^{4} + 1 \geq 4x^{2}z$ (2)

$z^{4} + z^{4} +y^{4} + 1 \geq 4z^{2}y$ (3)

(1),(2),(3) suy ra : 

$x^{4} + y^{4} + y^{4} + 1 +x^{4} + x^{4} + z^{4} + 1 + z^{4} + z^{4} +y^{4} + 1  \geq 4xy^{2} +4x^{2}z +4z^{2}y$

<=> 3($x^{4} + y^{4} + z^{4} ) + 3 \geq 4xy^{2} +4x^{2}z +4z^{2}y$

<=> 3($x^{4} + y^{4} + z^{4} ) +3 \geq 12$

<=>$x^{4} + y^{4} + z^{4} \geq 3$

=> $\frac{1}{x^{4}+y^{4}+z^{4}}$ $\leq$ $\frac{1}{3}$

Dấu = khi a=b=c=1

[vmf999]

câu 3 bạn còn cần không để hôm nào mình gửi luôn cho 

[DOTOANNANG]

$\lceil\,\,2\,\,\rfloor$ Tổng quát:

$\it{a},\,\it{b},\,\it{c}\in \left [ \it{0},\,\it{2} \right ],\,\,\it{a}+ \it{b}+ \it{c}= \it{3}$ thì: $\it{a}^{\,\it{p}}+ \it{b}^{\,\it{p}}+ \it{c}^{\,\it{p}}\leqq \it{2}^{\,\it{p}}+ \it{1}\,\,\left ( \it{p}\geqq \it{1} \right )$

 

[MyWorldMaths]

Với $\it{x},\,\it{y},\,\it{z}\geqq \it{0}$ thì: $\it{0}< \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}\leqq 1$

Xét trường hợp ít nhất một trong ba biến bằng $0$ , không mất tính tổng quát trong chứng minh, chẳng hạn $\it{a}$ , khi đó:

 

$$\it{1}- \sum\limits_{cyc}\,\frac{\it{a}}{\it{b}+ \it{c}+ \it{1}}- \left ( \it{1}- \it{a} \right )\left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )= \frac{\it{bc}\left ( \it{1}- \it{bc} \right )}{\left ( \it{b}+ \it{1} \right )\left ( \it{c}+ \it{1} \right )}\geqq \it{0}$$

 

Giờ đây, ta chỉ cần đặt: $\it{a}= \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\it{b}= \frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\it{c}= \frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}$ , sẽ có được biểu thức vế trái với hệ số của $\it{x},\,\it{y},\,\it{z}$ đều không âm!

Spoiler

MSP17315137b4beb9c52f364000042fi2126dh5h0g62.gif

Bạn có thể trả lời cụ thể hơn ko. Mình ko hiểu! cám ơn

[MyWorldMaths]

câu 3 bạn còn cần không để hôm nào mình gửi luôn cho 

Được. cám ơn bạn. 

Mình có mới đăng một số bài. bạn vào nghiên cứu thử nhé!!

[DOTOANNANG]

Với $\it{x},\,\it{y},\,\it{z}\geqq \it{0}$ thì: $\it{0}< \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}\leqq 1$

Xét trường hợp ít nhất một trong ba biến bằng $0$ , không mất tính tổng quát trong chứng minh, chẳng hạn $\it{a}$ , khi đó:

 

$$\it{1}- \sum\limits_{cyc}\,\frac{\it{a}}{\it{b}+ \it{c}+ \it{1}}- \left ( \it{1}- \it{a} \right )\left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )= \frac{\it{bc}\left ( \it{1}- \it{bc} \right )}{\left ( \it{b}+ \it{1} \right )\left ( \it{c}+ \it{1} \right )}\geqq \it{0}$$

 

Giờ đây, ta chỉ cần đặt: $\it{a}= \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\it{b}= \frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\it{c}= \frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}$ , sẽ có được biểu thức vế trái với hệ số của $\it{x},\,\it{y},\,\it{z}$ đều không âm!

Spoiler

Cho $\it{x}\in \left ( \it{0},\,\it{1} \right ]\Rightarrow \frac{\it{1}- \it{x}}{\it{x}}\geqq \it{0}$ . Sử dụng $\lceil$ Phép thế Ravi $\rfloor$ , ta đặt: $\it{u}= \frac{\it{1}- \it{x}}{\it{x}}\rightarrow \it{x}= \frac{\it{1}}{\it{1}+ \it{u}}\,\,\left ( \it{u}\geqq \it{0} \right )$ .

Áp dụng cho bài trên tương tự, chỉ cần xét $\it{a}+ \it{b}+ \it{c}> 0$ . Bất đẳng thức đã cho tương đương với:

$$\sum\limits_{cyc}\,\left ( \frac{\it{a}}{\it{a}+ \it{b}+ \it{c}}- \frac{\it{a}}{\it{b}+ \it{c}+ \it{1}} \right )\geqq \left ( \it{1}- \it{a} \right )\left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )$$

$$\Leftrightarrow \sum\limits_{cyc}\frac{\it{a}\left ( \it{1}- \it{a} \right )}{\it{b}+ \it{c}+ \it{1}}\geqq \left ( \it{1}- \it{a} \right )\left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )\left ( \it{a}+ \it{b}+ \it{c} \right )$$

$$\Leftrightarrow \sum\limits_{cyc}\left [ \it{a}\left ( \it{1}- \it{a} \right )\left ( \frac{\it{1}}{\it{1}+ \it{b}+ \it{c}}- \left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right ) \right ) \right ]\geqq \it{0}\Leftarrow \frac{\it{1}}{\it{1}+ \it{b}+ \it{c}}- \left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )\geqq \it{0}$$

Đó là điều ta cần chứng minh với: $\it{b}= \frac{\it{1}}{\it{1}+ \it{m}},\,\it{c}= \frac{\it{1}}{\it{1}+ \it{n}}\Rightarrow$ $\frac{\it{1}}{\it{1}+ \it{b}+ \it{c}}\geqq \left ( \it{1}- \it{b} \right )\left ( \it{1}- \it{c} \right )\Leftrightarrow \frac{\left ( \it{1}+ \it{m} \right )\left ( \it{1}+ \it{n} \right )}{\left ( \it{1}+ \it{m} \right )\left ( \it{1}+ \it{n} \right )+ \it{m}+ \it{n}+ \it{2}}\geqq \frac{\it{mn}}{\left ( \it{1}+ \it{m} \right )\left ( \it{1}+ \it{n} \right )}\Leftrightarrow \left ( \it{m}+ \it{n}+ \it{1} \right )^{\,\it{2}}\geqq \it{mn}$

Ngoài ra, lí giải cho cách đặt ẩn trên:

$$\it{a}= \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}},\,\it{b}= \frac{\it{1}+ \it{y}}{\it{1}+ \it{y}+ \it{y}},\,\it{c}= \frac{\it{1}+ \it{z}}{\it{1}+ \it{z}+ \it{z}}$$

Với mọi phân số $\frac{\it{u}}{\it{v}}\in \left ( \it{0},\,\it{1} \right ]\Leftrightarrow \frac{\it{u}+ \it{k}}{\it{v}+ \it{k}} \in \left ( \it{0},\,\it{1} \right ]\,\,\left ( \it{k}\geqq 0 \right )$ , hay với bất kì $\frac{\text{U}}{\text{V}}= \frac{\it{1}}{\it{1}+ \it{x}}\Rightarrow \frac{\it{u}}{\it{v}}= \frac{\it{1}+ \it{x}}{\it{1}+ \it{x}+ \it{x}}$ .

Spoiler

$\lceil$ https://diendantoanh...e-1#entry712425 $\rfloor$

Ngoài ra với bất kì $\it{a}= \frac{\it{1}+ \it{kx}}{\it{1}+ \left ( \it{k}+ \it{1} \right )\it{x}},\,\it{b}= \frac{\it{1}+ \it{ky}}{\it{1}+ \left ( \it{k}+ \it{1} \right )\it{y}},\,\it{c}= \frac{\it{1}+ \it{kz}}{\it{1}+ \left ( \it{k}+ \it{1} \right )\it{z}}\,\,\left ( k\geqq \it{0} \right )$ , sẽ có được biểu thức vế trái với hệ số của $\it{x},\,\it{y},\,\it{z}$  đều không âm!