Chủ đề này có 20 trả lời

[tritanngo99]

Phần I: TỌA ĐỘ VUÔNG GÓC VÀ TỌA ĐỘ CỰC.

1) Tọa độ trên đường thẳng. Chia đoạn thẳng theo một tỷ số cho trước.

Điểm $M$ của trục tọa độ $Ox$ có hoành độ $x$ được ký hiệu là $M(x)$.

Khoảng cách $d$ giữa các điểm $M_1(x_1)$ và $M_2(x_2)$ phân bố tùy ý trên trục được xác định bởi công thức $d=|x_2-x_1|(1)$.

Giả sử cho đoạn $[AB]$ trên một đường thẳng bất kỳ ($A$ là đầu, $B$ là cuối của nó), khi đó mọi điểm thứ ba $C$ của đường thẳng này chia đoạn $[AB]$ theo một tỷ số $\lambda$ nào đấy, trong đó $\lambda=\pm \frac{|AC|}{|CB|}$.

Nếu các đoạn thẳng $[AC]$ và $[CB]$ cùng hướng về một phía, thì $\lambda$ nhận dấu $<<+>>$, còn nếu đoạn $[AC]$ và $[CB]$ hướng về hai phía khác nhau thì $\lambda$ nhận dấu $<<->>$. Nói một cách khác, $\lambda$ nhận dấu dương nếu điểm $C$ nằm giữa $A$ và $B$ và âm nếu điểm $C$ nằm trên đường thẳng nhưng ở ngoài đoạn $[AB]$.

 Nếu các điểm $A$ và $B$ nằm trên trục $Ox$ thì tọa độ $x$ của điểm $C(x)$, điểm chia theo tỷ số $\lambda$ đoạn thẳng giữa các điểm $A(x_1)$ và $B(x_2)$ được xác định theo công thức: $x=\frac{x_1+\lambda x_2}{1+\lambda}$. 

Đặc biệt khi $\lambda=1$ ta được công thức cho tọa độ điểm giữa của đoạn thẳng $AB: x=\frac{x_1+x_2}{2}(2)$.

Các ví dụ:

1. Vẽ trên đường thẳng các điểm $A(3),B(-2),C(0),D(\sqrt{2}),E(-3\frac{1}{2})(3)$.

2. Dùng bốn điểm chia đoạn thẳng $[AB]$ thành $5$ phần bằng nhau. Xác định tọa độ của điểm chia gần $A$ nhất, nếu $A(-3),B(7)$.

Giải: Giả sử $C(x)$ là điểm cần tìm, khi đó $\lambda=\frac{|AC|}{|CB|}=\frac{1}{4}$.

Theo công thức $(2)$ ta có: $x=\frac{x_1+\lambda x_2}{1+\lambda}=\frac{-3+\frac{1}{4}.7}{1+\frac{1}{4}}=-1$, nghĩa là $C(-1)$.

3. Cho các đầu mút của đoạn $[AB]:A(1),B(5)$; điểm $C$ nằm ngoài đoạn $AB$ và khoảng cách từ nó đến $A$ gấp ba lần khoảng cách đến $B$. Xác định tọa độ của điểm $C$.

Giải: Dễ thấy rằng: $\lambda=-\frac{|AC|}{|BC|}=-3$.Vì vậy: $x=\frac{1-3.5}{1-3}=7$, nghĩa là $C(7)$.

4. Xác định khoảng cách giữa các điểm: 1) $M(3)$ và $N(-5)$; 2) $P(\frac{-11}{2})$ và $Q=\frac{-5}{2}$.

5. Tìm các tọa độ điểm giữa các đoạn, nếu biết hai đầu mút của nó: 1) $A(-6)$ và $B(7)$; 2) $C(-5)$ và $D(1/2)$.

6. Tìm điểm $M$ đối xứng với điểm $N(-3)$ qua điểm $P(2)$.

7. Dùng hai điểm chia đoạn $[AB]$ thành ba phần bằng nhau. Xác định tọa độ các điểm nếu $A(-1),B(5)$.

8. Cho các điểm $A(-7),B(-3)$. Các điểm $C$ và $D$ nằm ngoài đoạn $[AB]$ và $|CA|=|BD|=\frac{|AB|}{2}$. Xác định tọa độ các điểm $C$ và $D$.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 01-02-2019 - 07:00

[tritanngo99]

2) Tọa độ vuông góc trên mặt phẳng. Các bài toán đơn giản nhất.

   Nếu cho hệ tọa độ đềcác vuông góc $Oxy$ trên mặt phẳng thì điểm $M$ có các tọa độ $x$ và $y$ trên mặt phẳng này, được ký hiệu là $M(x,y)$.

   Khoảng cách $d$ giữa các điểm $M_1(x_1;y_1)$ và $M_2(x_2;y_2)$ được xác định theo công thức $d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}(1)$.

   Đặc biệt khoảng cách $d$ từ điểm $M(x;y)$ đến gốc tọa độ được xác định theo công thức $d=\sqrt{x^2+y^2}(2)$.

Các tọa độ của điểm $C(x;y)$- điểm chia theo tỷ số $\lambda$ đoạn thẳng giữa các điểm $A(x_1;y_1)$ và $B(x_2;y_2)$ được xác định theo công thức $x=\frac{x_1+\lambda x_2}{1+\lambda};y=\frac{y_1+\lambda y_2}{1+\lambda}(3)$.

Đặc biệt khi $\lambda=1$ ta có công thức cho các tọa độ điểm giữa của đoạn $[AB]$: $x=\frac{x_1+x_2}{2};y=\frac{y_1+y_2}{2}(4)$.

Diện tích tam giác có các đỉnh $A(x_1;y_1),B(x_2;y_2),C(x_3;y_3)$ được tính theo công thức:

$S=\frac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|=\frac{1}{2}|(x_2-x_1)(y_3-y_1)-(x_3-x_1)(y_2-y_1)|(5)$.

Công thức tính diện tích tam giác có thể viết dưới dạng $S=\frac{1}{2}|\Delta|(6)$,

trong đó: $\Delta=\begin{align*}\begin{vmatrix} 1&1&1\\ x_1&x_2&x_3\\ y_1&y_2&y_3 \end{vmatrix}\end{align*}$ 

Các ví dụ: 

9. Vẽ trên mặt phẳng tọa độ các điểm $A(4;3),B(-2;5),C(5;-2),D(-4;-3),E(-6;0),F(0;4)$.

10. Tìm khoảng cách giữa các điểm $A(3;8)$ và $B(-5;14)$.

Giải: Áp dụng công thức $(1)$ ta được: $d=\sqrt{(-5-3)^2+(14-8)^2}=\sqrt{64+36}=10$.

11. Chứng minh rằng tam giác $ABC$ với các đỉnh $A(-3;-3), B(-1;3),C(11;-1)$ là tam giác vuông.

Giải: Ta tìm độ dài các cạnh của tam giác: $|AB|=\sqrt{(-1+3)^2+(3+3)^2}=\sqrt{40},|BC|=\sqrt{(11+1)^2+(-1-3)^2}=\sqrt{160},|AC|=\sqrt{(11+3)^2+(-1+3)^2}=\sqrt{200}$.

Vì $|AB|^2=40,|BC|^2=160,|AC|^2=200$ nên $|AB|^2+|BC|^2=|AC|^2$. Do đó tổng các bình phương độ dài hai cạnh của tam giác bằng bình phương độ dài cạnh thứ ba. Từ đó ta kết luận $ABC$ là tam giác vuông và $AC$ là cạnh huyền của nó.

12. Cho các mút của đoạn $[AB]:A(-2;5),B(4;17)$. Điểm $C$ nằm trên đoạn $[AB]$, có khoảng cách đến $A$ gấp đôi khoảng cách đến $B$. Xác định các tọa độ của điểm $C$.

Giải: Vì $|AC|=2|CB|$ nên $\lambda=\frac{|AC|}{|CB|}=2$. Ở đây $x_1=-2,y_1=5,x_2=4,y_2=17$. Do đó: $\overline{x}=\frac{-2+2.4}{1+2},\overline{y}=\frac{5+2.17}{1+2}=13$, nghĩa là: $C(2;13)$.

13. Điểm giữa của đoạn thẳng $[AB]$ là điểm $C(2;3)$. Xác định tọa độ của điểm $A$, nếu $B(7;5)$.

Giải: Ở đây $\overline{x}=2,\overline{y}=3,x_2=7,y_2=5$ suy ra $2=\frac{x_1+7}{2},3=\frac{y_1+5}{2}$. Do đó: $x_1=-3,y_1=1$ nghĩa là $A(-3;1)$.

14. Cho các đỉnh của tam giác $ABC:A(x_1;y_1),B(x_2;y_2),C(x_3;y_3)$. Xác định tọa độ giao điểm các đường trung tuyến của tam giác.

Giải: Ta tìm các tọa độ của điểm giữa $D$ của đoạn $[AB]: x_D=\frac{x_1+x_2}{2};y_D=\frac{y_1+y_2}{2}$.

 Giao điểm $M$ của các đường trung tuyến chia đoạn $[CD]$ theo tỷ số $2:1$ tính từ điểm $C$. Do đó các tọa độ của điểm $M$ được tính theo các công thức: $\overline{x}=\frac{x_3+2x_D}{1+2},\overline{y}=\frac{y_3+2y_D}{1+2}$,

nghĩa là: $\overline{x}=\frac{x_3+2.\frac{x_1+x_2}{2}}{3},\overline{y}=\frac{y_3+\frac{y_1+y_2}{2}}{3}$.

Cuối cùng: $\overline{x}=\frac{x_1+x_2+x_3}{3},\overline{y}=\frac{y_1+y_2+y_3}{3}$.

15. Tìm diện tích tam giác có các đỉnh $A(-2;-4),B(2;8)$ và $C(10;2)$.

Giải: Áp dụng công thức $(5)$ ta được: $S=\frac{1}{2}|(2+2)(2+4)-(10+2)(8+4)|=\frac{1}{2}|24-144|=60$.

16. Tìm khoảng cách giữa các điểm:

a) $A(2;3)$ và $B(-10;-2)$

b) $C(\sqrt{2};-\sqrt{7})$ và $D(2\sqrt{2};0)$.

17. Chứng minh rằng tam giác có các đỉnh $A(4;3),B(7;6)$ và $C(2;11)$ là tam giác vuông.

18. Chứng minh rằng tam giác có các đỉnh $A(2;-1),B(4;2),C(5;1)$ là tam giác cân.

19. Cho các đỉnh của tam giác $A(-1;-1),B(0,-6)$ và $C(-10;-2)$. Tìm độ dài của đường trung tuyến vẽ từ đỉnh $A$.

20. Cho các mút của đoạn $[AB]:A(-3;7)$ và $B(5;11)$. Dùng ba điểm để chia đoạn thẳng thành bốn phần bằng nhau. Xác định tọa độ của các điểm đã chia.

21. Tìm diện tích tam giác có các đỉnh $A(1;5),B(2;7)$ và $C(4;11)$.

22. Cho ba đỉnh liên tiếp của hình bình hành: $A(11;4),B(-1;-1),C(5;7)$. Xác định tọa độ của đỉnh thứ tư.

23. Cho hai đỉnh $A(3;8)$ và $B(10;2)$ của tam giác và giao điểm $M(1;1)$ của các đường trung tuyến. Tìm các tọa độ của đỉnh thứ ba của tam giác đó.

24. Cho các đỉnh của tam giác: $A(7;2),B(1;9)$ và $C(-8;-11)$. Tìm khoảng cách từ giao điểm của các đường trung tuyến đến các đỉnh của tam giác.

25. Các điểm $L(0;0),M(3;0)$ và $N(0;4)$ là điểm giữa các cạnh của một tam giác. Tính diện tích tam giác đó.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 01-02-2019 - 07:00

[tritanngo99]

3) Tọa độ cực.

Trong hệ tọa độ cực vị trí của điểm $M$ trên mặt phẳng được xác định bằng khoảng cách $|OM|=\rho$ từ $M$ đến cực $O$($\rho$ là bán kính cực của điểm) và góc $\theta$ tạo thành bởi đoạn $[OM]$ với trục $Ox$(\theta là góc cực của điểm). Góc $\theta$ được xem là dương khi tính từ trục cực ngược chiều kim đồng hồ.

  Nếu điểm $M$ có các tọa độ cực $\rho>0$ và $\theta>0$, trong đó $0\le \theta<2\pi$, thí ứng với nó còn cả một tập hợp vô số các cặp tọa độ cực $(\rho;\theta+2k\pi)$ và $(-\rho;\theta+(2k+1)\pi)$, trong đó $k\in \mathbb{Z}$. 

  Nếu gốc của hệ tọa độ Đềcác vuông góc trùng với cực, còn trục $Ox$ hướng theo trục cực thì các tọa độ vuông góc $x$ và $y$ của điểm $M$ và các tọa độ cực $\rho$ và $\theta$ của nó sẽ liên hệ với nhau bằng các công thức sau đây: 

$x=\rho cos\theta,y=\rho sin\theta\text{    }(1)$

$\rho=\sqrt{x^2+y^2},tan\theta=\frac{y}{x}\text{    }(2)$.

Các ví dụ:

26. Vẽ các điểm được cho bằng các tọa độ cực: $A(4;\frac{\pi}{4}),B(2;\frac{4}{3}\pi),C(3;\frac{-\pi}{6}),D(-3;\frac{\pi}{3}),E(0;\alpha),F(-1;\frac{-3}{4}\pi)$.

27. Tìm các tọa độ cực của điểm $M(1;-\sqrt{3})$, nếu cực trùng với gốc tọa độ còn trục cực có hướng dương của trục hoành.

Giải. Theo đẳng thức $(2)$ ta có: $\rho=\sqrt{1^2+(-\sqrt{3})^2}=2,tan\theta=-\sqrt{3}$.

Hiển nhiên, điểm $M$ nằm trong góc phần tư thứ tư nên $\theta=\frac{5\pi}{3}$.

Vậy $M(2;\frac{5}{3}\pi)$.

28. Tìm các tọa độ vuông góc của điểm $A(2\sqrt{2};\frac{3\pi}{4})$, nếu cực trùng với gốc tọa độ còn trục cực hướng theo trục hoành.

Giải. Dùng công thức $(1)$ ta có: $x=2\sqrt{2}cos\frac{3\pi}{4}=-2;y=2\sqrt{2}sin\frac{3\pi}{4}=2$. Vậy $A(-2;2)$.

29. Tìm tọa độ cực của các điểm: $A(2\sqrt{3};2),B(0;-3),C(-4;4),D(\sqrt{2};-\sqrt{2}),E(-\sqrt{2};-\sqrt{6}),F(-7;0)$.

30. Tìm tọa độ vuông góc của các điểm $A(10;\frac{\pi}{2}),B(2;\frac{5}{4}\pi),C(0;\frac{\pi}{10}),D(1;\frac{-\pi}{4}),E(-1;\frac{\pi}{4}),F(-1;\frac{-\pi}{4})$.

31. Tìm khoảng cách giữa các điểm $M_1(\rho_1;\theta_1)$ và $M_2(\rho_2;\theta_2)$.

Hướng dẫn: Áp dụng định lý côsin vào tam giác $OM_1M_2$.

32. Tìm khoảng cách giữa các điểm $M(3;\frac{\pi}{4})$ và $N(4;\frac{3}{4}\pi)$.

33. Tìm các tọa độ cực đối xứng với điểm $M(\rho;\theta)$ qua trục cực.

34. Tìm các tọa độ cực của điểm đối xứng với điểm $M(\rho;\theta)$ qua cực.

35. Tìm tọa độ cực của các điểm đối xứng với các điểm $(3;\frac{\pi}{6}),(5;\frac{2\pi}{3})$ và $(2;\frac{-\pi}{6})$:

a) Qua cực

b) Qua trục cực.

36. Tìm các tọa độ cực của điểm đối xứng với điểm $M(\rho;\theta)$ đối với đường thẳng đi qua cực và thẳng góc với trục cực.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 01-02-2019 - 07:00

[tritanngo99]

4) Phương trình của đường.

 Mỗi đường trên mặt phẳng $xOy$ được xem như một tập hợp các điểm tương ứng với một phương trình nào đấy liên hệ các tọa độ của điểm $M(x;y)$ tùy ý nằm trên đường đó (" điểm chạy "). Phương trình như thế được gọi là phương trình của đường đã cho.

 Khi thay các tọa độ của điểm bất kỳ nằm trên đường đã cho vào phương trình, phương trình này trở thành đồng nhất thức. Còn khi thay các tọa độ của điểm bất kỳ không nằm trên đường vào phương trình của đường thì phương trình không được thỏa mãn.

Các ví dụ:

37. Một trong các đầu mút của đoạn thẳng có độ dài bằng $c$ di chuyển theo trục hoành, còn đầu mút kia của đoạn thẳng di chuyển theo trục tung. Tìm phương trình của đường do điểm giữa của đoạn thẳng này vạch ra.

Giải. Giả sử $M(x,y)$ là điểm giữa của đoạn thẳng. Độ dài của đoạn $[OM]$( độ dài của trung tuyến) bằng nửa cạnh huyền, nghĩa là $|OM|=\frac{c}{2}$. Mặt khác $|OM|=\sqrt{x^2+y^2}$( khoảng cách từ điểm $M$ đến gốc tọa độ).

Vì vậy ta dẫn đến phương trình $\sqrt{x^2+y^2}=\frac{c}{2}$ hay $x^2+y^2=\frac{c^2}{4}$. Đó chính là phương trình cần tìm.

Về mặt hình học, rõ ràng đường cần tìm là đường tròn bán kính $\frac{c}{2}$ với tâm tại gốc tọa độ.

38. Lập phương trình của đường, mà khoảng cách từ mỗi điểm của nó đến điểm $F(0;\frac{1}{4})$ bằng khoảng cách cũng từ điểm ấy đến đường đường thẳng $y=\frac{-1}{4}$.

Giải. Trên đường cần tìm ta lấy điểm $M(x;y)$ tùy ý. Khoảng cách từ điểm $M$ đến điểm $F$ được xác định theo công thức tính khoảng cách giữa hai điểm: $|MF|=\sqrt{(x-0)^2+(y-\frac{1}{4})^2}$.

Khoảng cách từ điểm $M$ đến đường thẳng $y=\frac{-1}{4}$ tìm được từ hình ảnh hình học đơn giản (h.1): 

$|MN|=|MK|+|KN|=y+\frac{1}{4}$.

Hình 1.

Vì theo điều kiện của đề bài, đẳng thức $|MF|=|MN|$ thỏa mãn với điểm $M$ bất kỳ nằm trên đường cần tìm, nên phương trình của đường có thể viết dưới dạng: $\sqrt{x^2+(y-\frac{1}{4})^2}=y+\frac{1}{4}$;

hay $x^2+y^2-\frac{1}{2}y+\frac{1}{16}=y^2+\frac{1}{2}y+\frac{1}{16}$ nghĩa là $y=x^2$.

Đường có phương trình $y=x^2$ được gọi là đường parabôn.

39. Lập phương trình quỹ tích các điểm mà tích khoảng cách từ chúng đến các điểm $F_1(a;0)$ và $F_2(-a;0)$ là một đại lượng không đổi và bằng $a^2$.

Giải. Trên đường cần tìm ta lấy điểm $M(x;y)$ tùy ý. Khoảng cách từ điểm đó đến các điểm $F_1(a;0)$ và $F_2(-a;0)$ là $r_1=\sqrt{(x-a)^2+b^2},r_2=\sqrt{(x+a)^2+y^2}$. Từ điều kiện của bài toán suy ra $r_1.r_2=a^2$ .

Do đó đường cần tìm có phương trình $\sqrt{(x-a)^2+y^2}.\sqrt{(x+a)^2+y^2}=a^2$.

Ta đưa phương trình này về dạng hữu tỷ: $(x^2+a^2+y^2-2ax)(x^2+a^2+y^2+2ax)=a^4$,

từ đó: $(x^2+a^2+y^2)^2-4a^2x^2=a^4$,

hay, cuối cùng $(x^2+y^2)^2=2a^2(x^2-y^2)$

Đường cong vừa tìm thấy được gọi là đường lemniscat.

40. Lập phương trình đường lemniscat trong tọa độ cực và vẽ đường cong đó.

Giải. Đưa phương trình $(x^2+y^2)^2=2a^2(x^2-y^2)$ về tọa độ cực theo các công thức: $x=\rho cos\theta,y=\rho sin\theta$ ta được phương trình đường lemniscat trong tọa độ cực $\rho^2=2a^2.cos\theta$. 

Ta vẽ đường cong đó.

Giải phương trình đối với $\rho:\rho=\pm a\sqrt{2cos 2\theta}$. Từ nhận xét rằng vế phải của đẳng thức có hai dấu $\pm$ và phương trình không đổi khi thay $\theta$ bằng $-\theta$, ta kết luận đường lemniscat đối xứng qua các trục $Ox$ và $Oy$. Ta nghiên cứu dạng của lemniscat trong góc phần tư thứ nhất, nghĩa là trong trường hợp $\rho\ge 0,0\le \theta <\frac{\pi}{2}$. Với các giá trị này của $\rho$ và $\theta$ ta có: $\rho=a\sqrt{2}.\sqrt{cos 2\theta}$. Dễ dàng thấy rằng ở đây $\theta$ chỉ có thể biến đổi giữa các giá trị $\theta=0$ và $\theta=\frac{\pi}{4}$. Vì vậy phần tương ứng của đường nằm trong góc giữa trục cực và tia $\theta=\frac{\pi}{4}$. Nếu $\theta=0$ thì $\rho=a\sqrt{2}$. Khi $\theta$ tăng từ $0$ đến $\frac{\pi}{4}$ đại lượng $\rho$ giảm dần đến giá trị $\rho=0$.

Sử dụng tính đối xứng ta có thể vẽ được đường lemniscat (h.2)

Hình 2.

41. Lập phương trình quỹ tích các điểm cách đều hai điểm $A(1;1)$ và $B(3;3)$.

Giải. Giả sử điểm $M$ nằm trên đường cần tìm, khi đó $|MA|=|MB|$. Theo công thức tính khoảng cách giữa hai điểm ta được:

$|MA|=\sqrt{(x-1)^2+(y-1)^2},|MB|=\sqrt{(x-3)^2+(y-3)^2}$

và phương trình của đường có thể viết dưới dạng $\sqrt{(x-1)^2+(y-1)^2}=\sqrt{(x-3)^2+(y-3)^2}$.

Sau khi bình phương cả hai vế đẳng thức trên ta được:

$x^2-2x+1+y^2-2y+1=x^2-6x+9+y^2-6y+9$.

Rút gọn các số hạng đồng dạng, cuối cùng ta đi tới phương trình: $x+y-4=0$.

42. Điểm $M$ chuyển động đều theo một tia quay đều quanh cực. Lập phương trình của đường vạch ra bởi điểm $M$, nếu tại thời điểm ban đầu tia quay trùng với trục cực còn điểm $M$ trùng với cực; khi quay tia đến góc $\theta=1(\text{ một radian })$ điểm $M$ cách cực một khoảng là $a$.

Giải. Vì tại thời điểm ban đầu $\rho$ và $\theta$ đều bằng không và sau đó cả hai đều tăng, tỷ lệ với thời gian nên dễ dàng thấy rằng, chúng phụ thuộc với nhau theo tỷ lệ thuận: $\frac{\rho}{\theta}=\text{const}$. Nhưng khi $\theta=1$ thì $\rho=a$ nên $\frac{\rho}{\theta}=\frac{a}{1}$, nghĩa là $\rho=a\theta$. Đường $\rho=a\theta$ được gọi là đường xoắn $Acsimet$.

43.Đường tròn đường kính $a$ lăn không trượt ở phía ngoài một đường khác có cùng đường kính. Lập phương trình trong tọa độ cực của đường được vạch ra bởi một điểm cố định nào đó của đường tròn lăn.

Hình 3.

Giải. Trên hình 3. $C_1$ là vị trí ban đầu của tâm đường tròn lăn; $A$ là vị trí ban đầu của điểm vạch ra đường cần tìm (điểm $A$ đối kính với điểm $B$- điểm tiếp xúc của hai đường tròn tại thời điểm ban đầu); $C_2$ là tâm của đường tròn bất động; $C_3$ là tâm của đường tròn lăn tại vị trí mới; $M$ là vị trí mới của điểm $A$, vạch ra đường cần tìm. (Sau khi di chuyển đường tròn $C_1$ đến vị trí $C_3$ điểm $P$ chiếm vị trí $Q$, điểm $B$ chiếm vị trí $D$, trong đó, vì lăn không trượt nên $\overarc{BQ}=\overarc{DQ},\angle{QC_2B}=\angle{QC_3D}$).

  Trên hình vẽ đã chỉ ra vị trí cực $O$ và trục cực $Ox$. Cần lập phương trình mà các tọa độ của điểm $M(\rho;\theta)$ bất kỳ trên đường cần tìm phải thỏa mãn.

Dễ dàng thấy rằng $\angle{MC_3Q}=\angle{OC_2Q}$, do đó tứ giác $OC_2C_3M$ là hình thang cân với đáy nhỏ $|C_2C_3|=a;C_2C_2'$ và $C_3C_3'$ là các đường thẳng góc hạ từ các điểm $C_2$ và $C_3$ lên đường thẳng $OM$. Vậy

$\rho=|OC_2'|+|C_2'C_3'|+|C_3'M|=\frac{a}{2}cos\theta+a+\frac{a}{2}cos\theta=a(1+cos\theta)$.

Vì vậy phương trình của đường cần tìm trong tọa độ cực có dạng $\rho=a(1+cos\theta)$; nó là đường cacđiôit.

Vì khi thay $\theta$ bằng $-\theta$ phương trình cacđiôit không thay đổi, nên đường cacđiôit đối xứng qua trục cực.

44. Tìm phương trình quỹ tích các điểm cách đều hai điểm $A(2;0)$ và $B(0;1)$.

45. Phương trình $x=y$ xác định đường nào?

46. Phương trình $x=-y$ xác định đường nào?

47. Lập phương trình quỹ tích các điểm mà tổng các bình phương các khoảng cách từ chúng đến các điểm $A(2;0)$ và $B(0;2)$ bằng bình phương khoảng cách giữa các điểm $A$ và $B$.

48. Lập phương trình quỹ tích các điểm mà tổng khoảng cách từ chúng đến các điểm $A(1;0)$ và $B(0;1)$ bằng $2$.

49. Lập phương trình trong hệ tọa độ cực của đường tròn có tâm tại cực.

50. Lập phương trình trong hệ tọa độ cực của nửa đường thẳng đi qua cực và tạo với trục cực góc $\alpha$.

51. Lập phương trình trong hệ tọa độ cực của đường tròn đường kính $\alpha$, nếu cực nằm trên đường tròn và trục cực đi qua tâm đường tròn.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 01-02-2019 - 18:06

[tritanngo99]

5) Phương trình tham số của đường. 

Để tìm phương trình quỹ tích (đường), cho thuận lợi hơn đôi khi ta biểu diễn các tọa độ $x$ và $y$ của điểm tùy ý của quỹ tích này qua một đại lượng phụ $t$ nào đó( nó được gọi là tham số), nghĩa là biểu diễn $x$ và $y$ dưới dạng: $\left\{\begin{array}{I} x=\phi(t)\\ y=\Phi(t)\end{array}\right.$

 Cách biểu diễn đường cần tìm như thế được gọi là biểu diễn bằng tham số, còn các phương trình của hệ được gọi là các phương trình tham số của đường đã cho.

  Khử tham số $t$ từ hệ (nếu có thể được) ta dẫn tới phương trình liên hệ $x$ và $y$, nghĩa là dẫn tới phương trình thông thường của đường dạng $f(x,y)=0$.

Các ví dụ: 

52. Tìm phương trình tham số của đường tròn..

Giải. Ta xét đường tròn bán kính $a$ với tâm tại gốc tọa độ (h.4). Ta lấy điểm $M(x;y)$ bất kỳ trên nó. Chọn góc giữa trục hoành với bán kính $OM$ là tham số $t$.

Hình 4.

Từ tam giác $OMN$ suy ra $x=acos(t),y=asin(t)$.

Vì vậy các phương trình: $\left\{\begin{array}{I} x=acos(t)\\ y=asin(t)\end{array}\right.$ là các phương trình tham số của đường tròn.

Khử tham số $t$ từ các phương trình này ta được phương trình thông thường của đường tròn. Để khử tham số trong trường hợp này cần bình phương từng phương trình rồi cộng các phương trình nhận được: $x^2=a^2cos^2(t);y^2=a^2sin^2(t)\implies x^2+y^2=a^2$.

Phương trình cuối cùng là phương trình đường tròn bán kính $a$ với tâm tại gốc tọa độ.

53. Lập phương trình tham số của đường vạch ra bởi một điểm cố định của một đường tròn lăn không trượt trên một đường thẳng bất động.

Hình 5..

Giải. Giả sử đường tròn bán kính $a$ lăn không trượt về phía phải trên đường thẳng nằm ngang (h.5). Ta lấy đường thẳng này làm trục $Ox$ và chọn gốc tọa độ tại một điểm $O$ nào đấy của trục. Ta lấy điểm trùng với điểm $O$ tại vị trí tương ứng của đường tròn làm điểm cố định trên đường tròn( mà khi di chuyển nó vạch ra đường cần tìm). Ta lấy góc quay của bán kính đường tròn đi qua điểm cố định làm tham số $t$.

 Giả sử tại thời điểm nào đó đường tròn tiếp xúc với trục tại điểm $A$. Điểm cố định của đường tròn chiếm vị trí $M(x;y)$ tương ứng với góc quay $t$ của bán kính $CM(t=\angle{ACM})$. Vì lăn không trượt nên $|OA|=\overarc{MA}=at$. Sử dụng đẳng thức này ta biểu diễn các tọa độ của điểm $M$ qua $t:$

$x=|ON|=|OA|-|NA|=\overline{MA}-|NA|=at-asin(t)=a(t-sin(t))$,

$y=|NM|=|AP|=|AC|-|PC|=a-acos(t)=a(1-cos(t))$.

  Vì vậy phương trình tham số của đường cần tìm là: $\left\{\begin{array} x=a(t-sin(t))\\ y=a(1-cos(t))\end{array}\right.$ 

Đường này gọi là đường xiclôit; nó được biểu diễn trên hình 5.

54. Các phương trình tham số $x=t^2,y=t^2$ xác định đường nào?

Giải. Khử tham số $t$ ta dẫn tới phương trình $y=x$. Nhưng theo các phương trình tham số thì $x\ge 0,y\ge 0$. Do đó các phương trình tham số đã cho xác định một tia hướng theo đường phân giác của góc tọa độ thứ nhất.

55. Các phương trình tham số: $\left\{\begin{array}{I} x=cos(t)\\ y=cos^2(t)\end{array}\right.$ xác định đường nào?

Giải. Trong phương trình thứ hai thay $cos(t)$ bằng $x$ ta được phương trình đường parabôn $y=x^2$. Từ các phương trình tham số suy ra $|x|\le 1,0\le y\le 1$. Vì vậy các phương trình tham số xác định cung $AOB$ của đường parabôn $y=x^2$, trong đó: $A(-1;-1),B(1;1)$.

56. Các phương trình: $\left\{\begin{array}{I} x=sin(t)\\ y=cosec(t)=\frac{1}{sin(t)}\end{array}\right.$ xác định đường nào?

Giải. Vì $y=\frac{1}{sin(t)}$ nên khử $t$ ta được phương trình $y=\frac{1}{x}$ biểu thị sự phụ thuộc tỷ lệ nghịch của các đại lượng $x$ và $y$.

Chú ý rằng: $|x|\le 1,|y|\ge 1$, ta kết luận đường cong cho bởi các phương trình tham số $x=sin(t),y=cosec(t)$ có dạng như trong hình $6$.

Hình 6.

57. Các phương trình $x=2t,y=4t$ xác định đường nào?

58. Đường cong cho bởi các phương trình tham số $\left\{\begin{array}{I} x=acos(t)\\ y=bsin(t)\end{array}\right.$ 

Tìm phương trình đường này trong hệ tọa độ vuông góc.

Hướng dẫn. Chia phương trình đầu cho $a$, phương trình thứ hai cho $b$, sau đó khử $t$.

59. Đường cong cho bởi phương trình tham số: $\left\{\begin{array}{I} x=asec(t)\\y=btan(t)\end{array}\right.$

Tìm phương trình của đường cong trong hệ tọa độ vuông góc.

60. Các phương trình $\left\{\begin{array}{I} x=cos^2(t)\\ y=sin^2(t)\end{array}\right.$ xác định đường nào?

61. Đường cong xác đinh bởi các phương trình tham số $\left\{\begin{array}{I} x=acos^3(t)\\y=asin^3(t)\end{array}\right.$ được gọi là đường axtrôit. Hãy khử t để tìm phương trình của axtrôit trong hệ tọa độ vuông góc.

62. Ta quấn một sợi chỉ theo chiều kim đồng hồ quanh vòng tròn tâm $O$ bán kính $a$; giả sử đầu mút của sợi chỉ nằm tại điểm $A(a;0)$. Bắt đầu gỡ sợi chỉ ra khỏi vòng tròn (ngược chiều kim đồng hồ) và luôn luôn giữ căng từ đầu mút. Lập phương trình tham số của đường do đầu mút của sợi chỉ vạch ra, nếu lấy tham số $t$ là góc giữa bán kính $OA$ và bán kính $OB$ đi qua tiếp điểm của đường tròn với sợi chỉ căng tại vị trí bất kỳ của sợi chỉ.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 09-02-2019 - 06:19

[tritanngo99]

Phần 2: ĐƯỜNG THẲNG

1) Phương trình tổng quát của đường thẳng. 

Mọi phương trình bậc nhất đối với $x$ và $y$, nghĩa là phương trình dạng $Ax+By+C=0$,

(trong đó $A,B$ và $C$ là các hệ số không đổi và $A^2+B^2\ne 0$) xác định trên mặt phẳng một đường thẳng nào đó. Phương trình này được gọi là phương trình tổng quát của đường thẳng.

    CÁC TRƯỜNG HỢP ĐẶC BIỆT.

1. $C=0;A\ne 0;B\ne 0$. Đường thẳng xác định bởi phương trình $Ax+By=0$ đi qua gốc tọa độ.

2. $A=0;B\ne 0;C\ne 0$. Đường thẳng xác định bởi phương trình $By+C=0$( hoặc $y=b$, trong đó $b=-\frac{C}{B}$) song song với trục $Ox$.

3. $B=0;A\ne 0;C\ne 0$. Đường thẳng xác định bởi phương trình $Ax+C=0$( hoặc $x=a$, trong đó $a=-\frac{C}{A}$) song song với trục $Oy$.

4. $B=C=0;A\ne 0$. Đường thẳng xác định bởi phương trình $Ax=0$( hoặc $x=0$ vì $A\ne 0$) trùng với trục $Oy$.

5. $A=C=0;B\ne 0$. Đường thẳng xác định bởi phương trình $By=0$( hoặc $y=0$ vì $B\ne 0$) trùng với trục $Ox$.

[tritanngo99]

2) Phương trình đường thẳng với hệ số góc.

  Nếu trong phương trình tổng quát của đường thẳng mà $B\ne 0$ thì bằng cách giải nó theo $y$ ta được phương trình dạng $y=kx+b$ (ở đây $k=-\frac{A}{B},b=-\frac{C}{B}$). Phương trình này được gọi là phương trình với hệ số góc, vì trong đó $k=tan \alpha,\alpha$ là góc tạo nên bởi đường thẳng với hướng dương của trục $Ox$. Số hạng tự do $b$ của phương trình bằng tung độ của giao điểm của đường thẳng với trục $Oy$.

[tritanngo99]

3. Phương trình đoạn thẳng theo các đoạn chắn.

   Nếu trong phương trình tổng quát của đường thẳng mà $C\ne 0$ thì bằng cách chia tất cả các số hạng của nó cho $-C$ ta được phương trình dạng: $\frac{x}{a}+\frac{y}{b}=1$( ở đây $a=-\frac{C}{A},b=-\frac{C}{B}$). Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn: trong đó $a$ là hoành độ của giao độ của giao điểm của đường thẳng với trục $Ox$, còn $b$ là tung độ của giao điểm của đường thẳng với trục $Oy$.  Vì vậy $a$ và $b$ được gọi là các đoạn chắn trên các trục tọa độ.

[tritanngo99]

4) Phương trình dạng chuẩn của đường thẳng.

 Nếu nhân hai vế của phương trình tổng quát của đường thẳng $Ax+By+C=0$ với hệ số $\mu =\frac{1}{\pm \sqrt{A^2+B^2}}$( số này được gọi là thừa số chuẩn hóa), trong đó dấu trước căn cần chọn sao cho thỏa mãn điều kiện $\mu .C<0$ thì ta được phương trình: $x.cos \phi+y.sin \phi-p=0$.

 Phương trình này được gọi là là phương trình dạng chuẩn của đường thẳng. Ở đây $p$ là độ dài của đường thẳng hạ từ gốc tọa độ đến đường thẳng, còn $\phi$ là góc tạo nên bởi đường thẳng góc này với hướng dương của trục $Ox$.

Các ví dụ:

63. Lập phương trình đường thẳng chắn trên trục tung đoạn thẳng $b=-3$ và lập với hướng dương của trục hoành góc $\alpha=\frac{\pi}{6}$.

Giải. Tìm hệ số góc: $k=tan(\frac{\pi}{6})=\frac{1}{\sqrt{3}}$. Sử dụng phương trình đường thẳng hệ số góc ta được: $y=\frac{1}{\sqrt{3}}x-3$; bỏ mẫu số và chuyển tất cả các số hạng sang vế trái ta được phương trình tổng quát của đường thẳng $x-\sqrt{3}y-3\sqrt{3}=0$.

64. Lập phương trình đường thẳng chắn trên các trục tọa độ các đoạn $a=\frac{2}{5},b=-\frac{1}{10}$.

Giải. Sử dụng phương trình đường thẳng theo các đoạn chắn ta được: $\frac{x}{\frac{2}{5}}+\frac{y}{\frac{-1}{10}}=1$.

 Phương trình này có thể viết lại dưới dạng $\frac{5}{2}x-10y=1$ hoặc $5x-20y-2=0$ (Phương trình tổng quát của đường thẳng).

65. Cho phương trình tổng quát của đường thẳng $12x-5y-65=0$. Viết:

a) Phương trình với hệ số góc;

b) Phương trình theo các đoạn chắn.

c) Phương trình dạng chuẩn.

Giải. 

a) Giải phương trình đường thẳng đối với $y$ ta được phương trình với hệ số góc $y=\frac{12}{5}x-13$. Ở đây $k=\frac{12}{5},b=-13$.

b) Chuyển số hạng tự do của phương trình tổng quát sang vế phải và chia cả hai vế cho $65:\frac{12}{65}x-\frac{5}{65}y=1$. Viết lại phương trình cuối cùng dưới dạng: $\frac{x}{\frac{65}{12}}+\frac{y}{\frac{-65}{5}}=1$,

ta được phương trình đường thẳng đã cho theo các đoạn chắn.

Ở đây $a=\frac{65}{12},b=\frac{-65}{5}=-13$.

c) Ta xác định thừa số chuẩn hóa: $\mu =\frac{1}{\sqrt{12^2+(-5)^2}}=\frac{1}{13}$. Nhân cả hai vế của phương trình tổng quát với thừa số này ta được phương trình dạng chuẩn của đường thẳng $\frac{12}{13}x-\frac{5}{13}y-5=0$.

Ở đây $cos \phi=\frac{12}{13},sin \phi=\frac{-5}{13},p=5$.

66. Vẽ các đường thẳng:

a) $x-2y+5=0$

b) $2x+3y=0$

c) $5x-2=0$

d) $2y+7=0$.

Giải. a) Đặt $x=0$ vào phương trình ta được $y=\frac{5}{2}$. Do đó đường thẳng cắt trục tung tại điểm $B(0;\frac{5}{2})$.

Đặt $y=0$ ta được $x=-5$, nghĩa là giao điểm của đường thẳng với trục hoành là điểm $A(-5;0)$.

 Chỉ còn phải vẽ đường thẳng qua các điểm $A(-5;0)$ và $B(0;\frac{5}{2})$ (h.7).

Hình 7.

b) Đường thẳng $2x+3y=0$ đi qua gốc tọa độ vì trong phương trình của đường thẳng thiếu số hạng tự do. Cho $x$ một giá trị nào đó, chẳng hạn $x=3$, khi đó $6+3y=0$, nghĩa là $y=-2$. Ta được điểm $M(3;-2)$. Chỉ còn phải vẽ đường thẳng qua gốc tọa độ và điểm $M$.

c) Giải phương trình đường thẳng đối với $x$, ta được $x=\frac{2}{5}$. Đường thẳng này song song với trục tung và chắn trên trục hoành một đoạn thẳng bằng $\frac{2}{5}$.

d) Tương tự như trên ta được phương trình $y=\frac{-7}{2}$. Đường thẳng này song song với trục hoành.

67. Cho phương trình đường thẳng $\frac{x+2\sqrt{5}}{4}+\frac{y-2\sqrt{5}}{2}=0$.

Viết: 

a) Phương trình tổng quát của đường thẳng này

b) Phương trình với hệ số góc

c) Phương trình theo các đoạn chắn

d) Phương trình dạng chuẩn.

68. Đường thẳng $2x+2y-5=0$ lập với hướng dương của trục hoành một góc là bao nhiêu?

69. Tính diện tích tam giác tạo thành bởi đường thẳng $4x+3y-36=0$ với các trục tọa độ.

70. Phương trình đường thẳng $20x+21y=0$ có thể viết theo các đoạn chắn hay không?

71. Vẽ các đường thẳng:

a) $4x-5y+15=0$

b) $2x-y=0$

c) $7x-10=0$

d) $2y+3=0$

72. Lập phương trình đường thẳng chắn trên tung đoạn $b=1$ và lập với hướng dương của trục hoành góc $\alpha=\frac{2}{3}\pi$.

73. Đường thẳng chắc trên các trục tọa độ những đoạn thẳng dương và bằng nhau. Lập phương trình đường thẳng nếu diện tích của tam giác tạo nên bởi đường thẳng này với các trục tọa độ bằng $8$ đ.v.d.t

74. Lập phương trình đường thẳng đi qua gốc tọa độ và điểm $A(-2;-3)$.

75. Lập phương trình đường thẳng đi qua điểm $A(2;5)$ và chắn trên trục tung đoạn $b=7$.

76. Lập phương trình các đường thẳng đi qua điểm $M(-3;-4)$ và song song với các trục tọa độ.

77. Lập phương trình đường thẳng chắn trên các trục tọa độ những đoạn bằng nhau, nếu độ dài của đoạn đường thẳng giữa hai trục tọa độ bằng $5\sqrt{2}$.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 02-02-2019 - 08:00

[tritanngo99]

5) Góc giữa các đường thẳng. Phương trình đường thẳng đi qua hai điểm.

Góc nhọn giữa hai đường thẳng $y=k_1x+b_1$ và $y=k_2x+b_2$ được xác định theo công thức $tan \phi=|\frac{k_2-k_1}{1+k_1k_2}|\text{      (1)}$.

Điều kiện song song của các đường thẳng có dạng $k_1=k_2$.

Điều kiện thẳng góc của các đường thẳng có dạng $k_1=\frac{-1}{k_2}$.

Phương trình đường thẳng có hệ số góc $k$ và đi qua điểm $M(x_1;y_1)$ được viết dưới dạng: $y-y_1=k(x-x_1)\text{          (2)}$

Phương trình đường thẳng đi qua đi qua các điểm $M_1(x_1;y_1)$ và $M_2(x_2;y_2)$ được viết dưới dạng: $\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1},\text{       (3)}$

còn hệ số góc của đường thẳng này tính theo công thức: $k=\frac{y_2-y_1}{x_2-x_1},\text{       (4)}$

 Nếu $x_1=x_2$ thì phương trình đường thẳng đi qua các điểm $M_1$ và $M_2$ có dạng $x=x_1$

 Nếu $y_1=y_2$ thì phương trình đường thẳng đi qua các điểm $M_1$ và $M_2$ có dạng $y=y_1$

[tritanngo99]

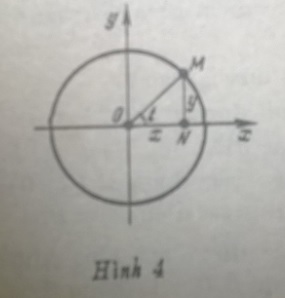
6. Giao điểm của các đường thẳng. Khoảng cách từ một điểm đến một đường thẳng. Chùm đường thẳng.

  Nếu $\frac{A_1}{A_2}\ne \frac{B_1}{B_2}$ thì các tọa độ của giao điểm các đường thẳng $A_1x+B_1y+C_1=0$ và $A_2x+B_2y+C_2=0$ tìm được bằng cách giải đồng thời các phương trình này.

  Khoảng cách từ điểm $M(x_0;y_0)$ đến đường thẳng $Ax+By+C=0$ được tính theo công thức: $d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$.

  Các đường phân giác của các góc giữa các đường thẳng $A_1x+B_1y+C_1=0$ và $A_2x+B_2y+C_2=0$ có phương trình: 

$\frac{A_1x+B_1y+C_1}{\sqrt{A_1^2+B_1^2}}\pm \frac{A_2x+B_2y+C_2}{\sqrt{A_2^2+B_2^2}}=0$.

  Nếu các đường thẳng cắt nhau cho bởi các phương trình $A_1x+B_1y+C_1=0$ và $A_2x+B_2y+C_2=0$ thì phương trình $A_1x+B_1y+C_1+\lambda(A_2x+B_2y+C_2)=0$, trong đó $\lambda$ là một thừa số, xác định đường thẳng đi qua giao điểm của các đường thẳng đã cho. Trong phương trình cuối cùng cho $\lambda$ các giá trị khác nhau ta sẽ được các đường thẳng khác nhau thuộc chùm đường thẳng có tâm tại giao điểm của các đường thẳng đã cho.

Các ví dụ:

78. Xác định góc giữa các đường thẳng $y=-3x+7$ và $y=2x+1$.

Giải: Đặt $k_1=-3,k_2=2$ trong công thức $(1)$ ta được: $tan \phi=|\frac{-(-3)+2}{1+(-3).2}|=1$, nghĩa là: $\phi=\frac{\pi}{4}$.

79. Chứng minh rằng các đường thẳng $4x-6y+7=0$ và $20x-30y-11=0$ song song.

Giải. Đưa phương trình của mỗi đường thẳng về dạng với hệ số góc ta được: $y=\frac{2}{3}x+\frac{7}{6}$ và $y=\frac{2}{3}x-\frac{11}{30}$.

Các hệ số góc của các đường thẳng này bằng nhau: $k_1=k_2=\frac{2}{3}$. Từ đó ta kết luận các đường thẳng đó song song.

80. Chứng minh rằng các đường thẳng $3x-5y+7=0$ và $10x+6y-3=0$ thẳng góc với nhau.

Giải. Sau khi đưa các phương trình về dạng với hệ số góc ta được: $y=\frac{3}{5}x+\frac{7}{5}$ và $y=\frac{-5}{3}x+\frac{1}{2}$. Ở đây $k_1=\frac{3}{5},k_2=\frac{-5}{3}$. Vì $k_1=-\frac{1}{k_2}$ nên các đường thẳng thẳng góc với nhau.

81. Lập phương trình đường thẳng đi qua các điểm $M(-1;3)$ và $N(2;5)$.

Giải. Đặt $x_1=-1,y_1=3,x_2=2,y_2=5$ trong phương trình $(3)$, mục $5$, ta được:

$\frac{y-3}{5-3}=\frac{x+1}{2+1}$ hay $\frac{y-3}{2}=\frac{x+1}{3}$.

 Vậy phương trình cần tìm có dạng $2x-3y+11=0$. Ta thử lại phương trình vừa lập là đúng. Muốn thế chỉ cần chứng tỏ rằng các tọa độ của các điểm $M$ và $N$ thỏa mãn phương trình đường thẳng. Thật vậy, các đường thẳng $2.(-1)-3.3+11=0,2.2-3.5+11=0$ được thỏa mãn một cách đồng nhất.

82. Lập phương trình đường thẳng đi qua các điểm $A(-2;4)$ và $B(-2;-1)$.

Giải. Vì $x_1=x_2=-2$ nên đường thẳng có phương trình $x=-2$ (song song với trục tung).

83. Chứng minh rằng các đường thẳng $3x-2y+1=0$ và $2x+5y-12=0$ cắt nhau và tìm các tọa độ của giao điểm.

Giải. Vì $\frac{3}{2}\ne \frac{-2}{5}$ nên các đường thẳng cắt nhau. Giải hệ phương trình: $\left\{\begin{array}{I} 3x-2y+1=0\\ 2x+5y-12\end{array}\right.$.

Ta được $x=1,y=2$, nghĩa là các đường thẳng cắt nhau tại điểm $(1;2)$.

84. Xác định khoảng cách từ điểm $M(x_0;y_0)$ đến đường thẳng $Ax+By+C=0$ mà không dùng phương trình dạng chuẩn của đường thẳng.

Giải. Bài toán được đưa về việc xác định khoảng cách giữa các điểm $M(x_0;y_0)$ và $N$, trong đó $N$ là chân đường vuông góc hạ từ điểm $M(x_0;y_0)$ đến đường thẳng $Ax+By+C=0$. Ta lập phương trình đường thẳng $MN$. Vì hệ số góc của đường thẳng đã cho bằng $\frac{-A}{B}$, nên hệ số góc của đường thẳng $MN$ bằng $\frac{A}{B}$ (từ điều kiện thẳng góc) và phương trình đường thẳng $MN$ có dạng $y-y_0=\frac{B}{A}(x-x_0)$. Phương trình này có thể viết dưới dạng: $\frac{x-x_0}{A}=\frac{y-y_0}{B}$.

 Để xác định các tọa độ của điểm $N$ ta giải hệ phương trình:

$Ax+By+C=0$ và $\frac{x-x_0}{A}=\frac{y-y_0}{B}$.

Ta đưa vào ẩn phụ $t: \frac{x-x_0}{A}=\frac{y-y_0}{B}=t$.

Khi đó $x-x_0+At,y=y_0+Bt$. Thay các giá trị này vào phương trình đã cho: $A(x_0+At)+B(y_0+Bt)+C=0$ ta tìm được: $t=-\frac{Ax_0+By_0+C}{A^2+B^2}$.

Thay giá trị của $t$ vào phương trình $x=x_0+At$ và $y=y_0+Bt$ ta xác định được các tọa độ của điểm $N$:

$x=x_0-A.\frac{Ax_0+By_0+C}{A^2+B^2},y=y_0-B.\frac{Ax_0+By_0+C}{A^2+B^2}$.

Còn phải xác định khoảng cách giữa các điểm $M$ và $N$ theo công thức: $d=\sqrt{(x-x_0)^2+(y-y_0)^2}$.

$=\sqrt{(A.\frac{Ax_0+By_0+C}{A^2+B^2})^2+(B.\frac{Ax_0+By_0+C}{A^2+B^2})^2}=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$.

85. Xác định khoảng cách từ điểm $M(1;2)$ đến đường thẳng $20x-21y-58=0$.

Giải. Ta có: $d=\frac{|20.1-21.2-58|}{\sqrt{400+441}}=\frac{|20-42-58|}{29}=\frac{|-80|}{29}=2\frac{22}{29}$.

86. Cho đường thẳng $l:4x-3y-7=0$. Điểm nào trong các điểm $A(2\frac{1}{2};1),B(3;2),C(1;-1),D(0;-2),E(4;3),F(5;2)$ nằm trên đường thẳng này?

Giải. Nếu điểm nằm trên đường thẳng, thì các tọa độ của nó phải thỏa mãn phương trình đường thẳng. Ta có:

$A\in l$ vì $4.\frac{5}{2}-3.1-7=0,B\notin l$ vì $4.3-3.2-7\ne 0$. Tương tự cho các điểm còn lại.

87. Lập phương trình đường thẳng đi qua điểm $M(-2;-5)$ và song song với đường thẳng $3x+4y+2=0$.

Giải. Ta giải phương trình đường thẳng đối với $y:y=\frac{-3}{4}x-\frac{1}{2}$. Do đó, theo điều kiện song song, hệ số góc của đường thẳng cần tìm bằng $\frac{-3}{4}$, Sử dụng phương trình $(2)$,mục $5$ ta được: $y-(-5)=\frac{-3}{4}[x-(-2)]$, nghĩa là $3x+4y+26=0$.

88. Cho các đỉnh của tam giác: $A(2;2),B(-2;-8)$ và $C(-6;-2)$. Lập phương trình các đường trung tuyến của tam giác.

Giải.Ta tìm tọa độ của điểm giữa của các cạnh $BC,AC$ và $AB$.

$x'=\frac{-2-6}{2}=-4,y'=\frac{-8-2}{2}=-5;A_1(-4;-5)$.

$x''=\frac{2-6}{-2}=-2,y''=\frac{2-2}{2}=0;B_1(-2;0)$.

$x'''=\frac{2-2}{2}=0,y'''=\frac{2-8}{2}=-3;C_1(0;-3)$.

 Phương trình các đường trung tuyến tìm được nhờ phương trình đường thẳng đi qua hai điểm cho trước. Phương trình đường trung tuyến $AA_1:\frac{y-2}{-5-2}=\frac{x-2}{-4-2}$, hay $\frac{y-2}{7}=\frac{x-2}{6}$, tức là: $7x-6y-2=0$.

Ta tìm phương trình đường trung tuyến $BB_1$; vì các điểm $B(-2;-8)$ và $B_1(-2;0)$ có hoành độ nên trung tuyến $BB_1$ song song với trục tung. Phương trình của nó là $x+2=0$.

Phương trình đường trung tuyến $CC_1:\frac{y+2}{-3+2}=\frac{x+6}{0+6}$, hay $x+6y+18=0$.

89. Cho các đỉnh của tam giác $A(0;1),B(6;5)$ và $C(12;-1)$. Lập phương trình đường cao của tam giác hạ từ đỉnh $C$.

Giải. Theo công thức $(4)$ ta tìm hệ số góc của cạnh $AB:k=\frac{5-1}{6-0}=\frac{4}{6}=\frac{2}{3}$.

Theo điều kiện thẳng góc, hệ số góc của đường cao hạ từ đỉnh $C$ bằng $-\frac{3}{2}$.

Phương trình đường cao này có dạng: $y+1=\frac{-3}{2}(x-12)$ hay $3x+2y-34=0$.

90. Cho các cạnh của tam giác: $x+3y-7=0(AB),4x-y-2=0(BC),6x+8y-35=0(AC)$. Tìm độ dài của đường cao hạ từ đỉnh $B$.

Giải. Ta hãy xác định tọa độ của điểm $B$. Giải hệ phương trình: $x+3y-7=0$ và $4x-y-2=0$ ta được: $x=1,y=2$, nghĩa là $B(1;2)$. Ta tìm độ dài đường cao $BB_1$ theo công thức tính khoảng cách, từ điểm $B$ đến đường thẳng $AC$. Ta có: $|BB_1|=\frac{|6.1+8.2-35|}{\sqrt{6^2+8^2}}=1,3$.

91. Xác định khoảng cách giữa các đường thẳng song song $3x+y-3\sqrt{10}=0$ và $6x+2y+5\sqrt{10}=0$.

Giải. Bài toán được đưa về việc xác định khoảng cách từ một điểm tùy ý của một đường thẳng đến đường thẳng kia, chẳng hạn, đặt $x=0$ trong phương trình của đường thẳng đầu, ta được: $y=3\sqrt{10}$.

  Vì vậy $M(0;3\sqrt{10})$ là điểm nằm trên đường thẳng đầu. Ta xác định khoảng cách từ nó đến đường thẳng thứ hai: $d=\frac{|6.0+2.3\sqrt{10}+5\sqrt{10}|}{\sqrt{36+4}}=\frac{11\sqrt{10}}{2\sqrt{10}}=5,5$.

92. Lập phương trình các đường phân giác của góc giữa các đường thẳng $x+y-5=0$ và $7x-y-19=0(h.8)$.

Giải. Đầu tiên ta giải bài toán này dưới dạng tổng quát.

Như đã biết đường phân giác của các góc lập bởi hai đường thẳng là quỹ tích các điểm cách đều các đường thẳng ấy. Nếu phương trình của các đường thẳng đã cho là $A_1x+B_1y+C_1=0$ và $A_2x+B_2y+C_2=0(\frac{A_1}{A_2}\ne \frac{B_1}{B_2},$ nghĩa là các đường thẳng không song song $)$ thì với mỗi điểm $M(\overline{x};\overline{y})$ nằm trên một trong các đường phân giác ta có (dùng công thức tính khoảng cách từ một điểm đến một đường thẳng): 

$\frac{|A_1\overline{x}+B_1\overline{y}+C_1|}{\sqrt{A_1^2+B_1^2}}=\frac{|A_2\overline{x}+B_2\overline{y}+C_2|}{\sqrt{A_2^2+B_2^2}}$.

Hình 8.

Vì $M(\overline{x};\overline{y})$ là điểm bất kỳ của các đường phân giác nên nó có thể ký hiệu là $M(x;y)$ cho đơn giản. Chú ý rằng các biểu thức trong đẳng thức cuối cùng dưới dấu trị tuyệt đối có thể có các dấu khác nhau, đối với một trong các đường phân giác ta được phương trình: $\frac{A_1x+B_1y+C_1}{\sqrt{A_1^2+B_1^2}}=\frac{A_2x+B_2y+C_2}{\sqrt{A_2^2+B_2^2}}$, và đối với đường phân giác kia ta có phương trình: $\frac{A_1x+B_1y+C_1}{\sqrt{A_1^2+B_1^2}}=-\frac{A_2x+B_2y+C_2}{\sqrt{A_2^2+B_2^2}}$.

Vì vậy phương trình của cả hai đường phân giác có thể viết dưới dạng: $\frac{A_1x+B_1y+C_1}{\sqrt{A_1^2+B_1^2}}\pm \frac{A_2x+B_2y+C_2}{\sqrt{A_2^2+B_2^2}}=0$.

Bây giờ ta giải bài toán cụ thể đã đặt ra. Thay $A_1,B_1,C_1,A_2,B_2,C_2$ bằng các giá trị của chúng từ các phương trình đã cho ta được:

$\frac{x+y-5}{\sqrt{1+1}}\pm \frac{7x-y-19}{\sqrt{49+1}}=0$, nghĩa là $5(x+y-5)\pm (7x-y-19)=0$ .

Phương trình đường phân giác thứ nhất là $5(x+y-5)+(7x-y-19)=0$ nghĩa là $3x+y-11=0$. Phương trình đường phân giác thứ hai là $5(x+y-5)-(7x-y-19)=0$, nghĩa là $x-3y+3=0$.

93. Cho các đỉnh của tam giác: $A(1;1),B(10;13),C(13;6)$. Lập phương trình đường phân giác của góc $A$.

Giải. Ta dùng phương pháp khác để lập phương trình đường phân giác (so với phương pháp giải bài toán trên).

Giả sử $D$ là giao điểm của đường phân giác với cạnh $BC$. Từ tính chất của đường phân giác trong của tam giác ta suy ra rằng $\frac{|BD|}{|DC|}=\frac{|AB|}{|AC|}$. Nhưng : $|AB|=\sqrt{(10-1)^2+(13-1)^2}=15,|AC|=\sqrt{(13-1)^2+(6-1)^2}=13$.

Do đó: $\lambda=\frac{|BD|}{|DC|}=\frac{15}{13}$. Vì đã biết tỷ số do điểm $D$ chia đoạn $BC$ nên các tọa độ điểm $D$ được xác định bởi các đẳng thức. $x=\frac{10+\frac{15}{13}.13}{1+\frac{15}{13}},y=\frac{13+\frac{15}{13}.6}{1+\frac{15}{13}}$.

hoặc: $x=\frac{325}{28},y=\frac{259}{28}$,nghĩa là $D(\frac{325}{28};\frac{259}{28})$.

  Bài toán được đưa về lập phương trình đường thẳng đi qua các điểm $A$ và $D$: $\frac{y-1}{\frac{259}{28}-1}=\frac{x-1}{\frac{325}{28}-1}$, nghĩa là: $7x-9y+2=0$.

94. Cho phương trình các đường cao của tam giác $ABC:x+y-2=0;9x-3y-4=0$ và các tọa độ của đỉnh $A(2;2)$. Lập phương trình các cạnh của tam giác.

Giải. Dễ dàng thấy rằng đỉnh $A$ không nằm trên các đường thẳng đã cho: các tọa độ của nó không thỏa mãn phương trình của các đường cao này.

Giả sử $9x-3y-4=0$ là đường cao $BB_1$ và $x+y-2=0$ là phương trình đường cao $CC_1$. Ta lập phương trình cạnh $AC$, xem nó như đường thẳng đi qua điểm $A$ và thẳng góc với đường cao $BB_1$. Vì hệ số góc của đường cao $BB_1$ bằng $3$ nên hệ số góc của cạnh $AC$ bằng $\frac{-1}{3}$, nghĩa là $k_{AC}=\frac{-1}{3}$. Sử dụng phương trình đường thẳng đi qua một điểm cho trước và có hệ số góc cho trước ta được phương trình cạnh $AC:y-2=\frac{-1}{3}(x-2)$ hoặc $x+3y-8=0$. Tương tự ta được: $k_{CC_1}=-1,k_{AB}=1$ và cạnh $AB$ được xác định bởi phương trình $y-2=x-2$, nghĩa là $y=x$.

Giải đồng thời các phương trình của các đường thẳng $AB$ và $BB_1$ cũng như của các đường thẳng $AC$ và $CC_1$ ta tìm được các tọa độ của các đỉnh $B$ và $C$ của tam giác: $B(\frac{2}{3};\frac{2}{3})$ và $C(-1;3)$. Còn phải thiết lập phương trình cạnh $BC$.

$\frac{y-\frac{2}{3}}{3-\frac{2}{3}}=\frac{x-\frac{2}{3}}{-1-\frac{2}{3}}$, nghĩa là $7x+5y-8=0$.

95. Lập phương trình các đường thẳng đi qua điểm $M(5;1)$ và tạo với đường thẳng $2x+y-4=0$ góc $\frac{\pi}{4}$(h.9).

Giải: Giải sử hệ số góc của một trong các đường thẳng cần tìm bằng $k$. Hệ số góc của đường thẳng đã cho bằng $-2$. Vì góc giữa các đường thẳng này bằng $\frac{\pi}{4}$ nên $tan(\frac{\pi}{4})=|\frac{k+2}{1-2k}|$ hay $1=|\frac{k+2}{1-2k}|$.

từ đó $\frac{k+2}{1-2k}=1$ và $\frac{k+2}{1-2k}=-1$.

Giải các phương tình nhận được ta có $k=\frac{-1}{3}$ và $k=3$.

Vì vậy phương trình của một trong những đường thẳng phải tìm có dạng: $y-1=\frac{-1}{3}(x-5)$, nghĩa là $x+3y-8=0$, còn phương trình kia có dạng: $y-1=3(x-5)$, nghĩa là $3x-y-14=0$.

96. Tìm đường thẳng thuộc chùm $2x+3y+5+\lambda(x+8y+6)=0$ và đi qua điểm $M(1;1)$.

Giải. Các tọa độ của điểm $M$ phải thỏa mãn phương trình đường thẳng cần tìm, vì vậy để xác định $\lambda$ ta có phương trình: $2.1+3.1+5+\lambda(1+8.1+6)=0$

hoặc $10+15\lambda=0$, nghĩa là $\lambda=\frac{-2}{3}$.

Thay giá trị của $\lambda$ vào phương trình của chùm ta được phương trình đường thẳng $2x+3y+5-\frac{2}{3}(x+8y+6)=0$ hay $4x-7y+3=0$.  

97. Tìm đường thẳng đi qua giao điểm của các đường thẳng $3x-4y+7=0$ và $5x+2y+3=0$ và song song với trục tung.

Giải. Đường thẳng thuộc chùm $3x-4y+7+\lambda(5x+2y+3)=0$; tức là $(3+5\lambda)x+(-4+2\lambda)y+(7+3\lambda)=0$. Vì $y$ phải bằng $0:-4+2\lambda=0$, nghĩa là $\lambda=2$.

Thay giá trị tìm được của $\lambda$ vào phương trình của chùm ta được phương trình cần tìm $x+1=0$.

98. Cho các cạnh của tam giác: $x+2y+5=0(AB),3x+y+1=0(BC)$ và $x+y+7=0(AC)$. Lập phương trình đường cao của tam giác hạ xuống cạnh $AC$.

Giải. Đường cao thuộc chùm $x+2y+5+\lambda(3x+y+1)=0$ hay là $(1+3\lambda)x+(2+\lambda)y+(5+\lambda)=0$. Hệ số góc của đường thẳng thuộc chùm bằng $-\frac{1+3\lambda}{2+\lambda}$; vì hệ số góc của đường thẳng $AC$ bằng $-1$ nên hệ số góc của đường cao cần tìm bằng $1$ và để xác định $\lambda$ ta có phương trình: $-\frac{1+3\lambda}{2+\lambda}=1$.

Do đó $1+3\lambda+2+\lambda=0$, nghĩa là $\lambda=\frac{-3}{4}$. Thay giá trị tìm được của $\lambda$ vào phương trình của chùm ta được phương trình đường cao $(1-\frac{9}{4})x+(2-\frac{3}{4})y+(5-\frac{3}{4})=0$, nghĩa là $5x-5y-17=0$.

99. Cho các đỉnh của tan giác $ABC:A(0;2),B(7;3)$ và $C(1;6)$. Xác định $\angle{BAC}=\alpha$.

100. Cho các cạnh của tam giác: $x+y-6=0,3x-5y+14=0$ và $5x-3y-14=0$. Lập phương trình đường cao của tam giác.

101. Lập phương trình các đường phân giác của các góc giữa các đường thẳng $3x+4y-20=0$ và $8x+6y-5=0$.

102. Cho các đỉnh của tam giác: $A(0;0),B(-1;-3)$ và $C(-5;-1)$. Lập phương trình các đường thẳng đi qua các đỉnh và song song với các cạnh của tam giác.

103. Lập phương trình các đường thẳng đi qua điểm $M(2;7)$ và tạo với đường thẳng đi qua điểm $A(-1;7)$ và $B(8;-2)$ các góc $45^0$.

104. Tìm khoảng cách từ điểm $M(2;-1)$ đến đường thẳng chắn trên các trục tọa độ các đoạn $a=8,b=6$.

105. Cho tam giác vởi các đỉnh $A(\frac{3}{2};1),B(1;1\frac{2}{3}),C(3;3)$, tìm độ dài đường cao hạ từ đỉnh $C$.

106. Với giá trị nào của $m$ các đường thẳng $7x-2y-5=0,x+7y-8=0$ và $mx+my-8=0$ cắt nhau tại một điểm?

107. Cho điểm giữa các cạnh của tam giác $A_1(-1;-1),B_1(1;9)$ và $C_1(9;1)$. Lập phương trình các đường trung trực của tam giác.

108. Tìm góc nhọn tạo ra bởi trục tung và đường thẳng đi qua các điểm $A(2;\sqrt{3})$ và $B(3;2\sqrt{3})$.

109. Các điểm $A(1;2)$ và $C(3;6)$ là các đỉnh nối của hình vuông. Xác định các tọa độ hai đỉnh kia của hình vuông đó.

110. Tìm điểm trên trục hoành mà khoảng cách từ nó đến đường thẳng $8x+15y+10=0$ bằng $1$.

111. Cho các đỉnh của tam giác: $A(1;1),B(4;5)$ và $C(13;-4)$. Lập phương trình đường trung tuyến vẽ từ đỉnh $B$ và đường cao hạ từ đỉnh $C$. Tính diện tích tam giác.

112. Tìm các đường thẳng thuộc chùm $2x+3y+6+\lambda(x-5y-6)=0$ và thẳng góc với các đường thẳng cơ sở của chùm.

113. Tìm đường thẳng đi qua giao điểm của các đường thẳng $x+6y+5=0,3x-2y+1=0$ và điểm $M(\frac{-4}{5};1)$.

114. Tim đường thẳng đi qua giao điểm của các đường thẳng $x+2y+3=0,2x+3y+4=0$ và song song với đường thẳng $5x+8y=0$.

115. Tìm đường thẳng đi qua giao điểm của các đường thẳng $3x-y-1=0,x+3y+1=0$ và song song với trục hoành.

116. Tìm đường thẳng đi qua giao điểm của các đường thẳng $5x+3y+10=0,x+y-15=0$ và qua gốc tọa độ.

117. Tìm đường thẳng đi qua giao điểm của các đường thẳng $x+2y+1=0,2x+y+2=0$ và tạo với trục hoành góc $135^0$.

118. Lập phương trình các đường thẳng đi qua điểm $M(a;b)$ và tạo với đường thẳng $x+y+c=0$ góc $45^0$

119. Cho các cạnh của tam giác $x-y=0(AB),x+y-2=0(BC),y=0(AC)$. Lập phương trình đường trung tuyến đi qua đỉnh $B$ và đường cao đi qua đỉnh $A$.

120. Chứng minh rằng tam giác với cạnh $x+y\sqrt{3}+1=0,x\sqrt{3}+y+1=0$ và $x-y-10=0$ là cân. Tìm góc tại đỉnh của tam giác đó.

121. Cho các đỉnh liên tiếp của hình bình hành: $A(0;0),B(1;3),C(7;1)$. Tìm góc giữa các đường chéo của nó và chứng minh rằng hình bình hành này là hình chữ nhật.

122. Cho các cạnh của tam giác: $x-y+2=0(AB),x=2(BC),x+y-2=0(CA)$. Lập phương trình đường thẳng đi qua đỉnh $B$ và qua điểm trên cạnh $AC$, chia nó theo tỷ số $1:3$( tính từ đỉnh $A$).

123. Chứng minh rằng tam giác với các đỉnh $A(1;1),B(2;1+\sqrt{3}),C(3;1)$ là đều và tính diện tích của nó.

124. Chứng minh rằng tam giác có các cạnh cho bằng các phương trình với các hệ số nguyên không thể là tam giác đều.

125. Cho đỉnh $A(3;9)$ và phương trình các đường trung tuyến của tam giác $y-6=0$ và $3x-4y+9=0$. Tìm tọa độ hai đỉnh kia.

126. Lập phương trình cạnh huyền đi qua điểm $M(2;3)$ của tam giác vuông, nếu hai cạnh của góc vuông là hai trục tọa độ và diện tích tam giác bằng $12$(đ.v.d.t)

127. Lập phương trình ba cạnh của hình vuông, biết rằng cạnh thứ tư là một đoạn của đường thẳng $4x+3y-12=0$ mà các đầu mút của nó nằm trên các trục tọa độ.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 06-02-2019 - 06:35

[tritanngo99]

Phần 3: CÁC ĐƯỜNG BẬC HAI.

1) Đường tròn.

  Đường tròn là quỹ tích các điểm cách đều một điểm cho trước (tâm). Nếu $r$ là bán kính của đường tròn và điểm $C(a;b)$ là tâm của nó, thì phương trình đường tròn có dạng: $(x-a)^2+(y-b)^2=r^2(1)$

  Đặc biệt nếu tâm đường tròn trùng với gốc tọa độ thì phương trình cuối cùng có dạng: $x^2+y^2=r^2$.

 Nếu phá ngoặc trong vế trái của phương trình $(1)$, ta sẽ được phương trình dạng: $x^2+y^2+lx+my+n=0,(2)$

trong đó $l=-2a,m=-2b,n=a^2+b^2-r^2$.

  Trong trường hợp tổng quát phương trình $(2)$ xác định đường tròn nếu $l^2+m^2-4n>0$.

  Nếu $l^2+m^2-4n=0$ thì phương trình $(2)$ xác định điểm $(\frac{-l}{2};\frac{-m}{2})$, còn nếu $l^2+m^2-4n<0$ thì phương trình không có ý nghĩa hình học. Trong trường hợp đó người ta nói rằng phương trình xác định đường tròn ảo.

 Cần chú ý rằng phương trình đường tròn chứa các số hạng bậc cao $x^2$ và $y^2$ với các hệ số bằng nhau và không chứa số hạng là tích của $x$ và $y$.

  Vị trí tương đối của điểm $M(x_1;y_1)$ và đường tròn $x^2+y^2=r^2$ được xác định bởi các điều kiện sau: nếu $x_1^2+y_1^2=r^2$ thì điểm $M$ nằm trên đường tròn; nếu $x_1^2+y_1^2>r^2$ thì điểm $M$ nằm ngoài đường tròn và nếu $x_1^2+y_1^2<r^2$ thì điểm $M$ nằm trong đường tròn.

Các ví dụ: 

128. Tìm các tọa độ của tâm và bán kính của đường tròn $2x^2+2y^2-8x+5y-4=0$.

Giải. Chia phương trình cho $2$ và nhóm các số hạng, ta được $x^2-4x+y^2+\frac{5}{2}y=2$. Bổ sung $x^2-4x$ và $y^2+\frac{5}{2}y$ thành các chính phương bằng cách thêm $4$ vào nhị thức thứ nhất và $(\frac{5}{4})^2$ vào nhị thức thứ hai (đồng thời ở vế phải cũng thêm vào tổng của các số này): $(x^2-4x+4)+(y^2+\frac{5}{2}y+\frac{25}{16})=2+4+\frac{25}{16}$ hay $(x-2)^2+(y+\frac{5}{4})^2=\frac{121}{1.6}$.

 Vậy các tọa độ của tâm đường tròn là $a=2,b=\frac{-5}{4}$ và bán kính $r=\frac{11}{4}$.

129. Lập phương trình đường tròn ngoại tiếp tam giác có các cạnh cho bởi các phương trình $9x-2y-41=0,7x+4y+7=0,x-3y+1=0$.

Giải. Ta tìm các tọa độ của các đỉnh tam giác bằng cách giải ba hệ phương trình:

$\left\{\begin{array}{I} 9x-2y-41=0\\7x+4y+7=0 \end{array}\right.$,$\left\{\begin{array}{I} 9x-2y-41=0\\x-3y+1=0 \end{array}\right.$,$\left\{\begin{array}{I} 7x+4y+7=0\\x-3y+1=0 \end{array}\right.$

Ta được: $A(3;-7),B(5;2),C(-1;0)$.

 Giả sử phương trình đường tròn cần tìm có dạng $(x-a)^2+(y-b)^2=r^2$. Để tìm $a,b$ và $r$ ta viết ba đẳng thức bằng cách thay vào các tọa độ chạy trong phương trình cần tìm các tọa độ của các điểm $A,B$ và $C$: $(3-a)^2+(-7-b)^2=r^2;(5-a)^2+(2-b)^2=r^2;(-1-a)^2+b^2=r^2$.

Khử $r^2$ ta đi tới hệ phương trình: $\left\{\begin{array}{I} (3-a)^2+(-7-b)^2=(5-a)^2+(2-b)^2\\(3-a)^2+(-7-b)^2=(-1-a)^2+b^2 \end{array}\right.$
$\iff \left\{\begin{array}{I} 4a+18b=-29\\ 8a-14b=57 \end{array}\right.$. Do đó $a=3,1;b=-2,3$. Giá trị $r^2$ tìm được phương trình $(-1-a)^2+b^2=r^2$, nghĩa là$r^2=22,1$. Phương trình đường tròn cần tìm là: $(x-3,1)^2+(y+2,3)^2=22,1$.

130. Lập phương tròn đường tròn đi qua các điểm $A(5;0),B(1;4)$ và tâm của nó nằm trên đường thẳng $x+y-3=0$

Giải. Ta tìm tọa độ điểm giữa $M$ của dây cung $AB:x_M=\frac{5+1}{2}=3,y_M=\frac{4+0}{2}=2$, nghĩa là $M(3;2)$. Tâm đường tròn phải nằm trên trung trực của đoạn $[AB]$.

   Phương trình đường thẳng $AB$ có dạng: $\frac{y-0}{4-0}=\frac{x-5}{1-5}$ hay $x+y-5=0$.

Vì hệ số góc của đường thẳng này bằng $-1$, nên hệ số góc của đường thẳng góc là $k=1$ và phương trình của nó là $y-2=1.(x-3)$ hay $x-y-1=0$.

  Tâm $C$ của đường tròn nằm tại giao điểm của đường thẳng đã cho và đường thẳng góc, nghĩa là các tọa độ của tâm được xác định từ hệ phương trình $\left\{\begin{array}{I} x+y-5=0\\ x-y-1=0\end{array}\right.$.

Do đó $x=2,y=1$, nghĩa là $C(2;1)$.

  Bán kính đường tròn bằng độ dài đoạn $[CA]$, nghĩa là $r=\sqrt{(5-2)^2+(1-10)^2}=\sqrt{10}$. Vậy phương trình đường tròn là $(x-2)^2+(y-1)^2=10$.

131. Lập phương trình dây cung của đường tròn $x^2+y^2=49,$ được chia đôi tại điểm $A(1;2)$.

Giải. Ta lập phương trình đường kính của đường tròn đi qua điểm $A(1;2)$. Phương trình này là $y=2x$. Dây cung cần tìm thẳng góc với đường kính này và đi qua điểm $A$, do đó phương trình của nó là $y-2=\frac{-1}{2}(x-1)$ hay $x+2y-5=0$.

132. Tìm phương trình đường tròn đối xứng với đường tròn $x^2+y^2=2x+4y-4$ qua đường thẳng $x-y-3=0$.

Giải. Đưa phương trình đường tròn đã cho về dạng chính tắc $(x-1)^2+(y-2)^2=1$. Tâm đường tròn đã cho là điểm $C(1;2)$ và bán kính nó bằng $1$. Ta tìm các tọa độ của tâm $C_1(x_1;y_1)$ của đường tròn đối xứng, muốn thế qua điểm $C(1;2)$ ta vẽ đường thẳng góc với đường thẳng $x-y-3=0$; phương trình của nó là $y-2=k(x-1)$, trong đó $k=\frac{-1}{1}=-1$, suy ra $y-2=-x+1$ hay $x+y-3=0$. Giải đồng thởi hai phương trình $x-y-3=0$ và $x+y-3=0$ ta được $x=3,y=0$, nghĩa là hình chiếu của điểm $C(1;2)$ trên đường thẳng đã cho là điểm $P(3;0)$. Còn các tọa độ của điểm đối xứng ta nhận được theo công thức tính tọa độ điểm giữa của đoạn thẳng: $3=\frac{1+x_1}{2},0=\frac{2+y_1}{2}$; do đó $x_1=5,y_1=-2$. Vậy tâm đường tròn đối xứng là điểm $C_1(5;-2)$. Vì vậy phương trình đường tròn cần tìm là $(x-5)^2+(y+2)^2=1$.

133. Tìm quỹ tích điểm giữa các dây cung đi qua gốc tọa độ của đường tròn $x^2+y^2=4(y+1)$.

Giải. Phương trình các dây cung có dạng $y=kx$. Ta biểu diễn các tọa độ của các giao điểm của dây cung với đường tròn qua $k$. Muốn vậy, giải hệ $y=kx$ và $x^2+y^2-4y-4=0$, ta được phương trình bậc hai $x^2(k^2+1)-4kx-4=0$. Ở đây $x_1+x_2=\frac{4k}{k^2+1}$. Nhưng nửa tổng của các hoành độ này cho ta hoành độ của điểm giữa của dây cung, nghĩa là $x=\frac{2k}{1+k^2}$, còn tung độ của điểm giữa của dây cung $y=\frac{2k^2}{1+k^2}$. Hai phương trình cuối cùng là các phương trình tham số của quỹ tích cần tìm, khử $k$ (chỉ cần đặt $k=\frac{y}{x}$) vào phương trình $x=\frac{2k}{1+k^2}$ ta được phương trình của quỹ tích cần tìm $x^2+y^2-2y=0$. Vì vậy quỹ tích cần tìm cũng là đường tròn.

134. Xác định các tọa độ của tâm và bán kính của các đường tròn:

a) $x^2+y^2-8x+6y=0$

b) $x^2+y^2+10x-4y+29=0$

c) $x^2+y^2-4x+14y+54=0$

135. Tìm góc giữa các bán kính của đường tròn $x^2+y^2+4x-6y=0$ vẽ qua các giao điểm của đường tròn với $Oy$.

136. Lập phương trình đường tròn đi qua các điểm $A(1;2),B(0;-1),C(-3;0)$.

137. Lập phương trình đường tròn đi qua các điểm $A(7;7),B(-2;4)$ và tâm của nó trên đường thẳng $2x-y-2=0$.

138. Lập phương trình dây cung chung của các đường tròn $x^2+y^2=16$ và $(x-5)^2+y^2=9$.

139. Lập phương trình các tiếp tuyến với đường tròn $(x-3)^2+(y+2)^2=25$ kẻ từ các giao điểm của đường tròn này với đường thẳng $x-y+2=0$.

140. Cho đường tròn $x^2+y^2=4$. Từ điểm $A(-2;0)$ kẻ dây cung $AB$ rồi kéo dài ra một đoạn $|BM|=|AB|$. Tìm quỹ tích điểm $M$

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 07-02-2019 - 08:53

[tritanngo99]

2. Êlip

 Êlip là quỹ tích các điểm, mà tổng khoảng cách từ chúng đến hai điểm cho trước (được gọi là các tiêu điểm) là một đại lượng không đổi (thường được kí hiệu là $2a$), trong đó đại lượng không đổi này lớn hơn khoảng cách giữa hai tiêu điểm.

  Nếu đặt các trục tọa độ với eelip như trên hình $10$, còn các tiêu điểm của êlip nằm trên trục $Ox$ cách đều gốc tọa độ tại các điểm $F_1(c;0)$ và $F_2(-c;0)$ thì phương trình êlip có dạng đơn giản (dạng chính tắc) $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(1)$

  Ở đây $a$ là nửa trục lớn, $b$ là nửa trục nhỏ của êlip, trong đó $a,b$ và $c$ ($c$ là nửa khoảng cách giữa các tiêu điểm) liên hệ với nhau bởi hệ thức $a^2=b^2+c^2(c=\sqrt{a^2-b^2})$.

  Dạng của êlip (độ bẹt của nó) đặc trưng bởi tâm sai $e=\frac{c}{a}$ ( vì $c<a$ nên $e<1$).

  Khoảng cách từ điểm $M$ nào đó của êlip đến các tiêu điểm của nó được gọi là các vector bán kính tiêu của điểm này. Chúng thường được ký hiệu là $r_1$ và $r_2$ (theo định nghĩa của êlip, với mọi điểm của nó $r_1+r_2=2a$).

   Trong trường hợp đặc biệt $a=b(c=0,e=0)$, các tiêu điểm chập thành một điểm -tâm , êlip trở thành đường trong với phương trình $a^2+b^2=a^2$ .

  Vị trí tương đối của điểm $M(x_1;y_1)$ và êlip $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ được xác định bởi các điều kiện; 

nếu $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}=1$ thì điểm $M$ nằm trên êlip;

nếu $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}>1$ thì điểm $M$ nằm ngoài êlip;

nếu $\frac{x_1^2}{a^2}+\frac{y_1^2}{b^2}<1$ thì điểm $M$ nằm trong êlip.

Các vector bán kính tiêu được biểu diễn qua hoành độ của điểm trên êlip theo cồn thức $r_1=a-ex$ (vector bán kính tiêu phải) và $r_1=a+ex$ (vector bán kính tiêu trái).

Các ví dụ:

141. Lập phương trình chính tắc của êlip đi qua các điểm $M(\frac{5}{2};\frac{\sqrt{6}}{4})$ và $N(-2;\frac{\sqrt{15}}{5})$.

Giải. Giả sử phương trình cần tìm của êlip là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.

 Các tọa độ của các điểm đã cho phải thõa mãn phương trình này.

Do đó: $\frac{25}{4a^2}+\frac{3}{8b^2}=1$ và $\frac{4}{a^2}+\frac{3}{5b^2}=1$.

Suy ra $a^2=10,b^2=1$ và phương trình êlip có dạng $\frac{x^2}{10}+y^2=1$.

142. Trên êlip $\frac{x^2}{25}+\frac{y^2}{9}=1$ tìm điểm cí hiệu các vector bán kính tiêu bằng $\frac{32}{5}$.

143. Tìm độ dài đoạn thẳng thẳng góc với trục lớn của êlip $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ dựng từ tiêu điểm đến giao điểm với êlip.

144. Lập phương trình đường thẳng đi qua tiêu điểm trái và đỉnh dưới của êlip $\frac{x^2}{25}+\frac{y^2}{16}=1$.

145. Lập phương trình êlip đi qua điểm $M(1;1)$ và có tâm sai $e=\frac{3}{5}$.

146. Các điểm $M(7;1),N(-5;-4),P(4;5)$ có vị trí như thế nào đối với êlip $\frac{x^2}{50}+\frac{y^2}{32}=1$.

147. Tìm tâm sai của êlip nếu từ đỉnh trên nhìn thấy tiêu cự dưới một góc là $\alpha$.

148. Trên đường thẳng $x+5=0$ tìm điểm cách đều tiêu điểm trái và đỉnh trên của êlip $\frac{x^2}{20}+\frac{y^2}{4}=1$.

149. Sử dụng định nghĩa của êlip lập phương trình của nó biết rằng các điểm $F_1(0;0)$ và $F_2(1;1)$ là các tiêu điểm của êlip, còn độ dài của trục lớn bằng $2$.

150. Lập phương trình quỹ tích các điểm, mà khoảng cách của chúng tới điểm $A(0;1)$ hai lần bé hơn khoảng cách tới đường thẳng $y-4=0$.

151. Các mút của đoạn $AB$ độ dài $a$ không đổi trượt theo các cạnh của góc vuông. Tìm phương trình đường cong vẽ bởi điểm $M$ chia đoạn đó theo tỷ số $1:2$.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 07-02-2019 - 14:49

[tritanngo99]

3. Hypebôn.

  Hypebôn là quỹ tích các điểm, mà giá trị tuyệt đối của hiệu khoảng cách của chúng tới hai điểm cho trước( gọi là các tiêu điểm) là một đại lượng không đổi (kí hiệu là $2a$), hằng số đó bé hơn khoảng cách giữa các tiêu điểm. Đặt các tiêu điểm của hypebôn tại các điểm $F_1(c;0)$ và $F_2(-c;0)$ ta nhận được phương trình chính tắc của hypebôn $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(1)$. 

trong đó $b^2=c^2-a^2$. Hybebôn gồm hai nhánh và đối xứng qua các trục tọa độ. Các điểm $A_1(a;0)$ và $A_2(-a;0)$ gọi là các đỉnh của hypebôn, Đoạn $|A_1A_2|=2a$ gọi là trục thực của hypebôn, còn đoạn $|B_1B_2|=2b$ là trục ảo của nó (h.11).

  Đường thẳng được gọi là tiệm cận của hypebôn, nếu khoảng cách từ điểm $M(x;y)$ của hypebôn tới đường thẳng dần tới không khi $x\to +\infty$ hay $x\to -\infty$. hypebôn có hai tiệm cận: phương trình của chúng là $y=\pm \frac{b}{a}x$.

 Để dựng các tiệm cận của hypebôn ta dựng hình chữ nhật cơ sở của hybebôn với các cạnh $x=a,x=-a,y=b,y=-b$. Các đường thẳng đi qua các đỉnh đối diện của hình chữ nhật đó là các tiệm cận của hypebôn. Trên hình vẽ đã chỉ rõ vị trí của hypebôn và các tiệm cận của nó. Tỷ số $e=\frac{c}{a}>1$ gọi là tâm sai của hypebôn.

 Các vector bán kính tiêu của nhánh phải của hypebôn: $r_1=ex-a$( vector bán kính tiêu phải), $r_2=ex+a$( vector bán kính tiêu trái).

 Các vector bán kính tiêu của nhánh trái của hypebôn $r_1=-ex+a$ (vector bán kính tiêu phải), $r_2=-ex-a$ (vector bán kính tiêu trái).

 Nếu $a=b$ thì phương trình hypebôn có dạng $x^2-y^2=a^2$. Hypebôn này gọi là hypebôn đều. Các tiệm cận của nó lập thành góc vuông. Nếu lấy các tiệm cận của hypebôn đều làm các trục tọa độ, thì phương trình của nó có dạng: $xy=m(m=\pm \frac{a^2}{2})$, khi $m>0$ hypebôn nằm trong các góc phần tư thứ nhất và thứ ba, khi $m<0$- trong góc phần tư thứ hai và thứ tư. Vì phương trình $xy=m$ có thể viết dưới dạng $y=\frac{m}{x}$, nên hypebôn đều là đồ thị của sự phụ thuộc tỷ lệ nghịch giữa các đại lượng $x$ và $y$

  Phương trình $\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$ (hay $\frac{y^2}{b^2}-\frac{x^2}{a^2}=1$). (2).

cũng là phương trình hypebôn, nhưng trục thực của hypebôn này là một đoạn của trục $Oy$ độ dài $2b$.

  Hai hypebôn $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ và $\frac{x^2}{a^2}-\frac{y^2}{b^2}=-1$ có cùng các nửa trục và cùng các tiệm cận, nhưng trục thực của cái này là trục ảo của cái kia và ngược lại. Hai hypebôn như thế được gọi là liên hợp.

Các ví dụ:

152. Trên nhánh phải của hypebôn $\frac{x^2}{16}-\frac{y^2}{9}=1$, tìm điểm mà khoảng cách từ nó đến tiêu điểm phải bằng nửa khoảng cách từ nó đến tiêu điểm trái.

Giải. Đối với nhánh phải của hypebôn các vector bán kính tiêu được xác định theo công thức $r_1=ex-a$ và $r_2=ex+a$. Do đó ta có phương trình $ex+a=2(ex-a)$, suy ra: $x=\frac{3a}{e}$; ở đây $a=4,e=\frac{c}{a}=\frac{\sqrt{a^2+b^2}}{a}=\frac{\sqrt{16+9}}{4}=\frac{5}{4}$, nghĩa là $x=9,6$

 Ta tìm tung độ từ phương trình hypebôn:

$y=\pm \frac{3}{4}\sqrt{x^2-16}=\pm \frac{3}{4}\sqrt{(\frac{48}{5})^2-16}=\pm \frac{3}{5}\sqrt{119}$.

  Vì vậy có hai điểm thỏa mãn điều kiện của bài toán: $M_1(9,6;\frac{3}{5}\sqrt{119})$ và $M_2(9,6;\frac{-3}{5}\sqrt{119})$.

153. Cho các điểm $A(-1;0)$ và $B(2;0)$. Điểm $M$ chuyển động sao cho trong tam giác $AMB$ góc $B$ vẫn gấp đôi góc $A$. Tìm phương trình đường cong do điểm $M$ vạch ra.

Giải. Lấy điểm $M$ với các tọa độ $x$ và $y$, ta biểu diễn $tan(B)$ và $tan(A)$ qua tọa độ các điểm $A,B$ và $M$.

$tan(B)=-\frac{y}{x-2}=\frac{y}{2-x},tan(A)=\frac{y}{x+1}$.

Theo đầu bài ta có phương trình $tan(B)=tan(2A)$ (vì $B=2A$) hay tan(B)=\frac{2tan(A)}{1-tan(A)^2}. Thay trong đẳng thức này các biểu thức tìm được của $tan(A)$ và $tan(B)$ qua tọa độ điểm $M$, ta đi tới phương trình: $\frac{y}{2-x}=\frac{2.\frac{y}{x+1}}{1-\frac{y^2}{(x+1)^2}}$

sau khi giản ước cho cho $y(y\ne 0)$ và rút gọn ta được; $x^2-\frac{y^2}{3}=1$. Đường cong là hypebôn.

154. Tâm sai của hypebôn bằng $\sqrt{2}$. Lập phương trình đơn giản nhất của hypebôn đi qua điểm $M(\sqrt{3};\sqrt{2})$.

Giải. Theo định nghĩa tâm sai ta có thể viết $\frac{c}{a}=\sqrt{2}$ hay $c^2=2a^2$. Nhưng $c^2=a^2+b^2$ nên $a^2+b^2=2a^2$ hay $a^2=b^2$, nghĩa là hypebôn đều.

 Ta có đẳng thức khác từ điều kiện là điểm $M$ nằm trên hypebôn, nghĩa là $\frac{(\sqrt{3})^2}{a^2}-\frac{(\sqrt{2})^2}{b^2}=1$ hay $\frac{3}{a^2}-\frac{2}{b^2}=1$.

Vì $a^2=b^2$, nên ta được: $\frac{3}{a^2}-\frac{2}{a^2}=1$ nghĩa là $a^2=1$.

Vì vậy hypebôn cần tìm có dạng $x^2-y^2=1$.

155. Lập phương trình hypebôn đi qua điểm $M(9;8)$ và các tiệm cận của nó có phương trình $y=\pm \frac{2\sqrt{2}}{3}x$.

156. Tìm phương trình hypebôn có các đỉnh và các tiêu điểm nằm tại các tiêu điểm và các đỉnh tương ứng của êlip $\frac{x^2}{8}+\frac{y^2}{5}=1$.

157. Vẽ đường thẳng đi qua điểm $M(0;-1)$ và đỉnh phải của hypebôn $3x^2-4y^2=12$. Tìm giao điểm thứ hai của đường thẳng với hypebôn.

158. Cho hypebôn $x^2-y^2=8$. Tìm êlip đồng tiêu đi qua điểm $M(4;6)$.

159. Cho êlip $9x^2+25y^2=1$. Viết phương trình hypebôn đều đồng tiêu.

160. Góc giữa các tiệm cận của hypebôn bằng $60^0$. Tính tâm sai của hypebôn.

161. Trên nhánh trái của hypebôn $\frac{x^2}{64}-\frac{y^2}{36}=1$. Tìm điểm có vector bán kính tiêu phải bằng $18$.

162. Lập phương trình hypebôn nếu tâm sai của nó bằng $2$ và các tiêu điểm trùng với các tiêu điểm của êlip $\frac{x^2}{25}+\frac{y^2}{9}=1$.

163. Tìm các vector bán kính tiêu của hypebôn $\frac{x^2}{16}-\frac{y^2}{9}=1$ tại các giao điểm của nó với đường tròn $x^2+y^2=91$.

164. Chứng minh rằng độ dài của đường thẳng góc hạ từ tiêu điểm đến một trong hai tiệm cận của hypebôn bằng nửa trục ảo.

165. Chứng minh rằng tích các khoảng cách từ điểm bất kỳ của hypebôn $x^2-y^2=1$ đến các tiệm cận của nó là một hằng số.

166. Tìm phương trình quỹ tích các điểm cách đều đường tròn $x^2+4x+y^2=0$ và điểm $M(2;0)$.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 08-02-2019 - 07:22

[tritanngo99]

4. Parabôn.

Parabôn là quỹ tích các điểm cách đều một điểm cho trước( gọi là tiêu điểm) và một đường thẳng cho trước (gọi là đường chuẩn). Nếu đường chuẩn của parabôn là đường thẳng $x=\frac{-p}{2}$ với tiêu điểm là điểm $F(\frac{p}{2};0)$ thì phương trình parabôn có dạng $y^2=2px(1)$

Parabôn này đối xứng qua trục hoành (h.12, ở đó $p>0$).

Phương trình: $x^2=2py(2)$ là phương trình đối xứng qua trục tung. Với $p>0$ các parabôn $(1)$ và $(2)$ hướng về phía dương của các trục tương ứng, còn với $p<0$ thì hướng về phía âm.

  Độ dài vector bán kính tiêu của parabôn được xác định theo công thức $r=x+\frac{p}{2}(p>0).$

Các ví dụ:

167. Lập phương trình parabôn đối xứng qua trục $Ox$ có đỉnh tại gốc tọa độ, nếu độ dài của dây cung nào đó của parabôn này thẳng góc với trục $Ox$ bằng $16$ và khoảng cách từ dây cung đó đến đỉnh bằng $6$.

Giải. Vì biết độ dài của dây cung và khoảng cách từ nó đến đỉnh cũng biết các tọa độ của đầu mút $M$ của dây cung này trên parabôn. Phương trình parabôn có dạng $y^2=2px$; thay trong đó $x=6,y=8$ ta được: $8^2=2p.6$, suy ra $2p=\frac{32}{3}$.

Vì vậy phương trình parabôn cần tìm là $y^2=\frac{32}{3}$x.

168. Lập phương trình parabôn có đỉnh tại gốc tọa độ, đối xứng qua trục $Oy$ và chắn trên đường phân giác của các góc tọa độ thứ nhất và thứ ba một dây cung độ dài là $8\sqrt{2}$.

Giải. Phương trình parabôn cần tìm là $x^2=2py$, phương trình đường phân giác là $y=x$. Do đó các giao điểm của parabôn với đường phân giác là $O(0;0)$ và $m(2p;2p)$.

  Độ dài dây cung được xác định như khoảng cách giữa hai điểm $8\sqrt{2}=\sqrt{4p^2+4p^2}$, suy ra $2p=8$. Do đó phương trình parabôn cần tìm có dạng: $x^2=8y$.

169. Lập phương trình đơn giản nhất của parabôn, biết rằng tiêu điểm của nó nằm tại giao điểm của đường bằng $4x-3y-4=0$ với trục $Ox$.

170. Trên parabôn $y^2=8x$ tìm điểm có khoảng cách đến đường chuẩn của parabôn bằng $4$.

171. Lập phương trình parabôn có đỉnh tại gốc tọa độ, đối xứng qua trục $Ox$ và chắn trên đường thẳng $y=x$ dây cung có độ dài $4\sqrt{2}$.

172. Parabôn $y^2=2x$ chắn trên đường thẳng đi qua gốc tọa độ một dây cung bằng $\frac{3}{4}$. Lập phương trình đường thẳng này.

173. Lập phương trình đơn giản nhất của parabôn, nếu dây cung thẳng góc với trục đối xứng và chia đôi khoảng cách giữa tiêu điểm và đỉnh có độ dài bằng $1$.

174. Tìm điểm trên parabôn $y^2=32x$ mà khoảng cách từ nó đến đường thẳng $4x+3y+10=0$ bằng $2$.

175. Lập phương trình parabôn có đỉnh tại gốc tọa độ, đối xứng qua trục $Ox$ và đi qua điểm $M(4;2)$; xác định góc $\alpha$ giữa vector bán kính tiêu của điểm này và trục $Ox$.

 

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 08-02-2019 - 18:42

[tritanngo99]

PHẦN 4: CÁC PHÉP BIẾN ĐỔI TỌA ĐỘ VÀ SỰ RÚT GỌN PHƯƠNG TRÌNH CÁC ĐƯỜNG BẬC HAI.
1. Phép biến đổi tọa độ.

  Khi chuyển từ hệ tọa độ $xOy$ đến hệ mới $x'Oy'$( hướng của các trục tọa độ vẫn như cũ, điểm $O_1(a,b)$ được lấy làm gốc tọa độ mới; h.13); liên hệ giữa các tọa độ cũ và mới của điểm $M$ nào đó của mặt phẳng được xác định bằng công thức sau đây : $\left\{\begin{array}{I} x=x'+a,y=y'+b(1)\\ x'=x-a,y'=y-b(2)\end{array}\right.$

  Cặp công thức $(1)$ cho cách biểu diễn các tọa độ cũ qua các tọa độ mới, cặp công thức $(2)$ cho cách biểu diễn các tọa độ mới qua tọa độ cũ.

  Khi quay các trục tọa độ một góc $\alpha$ (gốc tọa độ vẫn như cũ, góc $\alpha$ được tính ngược chiều kim đồng hồ ; hình 14) sự phụ thuộc giữa các tọa độ cũ $(x;y)$ và $(x';y')$ được xác định bằng các công thức sau: $\left\{\begin{array}{I} x=x'cos \alpha-y'sin \alpha,y=x'sin \alpha+y'cos \alpha(3)\\ x'=xcos \alpha+ysin \alpha,y'=-xsin \alpha+ycos \alpha(4)\end{array}\right.$

Hình 13+14.

Các ví dụ:

176. Thực hiện phép tịnh tiến song song các trục tọa độ, trong đó gốc mới đặt tại điểm $O_1(3;-4)$. Biết các tọa độ cũ của điểm $M(7;8)$. Xác định các tọa độ mới của điểm này.

Giải. Ở đây $a=3,b=-4,x=7,y=8$. Theo công thức $(2)$ ta có: $x'=7-3=4,y'=8-(-4)=12$.

177. Cho điểm $M(4;3)$ trên mặt phẳng $xOy$. Quay hệ tọa độ quanh điểm gốc sao cho trục mới $Ox'$ đi qua $M$. Xác định các tọa độ cũ của điểm $A$ nếu biết các tọa độ mới của nó là $x'=5,y'=5$.

Giải. Vì $|OM|=\sqrt{4^2+3^2}=5$ nên $sin \alpha=\frac{3}{5},cos \alpha=\frac{4}{5}$; các công thức biến đổi tọa độ $(3)$ của bài toán này có dạng $x=\frac{4}{5}x'-\frac{3}{5}y';y=\frac{3}{5}x'+\frac{4}{5}y'$.

Cho $x'=y'=5$ ta được $x=1,y=7$.

178. Quay hệ tọa độ một góc $\alpha=\frac{\pi}{6}$. Xác định các tọa độ mới của điểm $M(\sqrt{3};3)$.

Giải. Sử dụng công thức $(4)$ ta được: 

$x'=\sqrt{3}cos \frac{\pi}{6}+3sin \frac{\pi}{6}=\frac{3}{2}+\frac{3}{2}=3$.

$y'=-\sqrt{3}sin \frac{\pi}{6}+3cos \frac{\pi}{6}=\frac{-\sqrt{3}}{2}+\frac{3\sqrt{3}}{2}=\sqrt{3}$.

179. Cho điểm $M(\frac{9}{2};\frac{11}{2})$. Để làm các trục tọa độ mới ta lấy các đường thẳng $2x-1=0$ (trục $O_1y'$), $2y-5=0$ (trục $O_1x'$). Tìm các tọa độ của điểm $M$ trong hệ tọa độ mới.

180. Cho điểm $M(4\sqrt{5};2\sqrt{5})$. Ta lấy đường thẳng $y=2x$ làm trục hoành độ mới và đường thẳng $y=\frac{-1}{2}x$ làm trục tung độ mới; khi đó các trục tọa độ mới tạo với các trục tọa độ cũ tương ứng những góc nhọn. Tìm các tọa độ của điểm $M$ trong hệ mới.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 09-02-2019 - 06:55

[tritanngo99]

2. Parabôn $y=Ax^2+Bx+C$ và hypebôn $y=\frac{kx+l}{px+q}$.

 Phương trình dạng $y=Ax^2+Bx+C$ được biến đổi thành dạng chính tắc của phương trình parabôn nhờ phép tịnh tiến song song các trục tọa độ, nghĩa là theo công thức $x=x'+a,y=y'+b$ ($a$ và $b$ là các tọa độ của điểm gốc mới, $x'$ và $y'$ là các tọa độ mới).

  Parabôn được xác định bởi phương trình $Ax^2+Bx+C$ có trục đối xứng song song với trục $Oy$ (tương tự, phương trình $x=Ay^2+By+C$ xác định parabôn có trục đối xứng song song với trục $Ox$).

  Hàm phân tuyến tính $y=\frac{kx+l}{px+q}$ xác định hypebôn đều nếu $kq-pl \ne 0,p\ne 0$; bằng phép tịnh tiến song song các trục tọa độ phương trình này biến đổi thành dạng chính tắc của phương trình hypebôn đều $xy=m$, nghĩa là thành phương trình hypebôn đều mà các trục tọa độ là các đường tiệm cận. Với $m>0$ các nhánh của hypebôn nằm trong các góc phần tư $I$ và $III$, còn với $m<0$ thì trong các góc phần tư $II$ và $IV$.

Các ví dụ: 

181. Đưa phương trình parabôn $y=9x^2-6x+2$ về dạng chính tắc.

Giải. Ta thay $x$ bằng $x'+a$ và $y$ bằng $y'+b$:

$y'+b=9(x'+a)^2-6(x'+a)+2,$ hay $y'=9x'^2+6x'(3a-1)+(9a^2-6a+2-b)$.

 Ta tìm $a$ và $b$ sao cho hệ số của $x'$ và số hạng tự do bằng không: $3a-1=0,9a^2-6a+2-b=0$, nghĩa là $a=\frac{1}{3},b=1$. Do đó phương trình chính tắc của parabôn là $x'^2=\frac{1}{9}y'$.

 Đỉnh của parabôn nằm tại điểm $O_1(\frac{1}{3};1)$ và $p=\frac{1}{18}$.

  Phương pháp khác để giải các bài toán thuộc loại này là: phương trình đã cho có dạng $y=Ax^2+Bx+C$( hay $x=Ay^2+By+C$) được đưa về dạng $(x-a)^2=2p(y-b)$ [tương ứng $(y-b)^2=2p(x-a)$]. Khi đó điểm $O_1(a;b)$ là đỉnh parabôn, dấu của tham số $p$ được xác định tùy theo parabôn hướng về phía nào - phía dương hay phía âm của các trục tương ứng $(Oy$ hay $Ox)$.

  Chẳng hạn viết phương trình $y=9x^2-6x+2$ dưới dạng $y=9(x^2-\frac{2}{3}x+\frac{1}{9})-1+2$ hay $y-1=9(x-\frac{1}{3})^2$, hay cuối cùng $(x-\frac{1}{3})^2=\frac{1}{9}(y-1)$.

  Từ đó ta lại thấy đỉnh parabôn nằm tại điểm $O_1(\frac{1}{3};1)$, tham số $p=\frac{1}{18}$ và các nhánh parabôn hướng về phía dương của trục $Oy$.

182. Đưa phương trình hypebôn $y=\frac{4x+5}{2x-1}$ về dạng $x'y'=k$. Tìm phương trình các tiệm cận của hypebôn đối với hệ tọa độ ban đầu.

Giải. Bằng phép tịnh tiến song song các trục tọa độ ta đưa phương trình đã cho về dạng: $(y'+b)(2x'+2a-1)=4x'+4a+5$.

hay $2x'y'+(2b-4)x'+(2a-1)y'=4a+b-2ab+5$.

Ta tìm $a$ và $b$ từ các điều kiện $2b-4=0$ và $2a-1=0$, nghĩa là $a=\frac{1}{2},b=2$. Khi đó phương trình hypebôn trong hệ tọa độ mới có dạng $x'y'=\frac{7}{2}$. Các tiệm cận của hypebôn là các trục tọa độ mới, vì vậy phương trình của chúng là $x'=\frac{1}{2},y'=2$.

  Phương pháp khác để giải các bài toán thuộc loại này là: phương trình dạng $y=\frac{kx+l}{px+q}$ được đưa về dạng $(x-a)(y-b)=m$; tâm hypebôn đặt tại điểm $O_1(a;b)$; các tiệm cận của nó là đường thẳng $x=a$ và $y=b$, dấu của $m$ được xác định như trước; tùy theo các nhánh của hypebôn nằm trong các góc nào giữa các tiệm cận.

  Chẳng hạn viết phương trình $y=\frac{4x+5}{2x-1}$ dưới dạng $2(x-\frac{1}{2})y-4(x-\frac{1}{2}+\frac{7}{4})=0$ hay $(2x-1)y-(4x+5)=0$, nghĩa là $2(x-\frac{1}{2})(y-2)=7$. Vì vậy phương trình hypebôn được đưa về dạng $(x-\frac{1}{2})(y-2)=\frac{7}{2}$; tâm hypebôn nằm tại điểm $O_1(\frac{1}{2};2)$, các nhánh của hypebôn nằm trong các góc phần tư $I$ và $III$ giữa các tiệm cận $x-\frac{1}{2}=0,y-2=0$ của nó.

183. Đưa phương trình các parabôn về dạng chính tắc:

a) $y=4x-2x^2$

b) $y=-x^2+2x+2$

c) $x=-4y^2+y$

d) $x=y^2+4y+5$.

184. Biến đổi phương trình các hypebôn về dạng $x'y'=m$

a) $y=\frac{2x}{4x-1}$

b) $y=\frac{2x+3}{3x-2}$

c) $y=\frac{10x+2}{5x+4}$

d) $y=\frac{4x+3}{2x+1}$.

 

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 09-02-2019 - 12:20

[tritanngo99]

3. Phương trình ngũ thức của đường bậc hai.

 Phương trình bậc hai dạng $Ax^2+Cy^2+2Dx+2Ey+F=0$

(không chứa số hạng $xy$, tích của các tọa độ) được gọi là phương trình ngũ thức của đường bậc hai. Nó xác định trên mặt phẳng $xOy$ êlip, hypebôn hay parabôn (kể cả các trường hợp suy biến của các đường này), với các trục đối xứng song song với các trục tọa độ, tùy theo dấu của tích các hệ số $A$ và $C$.

1. Nếu $AC>0$ thì phương trình này xác định êlip (thực, ảo hay suy biến thành một điểm); khi $A\equiv C$ thì êlip biến thành đường tròn.

2. Nếu $AC<0$ thì đường cong tương ứng là là hypebôn; nó có thể suy biến thành hai đường thẳng cắt nhau nếu vế trái của phương trình phân tích được thành tích hai nhân thức tuyến tính: $Ax^2+Cy^2+2Dx+2Ey+F=(a_1x+b_1y+c_1)(a_2x+b_2y+c_2)$.

3. Nếu $AC=0$ (nghĩa là $A=0,C\ne 0$ hoặc $C=0,A\ne 0$) thì phương trình xác định parabôn; nó có thể suy biến thành hai đường thẳng song song (thực, trùng nhau hay ảo) nếu vế trái của phương trình không chứa hoàn toàn hoặc $x$ hoặc $y$ (nghĩa là nếu phương trình có dạng $Ax^2+2Dx+F=0$ hoặc $Cy^2+2Ey+F=0$).

  Dạng của đường và vị trí của nó trên mặt phẳng dễ dàng nhận được bằng cách đưa phương trình về dạng $A(x-x_0)^2+C(y-y_0)^2=f$ (trong trường hợp $AC>0$ hay $AC<0$); từ phương trình nhận được ta cũng thấy rõ cả trường hợp suy biến của êlip và hypebôn.

  Trong trường hợp các đường không suy biến thì bằng cách chuyển gốc tọa độ đến điểm $O_1(x_0;y_0)$, phương trình nhận được của êlip hay hypebôn có thể đưa về dạng chính tắc.

  Trường hợp $AC=0$ đã được xét chi tiết trong mục trước, vì phương trình parabôn không suy biến ở đây có thể viết dưới dạng $y=a_1x^2+b_1x+c$ hay $x=a_1y^2+b_1y+c_1$.

185. Phương trình $4x^2+9y^2-8x-36y+4=0$ xác định đường gì?

Giải. Ta biến đổi phương trình đã cho như sau: $4(x^2-2x)+9(y^2-4y)=-4$;

$4(x^2-2x+1-1)+9(y^2-4y+4-4)=-4\iff 4(x-1)^2+9(y-2)^2=36$.

 Ta thực hiện phép tịnh tiến song song các trục tọa độ và lấy điểm $O'(1;2)$ làm gốc tọa độ mới.

  Sử dụng các công thức biến đổi tọa độ : $x=x'+1,y=y'+2$,

phương trình của đường đối với các trục mới có dạng $4x'^2+9y'^2=36$, hoặc $\frac{x'^2}{4}+\frac{y'^2}{9}=1$. Vì vậy đường đã cho là êlip.

186. Phương trình $x^2-9y^2+2x+36y-44=0$ xác định đường gì?

Giải. Biến đổi phương trình đã cho như sau: 

$(x^2+2x+1-1)-9(y^2-4y+4-4)=44\iff (x+1)^2-9(y-2)^2=44+1-36\iff (x+1)^2-9(y-2)^2=9$.

 Ta thực hiện phép tịnh tiến song song các trục tọa độ và lấy điểm $O'(-1;2)$ làm gốc tọa độ. Các công thức biến đổi tọa độ: $x=x'-1,y=y'+2$.

Sau phép biến đổi tọa độ phương trình có dạng: $x'^2-9y'^2=9$ hay $\frac{x'^2}{9}-y'^2=1$.

  Đường này là hypebôn. Các tiệm cận của hypebôn này đối với các trục mới là các đường thẳng $y'=\pm \frac{1}{3}x'$.

 Các phương trình dưới đây xác định những đường gì?

187. $36x^2+36y^2-36x-24y-23=0$.

188. $16x^2+25y^2-32x+50y-359=0$.

189. $\frac{1}{4}x^2-\frac{1}{9}y^2-x+\frac{2}{3}y-1=0$

190. $x^2+4y^2-4x-8y+8=0$.

191. $x^2+4y^2+8y+5=0$.

192. $x^2-y^2-6x+10=0$.

193. $2x^2-4x+2y-3=0$.

194. $x^2-6x+8=0$.

195. $x^2+2x+5=0$.

[tritanngo99]

4.Đưa phương trình tổng quát của đường bậc hai về dạng chính tắc.

 Nếu đường bậc hai cho bởi phương trình : $Ax^2+2Bxy+Cy^2+2Dx+2Ey+F=0$.

 thì bằng cách áp dụng phép quay các trục tọa độ theo công thức $x=x'cos \alpha-y'sin \alpha,y=x'sin \alpha+y'cos \alpha$, với cách chọn $\alpha$ thích hợp ta bỏ được trong phương trình số hạng chứa tích các tọa độ.

  Các phép tính biến đổi tiếp theo đã được xét trong phần trên.

Trường hợp suy biến của đường bậc hai thành hai đường thẳng có thể dễ dàng nhận thấy từ phương trình xuất phát bằng cách say đây: xem phương trình đã cho như phương trình bậc hai đối với $y$ (giả sử rằng hệ số của $y^2$ khác không), ta giải nó đối với $y$; nếu khi đó dưới dấu căn là bình phương của nhị thức $ax+b$ nào đấy; thì căn này khai phương được và $y$ có hai giá trị $y_1=k_1x+b_1;y_2=k_2x+b_2$. Điều đó cũng chứng tỏ rằng, đường cong suy biến thành hai đường thẳng. Cũng có thể giải phương trình đã cho đối với $x$. Nếu trong phương trình tổng quát của đường bậc hai $A=C=0$ (dĩ nhiên $B\ne 0$) thì phương trình đã cho xác định cặp đường thẳng khi và chỉ khi $\frac{B}{D}=\frac{2E}{F}$. Trong trường hợp này vế trái của phương trình phân tích được thành các nhân thức bậc nhất.

Các ví dụ:

196. Chứng minh rằng phương trình $9x^2+24xy+16y^2-25=0$ xác định một cặp đường thẳng.

Giải. Ta viết lại phương trình dưới dạng $(3x+4y)^2-25=0$. Phân tích vế trái thành nhân thức ta được: $(3x+4y+5)(3x+4y-5)=0$

 Vì vậy phương trình đã cho xác định các đường thẳng: $3x+4y+5=0$ và $3x+4y-5=0$.

197. Chứng minh rằng phương trình $3x^2+8xy-3y^2-14x-2y+8=0$ xác định một cặp đường thẳng.

Giải. Ta viết lại phương trình dưới dạng: $3y^2-2(4x-1)y-(3x^2-14x+8)=0$.

Giải phương trình đối với $y: y=\frac{4x-1\pm \sqrt{(4x-1)^2+(9x^2-42x+24)}}{3}$

hay $y=\frac{4x-1\pm (5x-5)}{3}$.

Ta được phương trình các đường thẳng $y=3x-2$ và $y=\frac{-x+4}{3}$. Các phương trình này có thể viết dưới dạng $3x-y-2=0$, $x+3y-4=0$.

198. Phương trình $xy+2x-4y-8=0$ xác định đường gì?

Giải. Ta viết phương trình dưới dạng $x(y+2)-4(y+2)=0$ hay $(x-4)(y+2)=0$. Vì vậy phương trình xác định hai đường thẳng $x-4=0$ và $y+2=0$, một đường song song với trục $Ox$ còn đường còn lại song song với trục $Oy$.

199. Đưa về dạng chính tắc phương trình: $5x^2+4xy+8y^2+8x+14y+5=0$.

Giải. 

1) Ta biến đổi phương trình này bằng cách áp dụng các công thức quay trục tọa độ $(3)$. Ta có:

$5(x'cos \alpha-y'sin \alpha)^2+4(x'cos \alpha-y'sin \alpha)(x'sin \alpha+y'cos \alpha)+8(x'sin \alpha+y'cos \alpha)^2+8(x'cos \alpha-y'sin \alpha)+14(x'sin \alpha+y'cos \alpha)+5=0$.

  Ta tìm $\alpha$ từ điều kiện $4(cos^2 \alpha-sin^2\alpha)+6sin \alpha cos \alpha=0$;

nghĩa là cho hệ số của $x'y'$ bằng $0$. Ta được phương trình $2tan^2 \alpha-3tan \alpha-2=0$. Từ đó $tan \alpha_1=2,tan \alpha_2=-\frac{1}{2}$.

  Chú ý rằng các giá trị này của $tan \alpha$ tương ứng với hướng trực giao nhau. Vì vậy nếu chọn $tan \alpha= -\frac{1}{2}$ thay cho $tan \alpha=2$, ta chỉ thay đổi vai trò của các trục $x'$ và $y'$ (h.15).

Giả sử $tan \alpha=2$, khi đó $sin \alpha=\pm \frac{2}{\sqrt{5}}, cos \alpha=\pm \frac{1}{\sqrt{5}}$, ta lấy giá trị dương của $sin \alpha$ và $cos \alpha$. Khi đó phương trình có dạng: $9x'^2+4y'^2+\frac{36}{\sqrt{5}}x'-\frac{2}{\sqrt{5}}y'+5=0$.

hay $9(x'^2+\frac{4}{\sqrt{5}}x')+4(y'^2-\frac{1}{2\sqrt{5}}y')=-5$.

2) Ta bổ sung các biểu thức trong ngoặc thành các chính phương: 

$9(x'+\frac{2}{\sqrt{5}})^2+4(y'-\frac{1}{4\sqrt{5}})^2=\frac{36}{5}+\frac{1}{20}-5$

hay $9(x'+\frac{2}{\sqrt{5}})^2+4(y'-\frac{1}{4\sqrt{5}})^2=\frac{9}{4}$ hay $\frac{x'^2}{\frac{1}{4}}+\frac{y'^2}{\frac{9}{16}}=1$ (phương trình êlip).

200. Đưa phương trình $6xy+8y^2-12x-26y+11=0$ về dạng chính tắc.

Giải.

1) Ta biến đổi phương trình này bằng cách ứng dụng các công thức quay trục tọa độ $(3)$. Ta có:

$6(x'cos \alpha-y'sin \alpha)(x'sin \alpha+y'cos \alpha)+8(x'sin \alpha+y'cos \alpha)^2-12(x'cos \alpha-y'sin \alpha)-26(x'sin \alpha+y'cos \alpha)+11=0$

hay $(6sin \alpha cos\alpha+8sin^2 \alpha)x'^2+(8cos^2\alpha-6sin \alpha cos \alpha)y'^2+[16sin \alpha cos \alpha+6(cos^2 \alpha-sin^2 \alpha)]x'y'-(12cos \alpha+26sin \alpha)x'-(26cos \alpha-12sin \alpha)y'+11=0$.

 Cho hệ số của $x'y'$ bằng không, ta có: $16sin \alpha cos \alpha+6(cos^2 \alpha-sin^2\alpha)=0$ hay $3tan^2\alpha-8\alpha-3=0$. Do đó $tan\alpha_1=3,tan\alpha_2=-\frac{1}{3}$; ta chọn $tan\alpha=3$, khi đó $sin \alpha=\pm \frac{3}{\sqrt{10}},cos \alpha=\pm \frac{1}{\sqrt{10}}$. Ta lấy giá trị dương của $sin \alpha$ và $cos \alpha$. Khi đó phương trình có dạng: $9x'^2-y'^2-9\sqrt{10}x'+\sqrt{10}y'+11=0$,

hay $9(x'^2-\sqrt{10}x')-(y'^2-\sqrt{10}y')=-11$.

2) Ta bổ sung các biểu thức trong ngoặc thành các chính phương: $9(x'-\frac{\sqrt{10}}{2})^2-(y'-\frac{\sqrt{10}}{2})^2=\frac{45}{2}-\frac{5}{2}-11$

hay $9(x'-\frac{\sqrt{10}}{2})^2-(y'-\frac{\sqrt{10}}{2})^2=9$.

 Lấy điểm $O'(\frac{\sqrt{10}}{2};\frac{\sqrt{10}}{2})$ làm điểm gốc mới và áp dụng các công thức biến đổi tọa độ $x'=x''+\frac{\sqrt{10}}{2},y'=y''+\frac{\sqrt{10}}{2}$

ta được: $9x''^2-y''^2=9$ hay $x''^2-\frac{y''^2}{9}=1$ (phương trình hypebôn).

201. Đưa phương trình $x^2-2xy+y^2-10x-6y+25=0$ về dạng chính tắc.

Giải. 

1) Ta biến đổi phương trình nhờ phép quay các trục:

$(x'cos \alpha-y'sin \alpha)^2-2(x'cos \alpha-y'sin \alpha)(x'sin \alpha+y'cos \alpha)+(x'sin \alpha+y'cos \alpha)^2-10(x'cos \alpha-y'sin \alpha)-6(x'sin \alpha+y'cos \alpha)+25=0$ 

hay $(cos^2\alpha-2sin \alpha cos\alpha)x'^2+(sin^2\alpha+2sin \alpha cos \alpha+cos^2\alpha)y'^2+2(sin^2\alpha-cos^2\alpha)x'y'-(10cos\alpha+6sin \alpha)x'+(10sin \alpha-6cos \alpha)y'+25=0$.

 Cho hệ số của tích $x'y'$ bằng không, ta có: $2(sin^2\alpha-cos^2\alpha)=0$, từ đó $tan^2\alpha=1$, tức là$tan\alpha_1=1,tan\alpha_2=-1$. Ta lấy $tan \alpha=1$, khi đó $\alpha=\frac{\pi}{4}$ và $sin \alpha=\frac{\sqrt{2}}{2},cos\alpha=\frac{\sqrt{2}}{2}$; phương trình có dạng: $2y'^2-8\sqrt{2}x'+2\sqrt{2}y'+25=0$ hay $2(y'^2+\sqrt{2}y')-8\sqrt{2}x'+25=0$.

2) Ta bổ sung biểu thức trong ngoặc thành chính phương: $2(y'+\frac{\sqrt{2}}{2})^2=8\sqrt{2}x'-24$

hay $(y'+\frac{\sqrt{2}}{2})^2=4\sqrt{2}(x'-\frac{3}{\sqrt{2}})$.

 Chọn điểm $O(\frac{3}{\sqrt{2}};-\frac{\sqrt{2}}{2})$ làm gốc mới và áp dụng các công thức biến đổi tọa độ $x'=x''+\frac{3}{\sqrt{2}},y'=y''-\frac{\sqrt{2}}{2}$.

ta được: $y''^2=4\sqrt{2}x''$ (phương trình parabôn).

  Chứng minh rằng các phương trình dưới đây xác định các đường cong suy biến thành cặp đường thẳng và tìm phương trình các đường thẳng đó:

202. $25x^2+10xy+y^2-1=0$.

203. $x^2+2xy+y^2+2x+2y+1=0$.

204. $8x^2-18xy+9y^2+2x-1=0$.

 Đưa phương trình các đường cong sau đây về dạng chính tắc:

205. $14x^2+24xy+21y^2-4x+18y-139=0$.

206. $4xy+3y^2+16x+12y-36=0$.

207. $9x^2-24xy+16y^2-20x+110y-50=0$.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 10-02-2019 - 04:27

[tritanngo99]

Phần 5: ĐỊNH THỨC CẤP HAI, CẤP BA. CÁC HỆ PHƯƠNG TRÌNH TUYẾN TÍNH HAI VÀ BA ẨN.

1. Định thức cấp hai và hệ phương trình tuyến tính. Định thức cấp hai tương ứng với bảng các phần tử $\begin{align*}\begin{pmatrix} a_1 & b_1\\ a_2 & b_2 \end{pmatrix}\end{align*}$ được xác định bởi đẳng thức: $\begin{align*}\begin{vmatrix} a_1 &b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}=a_1b_2-a_2b_1$.

  Hệ phương trình tuyến tính hai ẩn $\left\{\begin{array}{I} a_1x+b_1y=c_1\\ a_2x+b_2y=c_2\end{array}\right.$ có nghiệm duy nhất, nếu định thức của nó $D=\begin{align*}\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}\ne 0$ và nghiệm được xác định theo công thức: $x=\frac{D_x}{D}=\frac{\begin{align*}\begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \end{vmatrix}\end{align*}}{\begin{align*}\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}};y=\frac{D_y}{D}=\frac{\begin{align*}\begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}\end{align*}}{\begin{align*}\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}}(1)$. (công thức Crame).

  Nếu định thức $D=0$, thì hoặc hệ không tương thích (khi $D_x=\begin{align*}\begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \end{vmatrix}\end{align*}\ne 0$ và $\begin{align*}\begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}\end{align*}\ne 0$), hoặc vô định (khi $D_x=D_y=0$). Trong trường hợp cuối cùng hệ được đưa về một phương trình (chẳng hạn phương trình đầu), còn phương trình thứ hai là hệ quả của phương trình đầu.

  Điều kiện không tương thích của hệ có thể cho dưới dạng $\frac{a_1}{a_2}=\frac{b_1}{b_2}\ne \frac{c_1}{c_2}$, còn điều kiện vô định có dạng $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$.

  Phương trình tuyến tính gọi là thuần nhất nếu số hạng tự do của phương trình này bằng không.

 Ta xét hệ hai phương trình thuần nhất ba ẩn:

$\left\{\begin{array}{I} a_1x+b_1y+c_1z=0\\ a_2x+b_2y+c_2z=0\end{array}\right.$

1) Nếu $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$ thì hệ đưa đến một phương trình( chẳng hạn phương trình đầu), từ phương trình này một trong các ẩn được biểu diễn qua hai ẩn kia, mà giá trị của chúng là tùy ý.

2) Nếu điều kiện $\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$ không thỏa mãn, thì nghiệm của hệ tìm được theo công thức

$x=\begin{align*}\begin{vmatrix} b_1 & c_1 \\ b_2 & c_2 \end{vmatrix}\end{align*}.t$; $y=-\begin{align*}\begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}\end{align*}.t$;$z=\begin{align*}\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}.t(2)$

trong đó $t$ có thể nhận giá trị tùy ý. Nghiệm này cũng có thể viết dưới dạng tỷ lệ: $\frac{x}{\begin{align*}\begin{vmatrix} b_1 & c_1 \\ b_2 & c_2 \end{vmatrix}\end{align*}}=\frac{y}{\begin{align*}\begin{vmatrix} c_1 & a_1 \\ c_2 & a_2 \end{vmatrix}\end{align*}}=\frac{z}{\begin{align*}\begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}\end{align*}}=t$.

  Nhưng với cách viết này của nghiệm ta phải nhớ rằng, nếu một trong các mẫu số bằng $0$ thì tử số tương ứng cũng phải bằng $0$.

Các ví dụ: 

208. Giải hệ phương trình:

$\left\{\begin{array} (a+b)x-(a-b)y=4ab \\ (a-b)x+(a+b)y=2(a^2-b^2)\end{array}\right.$

Giải. Ta tìm định thức $D$ của hệ và các định thức $D_x,D_y$ ở các tử số trong công thức $(1)$.

$D=\begin{align*}\begin{vmatrix} a+b & -(a-b) \\ a-b & a+b \end{vmatrix}\end{align*}=(a+b)^2+(a-b)^2=2(a^2+b^2)$.

$D_x=\begin{align*}\begin{vmatrix} 4ab & -(a-b) \\ 2(a^2-b^2) & a+b \end{vmatrix}\end{align*}=4a^2b+4ab^2+2a^3-2a^2b-2ab^2+2b^3=2(a^2+b^2)(a+b)$.

$D_y=\begin{align*}\begin{vmatrix} a+b & 4ab \\ a-b & 2(a^2-b^2) \end{vmatrix}\end{align*}=2a^3+2a^2b-2ab^2-2b^3-4a^2b+4ab^2=2(a^3-a^2b+ab^2-b^3)=2(a^2+b^2)(a-b)$.

Từ đó $x=\frac{D_x}{D}=a+b,y=\frac{D_y}{D}=a-b$.

209. Giải hệ phương trình tuyến tính thuần nhất.

$\left\{\begin{array}{I} 3x+4y+5z=0\\ x+2y-3z=0\end{array}\right.$

Giải. Áp dụng công thức $(2)$ ta được: 

$x=\begin{align*}\begin{vmatrix} 4 & 5 \\ 2 & -3 \end{vmatrix}\end{align*}.t=-22t$, $y=-\begin{align*}\begin{vmatrix} 3 & 5 \\ 1 & -3 \end{vmatrix}\end{align*}.t=14t$, $z=\begin{align*}\begin{vmatrix} 3 & 4 \\ 1 & 2 \end{vmatrix}\end{align*}.t=2t$, trong đó $t$ có thể lấy giá trị tùy ý.

Giải các hệ phương trình

210. $\left\{\begin{array}{I} 5x-3y=1\\ x+11y=6 \end{array}\right.$

211.  $\left\{\begin{array}{I} 2x+y=\frac{1}{5}\\ 4x+2y=\frac{1}{3} \end{array}\right.$

212.  $\left\{\begin{array}{I} ax-by=a^2+b^2\\ bx+ay=a^2+b^2 \end{array}\right.$

213.  $\left\{\begin{array}{I} 3x+2y=\frac{1}{6}\\ 9x+6y=\frac{1}{2} \end{array}\right.$

214. $\left\{\begin{array}{I} x-2y+z=0\\ 3x-5y+2z=0 \end{array}\right.$

215.  $\left\{\begin{array}{I} xcos \alpha-ysin \alpha=cos 2\alpha\\ xsin \alpha+y cos \alpha=sin 2\alpha \end{array}\right.$

216.  $\left\{\begin{array}{I} a^2x-2(a^2+b^2)y+b^2z=0\\ 2x+2y-3z=0 \end{array}\right.$

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 10-02-2019 - 05:28