Chủ đề này có 1 trả lời

[toanND]

Cho hai đường tròn $(\omega _{1})$ và $(\omega _{2})$ cắt nhau tại hai điểm A và B. Một đường thẳng qua B cắt $(\omega _{1})$ và $(\omega _{2})$ tại C và D. Một đường thẳng khác qua B cắt $(\omega _{1})$, $(\omega _{2})$ tại P, Q. Chứng minh rằng nếu CD = EF thì C, F, M, N đồng viên với M, N lần lượt là điểm chính giữa các cung nhỏ BP và BQ.

[tritanngo99]

Cho hai đường tròn $(\omega _{1})$ và $(\omega _{2})$ cắt nhau tại hai điểm A và B. Một đường thẳng qua B cắt $(\omega _{1})$ và $(\omega _{2})$ tại C và D. Một đường thẳng khác qua B cắt $(\omega _{1})$, $(\omega _{2})$ tại P, Q. Chứng minh rằng nếu CD = EF thì C, F, M, N đồng viên với M, N lần lượt là điểm chính giữa các cung nhỏ BP và BQ.

Đầu tiên mình xin đính chính lại đề một chút:

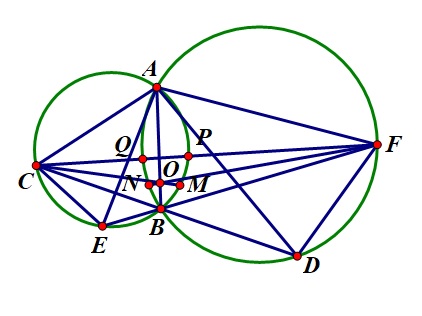
Đề bài: Cho hai đường tròn $(\omega_1)$ và $(\omega_2)$ cắt nhau tại hai điểm $A$ và $B$. Một đường thẳng qua $B$ cắt $(\omega_1)$ và $(\omega_2)$ lần lượt tại $C$ và $D$. Một đường thẳng khác qua $B$ cắt $(\omega_1)$ và $(\omega_2)$ lần lượt tại $E$ và $F$. Gọi $P,Q$ lần lượt là giao điểm của $CF$ với $(\omega_1)$ và $(\omega_2)$. Chứng minh rằng: Nếu $CD=EF$ thì $C,F,M,N$ đồng viên với $M,N$ lần lượt là điểm chính giữa các cung nhỏ $BP$ và $BQ$.

Lời giải:

1. Đầu tiên ta đi chứng minh: $\triangle{ACD}=\triangle{AEF}$.

Thật vậy: Ta dễ dàng chứng minh được: $\angle{ACD}=\angle{ACB}=\angle{AEB}=\angle{AEF}$ và $\angle{ADC}=\angle{ADB}=\angle{AFB}=\angle{AFE}$.

Và kết hợp với giải thiết $EF=CD$ ta suy ra được: $\triangle{ACD}=\triangle{AEF}(g.c.g)$.

Khi đó ta suy ra được: $AC=AE$ và $AF=AD$.

2. Tiếp theo ta đi chứng minh: $BA$ là tia phân giác $\angle{CBF}$.

Thật vậy: Do $AC=AE\implies \triangle{ACE}$ cân tại $A$ suy ra $\angle{ABC}=\angle{AEC}=\frac{180^0-\angle{CAE}}{2}\text{     (1)}$.

và tương tự: Do $AF=AD\implies \triangle{ADF}$ cân tại $A$ suy ra $\angle{ABF}=\angle{ADF}=\frac{180^0-\angle{DAF}}{2}\text{     (2)}$.

Mặt khác ta lại có: $\angle{CAE}=\angle{CBE}=\angle{DBF}=\angle{DAF}$.

Nên từ $(1)$ và $(2)$ suy ra $\angle{ABC}=\angle{ABF}$ hay $AB$ là tia phân giác góc $CBF$.

3. Chứng minh: Trong $\triangle{CBF}$: $BA,CM,FN$ đồng quy.

Thật vậy: Do $M,N$ lần lượt là điểm chính giữa của các cung nhỏ $BP,BQ$ nên suy ra $CM,FN$ lần lượt là tia phân giác các góc $\angle{BCF},\angle{BFC}$

Và kết hợp với $BA$ là tia phân giác góc $\angle{CBF}$ ta suy ra được $BA,CM,FN$ đồng quy.

4. Cuối cùng ta đi chứng minh $C,N,M,F$ đồng viên.

Thật vậy: Gọi $O$ là giao điểm của ba đường đồng quy $BA,CM,FN$. Khi đó ta có:

$+OA.OB=OM.OC$ (do $A,M,B,C$ đồng viên).

$+OA.OB=ON.OF$  (do $A,N,B,F$ đồng viên)

$\implies OM.OC=ON.OF$ hay bốn điếm $M,N,C,F$ đồng viên.

Vậy ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi tritanngo99: 02-02-2019 - 16:42