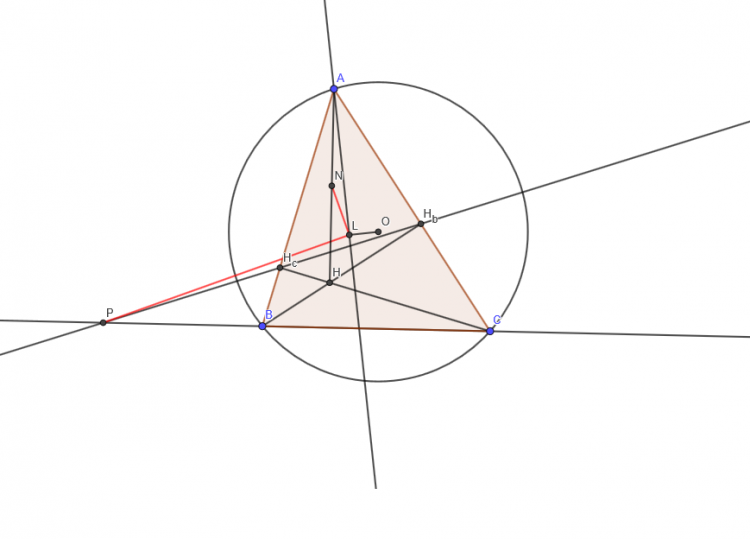
Gọi AQ là đường đối trung ứng với đỉnh A của tam giác ABC. AQ cắt (O) lần thứ hai tại T
$\Rightarrow$ Tứ giác ABTC điều hòa $\Rightarrow$ SA tiếp xúc với (O) tại A (S là giao của OL với BC).
Gọi $H_{a}$ là chân đường cao kẻ từ A của tam giác ABC. K là giao của OL với $AH_{a}$.
$\Rightarrow$ K là trực tâm tam giác AQS $\Rightarrow QK \perp AS$
Gọi M, I lần lượt là trung điểm của BC, $H_{b}H_{c}$. Khi đó M, I, N thẳng hàng và $MN\perp H_{b}H_{c}$
Mặt khác dễ thấy $AS \parallel H_bH_c$ $\Rightarrow QK \parallel MN$
$KLQH_a$ nội tiếp $\Rightarrow \widehat{H_aLQ}=\widehat{H_aKQ}=\widehat{H_aNI}(KQ\parallel MN)$
$\Rightarrow NILH_a$ nội tiếp. Mặt khác $I,H_a$ cùng nằm trên đường tròn đường kính NP
Suy ra L nằm trên đường tròn đường kính NP$\Rightarrow \widehat{NLP}=90^0$ (đpcm)