Chủ đề này có 2 trả lời

[KietLW9]

$\boxed{Problem 18}$Cho $\Delta ABC$ vuông tại $A$, đường phân giác $AD$ ($D$ thuộc $BC$). Qua $A$ vẽ đường thẳng $d$ vuông góc với $AD$. Từ $B,C$ vẽ đường thẳng vuông góc với $d$ cắt $d$ lần lượt tại $M,N$. Chứng minh rằng: $AD\leqslant \frac{MN}{2}$ 

Bài viết đã được chỉnh sửa nội dung bởi KietLW9: 21-04-2021 - 18:05

[DaiphongLT]

Gọi AC cắt MB tại K. Dễ thấy $AM=MB, AN=NC$
Ta có AD//BK $\Rightarrow \frac{AD}{BK}=\frac{AC}{KC}$$\Rightarrow AD=\frac{KB.AC}{KC}=\frac{KB.NC}{MN}$
Do đó bài toán cần cm $\frac{KB.NC}{MN}\leq \frac{MN}{2}\Rightarrow MN^2\geq 2.KB.NC=4.AM.AN$ (hn đúng)

[KietLW9]

My solution: 

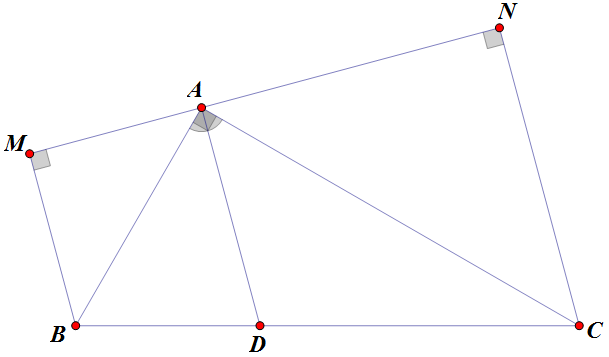
Từ $B$ và $C$ lần lượt hạ các đường vuông góc xuống $AD$ cắt $AD$ tại $B'$ và $C'$

Dễ có các tam giác $ABB'$ và $ACC'$ vuông cân nên $BB'=\frac{1}{\sqrt{2}}AB,CC'=\frac{1}{\sqrt{2}}AC$

Ta có: $S_{ABD}+S_{ACD}=S_{ABC}\Rightarrow \frac{1}{2}BB'.AD+\frac{1}{2}CC'.AD=\frac{1}{2}AB.AC\Rightarrow AD=\frac{AB.AC}{BB'+CC'}=\frac{\sqrt{2}AB.AC}{AB+AC}\leqslant \frac{\sqrt{2}.\frac{(AB+AC)^2}{4}}{AB+AC}=\frac{1}{2\sqrt{2}}(AB+AC)=\frac{1}{2\sqrt{2}}(\sqrt{2}BB'+\sqrt{2}CC')=\frac{BB'+CC'}{2}=\frac{MN}{2}(Q.E.D)$

Đẳng thức xảy ra khi $\Delta ABC$ vuông cân tại $A$.

Bài viết đã được chỉnh sửa nội dung bởi KietLW9: 22-04-2021 - 12:11