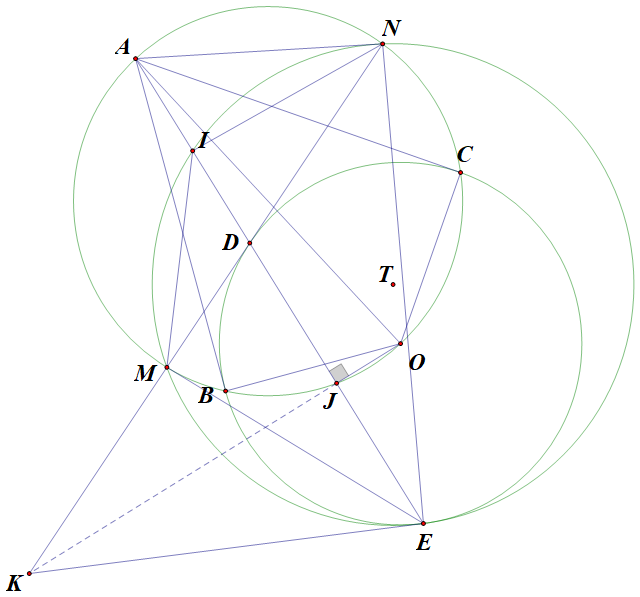
Chứng minh rằng IT luôn đi qua một điểm cố định
Bắt đầu bởi alexander123, 04-08-2021 - 09:31
#2
Đã gửi 04-08-2021 - 10:03
KietLW9
-
- Điều hành viên THCS
-
- 1737 Bài viết
Đại úy
a) Gọi $J$ là giao điểm của $AD$ với đường tròn ngoại tiếp tứ giác $ABOC$
Dễ thấy $AO$ là đường kính của đường tròn $(ABOC)$ nên $\widehat{AJO}=90^{\circ}$
Mà $\Delta ODE$ cân tại $O$ nên $J$ là trung điểm của DE
Từ đó ta có: $DM.DN=DA.DJ=2DI.\frac{1}{2}DE=DI.DE$
Do vậy bốn điểm $M,E,N,I$ cùng thuộc một đường tròn $(T)$
b) Kẻ tiếp tuyến với đường tròn $(O)$ tại $E$ thì $DE$ vuông góc với $KO$ mà $JO$ vuông góc $DE$ nên $K,O,J$ thẳng hàng
$\Delta KEO$ vuông tại E có $EJ$ là đường cao nên $EK^2=KJ.KO$
Mà dễ thấy $KJ.KO=KM.KN$ nên $EK^2=KM.KN$
Từ đó suy ra $KE$ là tiếp tuyến của $(T)$ suy ra $(O)$ và $(T)$ tiếp xúc nhau tại $E$
c) Từ câu b) ta dễ có: $\widehat{OED}=\widehat{ODE}=\widehat{TIE}$ nên $OD//IT$
Mà $I$ là trung điểm của $AD$ nên $IT$ đi qua trung điểm của $AO$ là điểm cố định (đpcm)
Trong cuộc sống không có gì là đẳng thức , tất cả đều là bất đẳng thức 
$\text{LOVE}(\text{KT}) S_a (b - c)^2 + S_b (c - a)^2 + S_c (a - b)^2 \geqslant 0\forall S_a,S_b,S_c\geqslant 0$
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh
