Chủ đề này có 3 trả lời

[phuc_90]

             ĐẠI HỌC QUỐC GIA TP.HCM                                            ĐỀ DỰ TUYỂN MÔN TOÁN NĂM 2021-2022

       TRƯỜNG PHỔ THÔNG NĂNG KHIẾU                                                  Ngày thi :   25/09/2021

----------------------------------------------------------                            Thời gian làm bài 180 phút, không kể thời gian phát đề

 

Bài 1. (5,0 điểm)

 

Cho các số thực dương $a,b,c$ thỏa $a^2+b^2+c^2=3$

 

a)   Chứng minh rằng    $a^{4n}+b^{4n}+c^{4n}+a^nb^n+b^nc^n+c^na^n\geq 6 \,\,\,,\,\,\forall n\in \mathbb{N}$

 

b)   Hỏi bất đẳng thức trên còn đúng khi thay $n=\frac{2}{3}$ ?

 

Bài 2. (5,0 điểm)

 

Cho $n$ là số nguyên dương chẵn, có tổng các ước nguyên dương của nó là số lẻ. Chứng minh rằng tổng các ước chính phương (nhỏ hơn $n$) của $n$ sẽ không nhỏ hơn $\frac{n}{4}$

 

Bài 3. (5,0 điểm)

 

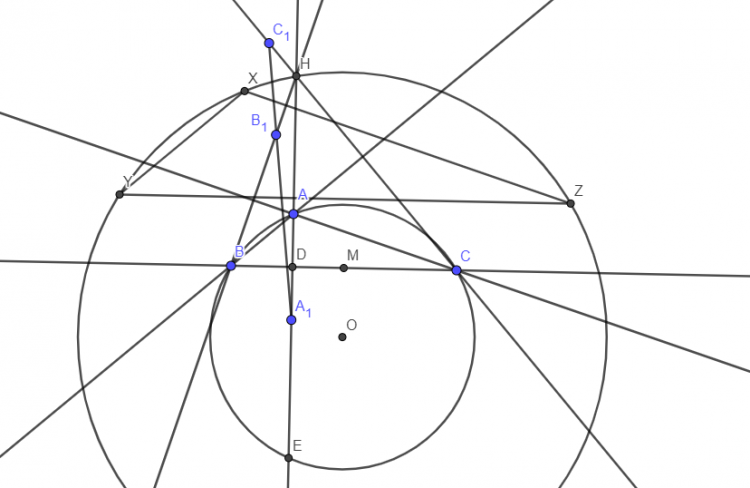
Cho tam giác $ABC$, gọi $A_1\,,\,B_1\,,\,C_1$ lần lượt là các điểm đối xứng của $A\,,\,B\,,\,C$ qua $BC\,,\,CA\,,\,AB$

Chứng minh rằng   $A_1\,,\,B_1\,,\,C_1$  thẳng hàng khi và chỉ khi  $cosA\,cosB\,cosC\,\,=\,\,-\frac{3}{8}$

 

Bài 4. (5,0 điểm)

 

Một quốc gia có $99$ thành phố, khoảng cách giữa hai thành phố bất kì không vượt quá $1000$ km. Hai thành phố thuộc quốc gia này được gọi là "xa nhau" nếu khoảng cách giữa chúng lớn hơn hoặc bằng $500\sqrt{2}$ km. Hỏi quốc gia này có bao nhiêu cặp thành phố xa nhau ?

 

                                                                ---------------------------  HẾT ---------------------------------

[LTBN]

Bài 1:

a) Với n = 0 thì bđt trở thành đẳng thức.

Với n = 1 ta cần chứng minh: $\sum a^4+\sum ab\geq 6\Leftrightarrow \sum ab-2\sum a^2b^2\geq -3$

$\Leftrightarrow q-2q^2+4rp\geq -3$. (Với $p=a+b+c;q=ab+bc+ca;r=abc$)

+) Nếu $0\leq q\leq \frac{3}{2}$ thì $q-2q^2+4rp\geq q-2q^2=(q+1)(3-2q)-3\geq -3$.

+) Nếu $3\geq q\geq \frac{3}{2}$ thì theo bđt Schur ta có $rp\geq \frac{p^2(4q-p^2)}{9}=\frac{(2q+3)(2q-3)}{9}$.

Do đó ta chỉ cần cm $q-2q^2+4\frac{(2q+3)(2q-3)}{9}\geq -3\Leftrightarrow (q-3)(2q-3)\leq 0$. (luôn đúng)

Với $n\geq 2$: Có $\sum a^{4n}+\sum a^nb^n\geq \frac{(a^4+b^4+c^4+ab+bc+ca)^n}{6^{n-1}}\geq 6$.

b) Với $n=\frac{2}{3}$ ta cho $a\to 0;b,c\to \sqrt{\frac{3}{2}}$ thì bđt không đúng.

[LTBN]

Bài 2. (5,0 điểm)

 

Cho $n$ là số nguyên dương chẵn, có tổng các ước nguyên dương của nó là số lẻ. Chứng minh rằng tổng các ước chính phương (nhỏ hơn $n$) của $n$ sẽ không nhỏ hơn $\frac{n}{4}$

Giả sử $n=2^a.p_1^{k_1}.p_2^{k_2}...p_x^{k_x}$ với $p_1,p_2,...,p_x$ là các số nguyên tố lẻ.

Theo công thức tính tổng các ước nguyên dương của n:

$\sigma(n)=\prod_{i=1}^{x}\frac{p_i^{k_i+1}-1}{p_i-1}.(2^{a+1}-1)$.

Do $\sigma(n)$ là lẻ nên $\frac{p_i^{k_i+1}-1}{p_i-1}$ là lẻ với mọi $i\in\overline{1,x}$.

Nếu tồn tại i sao cho $k_i$ là lẻ thì đặt $k_i=2m-1$. Ta có $\frac{p_i^{2m}-1}{p_i-1}=\frac{p_i^m-1}{p_i-1}.(p_i^m+1)$ là số chẵn. (vô lí)

Do đó $k_i$ là số chẵn $\forall i\in\overline{1,x}$.

Đặt $k_i=2h_i$ thì $n=2^a.p_1^{2h_1}...p_x^{2h_x}$.

+) a lẻ: Đặt $a=2t+1$ thì tổng các ước chính phương của n là $(2^0+2^2+...+2^{2t}).\prod_{i=1}^x(p_i^0+p_i^2+...+p_i^{2h_i})\geq 2^{2t}.p_1^{2h_1}.p_2^{2h_2}...p_x^{2h_x}\geq \frac{n}{2}$.

+) a chẵn: Khi đó a - 1 là lẻ. Dễ thấy tổng các ước chính phương của n lớn hơn hoặc bằng tổng các ước chính phương của $\frac{n}{2}$ nên không nhỏ hơn $\frac{n}{4}$.

Vâỵ ta có đpcm.

[LTBN]

Bài 3. (5,0 điểm)

 

Cho tam giác $ABC$, gọi $A_1\,,\,B_1\,,\,C_1$ lần lượt là các điểm đối xứng của $A\,,\,B\,,\,C$ qua $BC\,,\,CA\,,\,AB$

Chứng minh rằng   $A_1\,,\,B_1\,,\,C_1$  thẳng hàng khi và chỉ khi  $cosA\,cosB\,cosC\,\,=\,\,-\frac{3}{8}$

 

Câu hình chủ yếu là bổ đề trong sách NVL

Gọi $H$ là trực tâm tam giác ABC.

Gọi $O$ là tâm $(ABC)$.

Xét phép vị tự tâm O tỉ số 2.

$H^2_O: \mapsto X,B\mapsto Y,C\mapsto Z$.

Gọi $O_a$ là tâm của $(BHC)$. Khi đó $O,O_a$ đối xứng với nhau qua $BC$. Suy ra $O_a\in YZ$. Hiển nhiên $A_1\in (O_a)$ nên $YZ$ là trung trực của $HA_1$, hay $A_1$ là điểm đối xứng của $H$ qua $YZ$.

Tương tự $B_1,C_1$ lần lượt là điểm đối xứng của $H$ qua $ZX,XY$. Suy ra $A_1,B_1,C_1$ thẳng hàng khi và chỉ khi $H$ nằm trên $(XYZ)$, hay $OH=2R$.

Khi đó dễ thấy $H$ nằm ngoài $\Delta ABC$. Giả sử $\angle BAC> 90^o$. HA cắt BC tại D, cắt (O) lại tại E. 

Ta có $3R^2=OH^2-R^2=\wp_{H/(O)}=HA.HE=2HA.HD=2HA^2.\frac{HA}{HD}=8OM^2.\frac{HA}{HB}.\frac{HB}{HD}=8OM^2.\frac{-cosBAC}{cos ABC}.\frac{1}{cos ACB}=8OB^2.cos^2BAC.\frac{-cosBAC}{cos ABC}.\frac{1}{cos ACB}=8R^2.\frac{-1}{cosBACcosABCcosACB}\Rightarrow đpcm$.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi LTBN: 17-10-2021 - 21:37