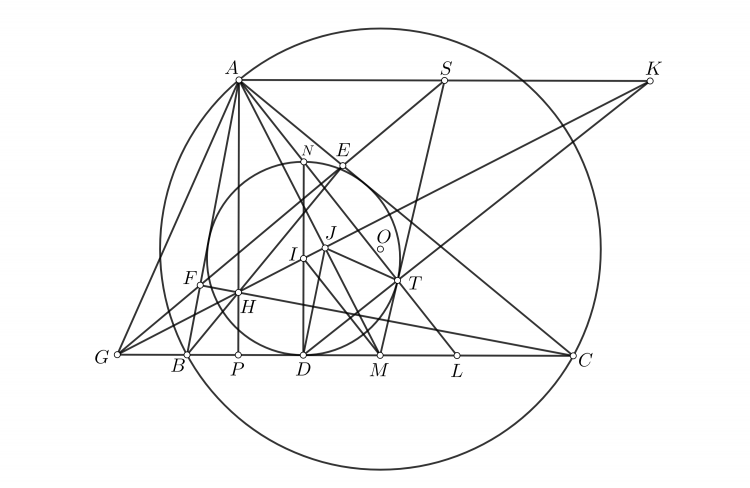
Bổ đề: Cho tam giác ABC nội tiếp (O), hai tiếp tuyến cắt nhau tại V, ba đường cao AD, BE, CF cắt nhau tại H. EF cắt BC tại G, T là trung điểm của AV. Khi đó $\angle AGD+\angle AOT=180^o$.
Chứng minh: Gọi K là trung điểm của BC, M là trung điểm của AH.
Dễ thấy $\angle OAV=\angle MAK$.
Ta có $AM||OV$; $MK||AO$ nên $\angle AMK=\angle AOV$. Từ đó $\Delta AMK\sim\Delta AOV$ nên $\Delta AHK\sim\Delta AOT$.
Từ đó $\angle DHK+\angle AOT=180^o$. Mà H là trực tâm của tam giác AGK (định lý Brocard) nên $\angle AGD+\angle AOT=180^o$. (đpcm)

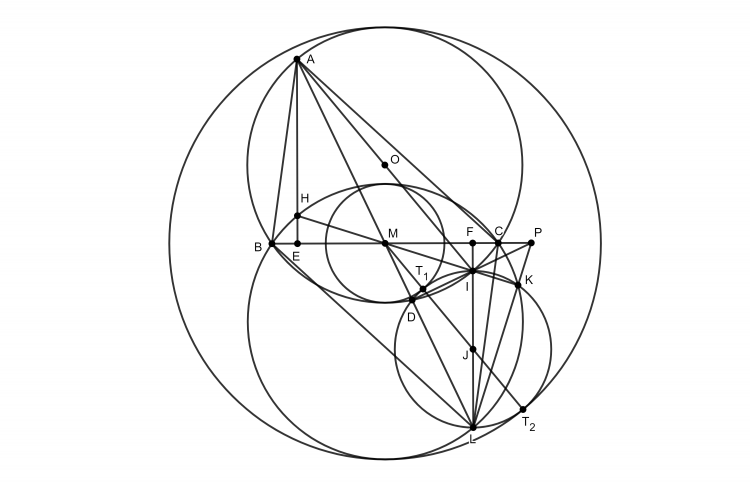
Quay trở lại bài toán:

Gọi L là giao của KP và IM.
Gọi E, F lần lượt là tiếp điểm của $(I)$ trên AC, AB.
Gọi J là $EF\cap BC$.
Ta có kết quả quen thuộc $N\in EF$.
Dễ thấy $\Delta KBF\sim\Delta KCE(g.g)$, suy ra $\frac{KB}{KC}=\frac{BF}{CE}=\frac{BD}{CD}$.
Từ đó KD là phân giác của $\angle BKC$.
Mặt khác $\frac{JB}{JC}=\frac{DB}{DC}$ nên KJ là phân giác ngoài, suy ra $K\in(JD)$.
$\Delta KEF$ có I là điểm chính giữa cung $EF$ của $(KEF)$ nên KI là phân giác của $\angle EKF$.
Gọi $KI$ cắt $EF$ tại N.
Khi đó $\frac{NF}{NE}=\frac{KF}{KE}=\frac{BF}{CE}$ nên $\Delta BFN\sim\Delta CEN$, suy ra EF là phân giác ngoài $\angle BNC$.
Lại có $\frac{NB}{NC}=\frac{BF}{CE}=\frac{BD}{CD}$ nên ND là phân giác trong $\angle BNC$. Suy ra $ND\perp EF$ nên $N\in (JD)$.
KA cắt EF tại Q. Dễ thấy $KA\perp KN$ nên KQ là phân giác ngoài góc EKF.
Biến đổi $\angle QKD=90^o-\angle NKD=90^o-\angle NJD=JPD$.
Suy ra tứ giác QKPD nội tiếp.
Ta có $\frac{QF}{QE}=\frac{KF}{KE}=\frac{NF}{NE}$.
Kẻ đường cao EE' và FF' của tam giác DEF thì K, E', F' thẳng hàng.
Ta có kết quả quen thuộc là IM đi qua trung điểm H của AD. Suy ra theo bổ đề ta có $\angle DQN+\angle DIH=180^o$.
Từ đó $\angle DKP+\angle DIL=180^o$ nên tứ giác KLID nội tiếp.
Kẻ đường cao BB' và CC' của tam giác BIC.
Theo kết quả quen thuộc thì $B',C'\in EF$.
Từ đó tứ giác IC'FB nội tiếp nên tứ giác IC'FD nội tiếp. Suy ra PC' . PF = PI . PD = PL . PK nên tứ giác KLC'F nội tiếp.
Tương tự tứ giác KLEB' nội tiếp.
Khi đó $\angle C'LB'=360^o-\angle C'LK-\angle B'LK=180^o+\angle C'FK-\angle B'PK=180^o-\angle EKF=180^o-\angle BAC;\angle C'DB'=2\angle BIC=180^o-\angle BAC\Rightarrow \angle C'LB'=\angle C'DB'\Rightarrow L\in(C'DB')$
$\boxed{8}$: Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc với $BC$ tại $D$. $M$ là trung điểm của $BC$. Gọi $P$ là giao điểm của $ID$ và $AM$. Đường tròn đường kính $AI$ cắt $(ABC)$ tại $K$. Chứng mình rằng đường trung tuyến ứng với điểm $IM$ và $PK$ cắt nhau tại một điểm thuộc đường tròn Euler tam giác $BIC$.
Bài viết đã được chỉnh sửa nội dung bởi Hoang72: 15-08-2021 - 07:10