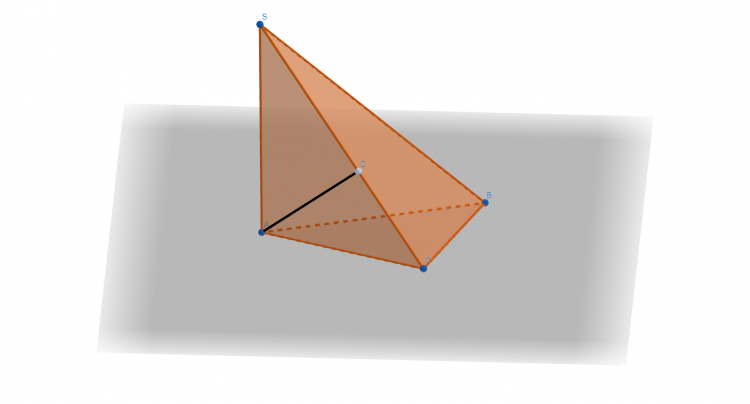
Cho hình chóp tam giác S.ABC có đáy là tam giác ABC vuông tại C, $AC=a$, SA vuông góc với đáy, $SA =a \sqrt 3$. Tính khoảng cách từ điểm A đến mặt phẳng (SBC).
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 03-05-2022 - 04:20
Tiêu đề + LaTeX