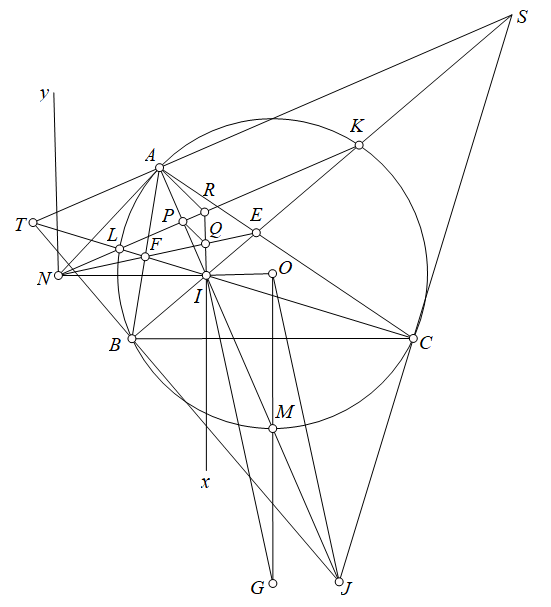
Tam giác $ABC$ nhọn không cân nội tiếp $(O)$ với $I$ là tâm nội tiếp và $BE, CF$ là hai phân giác trong. $BE, CF$ cắt đường tròn $(O)$ tại $K, L$. $AI$ cắt $KL$ ở $P$ và $Q$ trên $EF$ sao cho $QP= QI$ . Chứng minh góc $QIO$ vuông.

Chứng minh góc $QIO$ vuông
#2
 Đã gửi 10-10-2022 - 20:36
Đã gửi 10-10-2022 - 20:36

Định nghĩa lại $Q$ là điểm trên $EF$ sao cho $IQ \perp IO$. Gọi $IQ$ cắt $KL$ tại $R$. Lấy $N$ trên $KL$ sao cho $AN$ tiếp xúc với $(O)$. $M$ là điểm chính giữa cung $BC$. $J,S,T$ lần lượt là tâm bàng tiếp ứng với $A,B,C$ của $\Delta ABC$. $G$ nằm trên $OM$ sao cho $IG \perp EF$.
Ta có $P_{F/(O)}=\overline{FA}.\overline{FB}=\overline{FI}.\overline{FT}=P_{F/(SIT)}$ và $P_{E/(O)}=\overline{EA}.\overline{EC}=\overline{EI}.\overline{ES}=P_{E/(SIT)}$
Suy ra $EF$ là trục đẳng phương của $(SIT)$ và $(O)$. Do đó $EF \perp OJ$ vì $O$ là tâm đường tròn Euler của $\Delta JST$.Suy ra $OJ || IG$. Vì $M$ là trung điểm của $IJ$ nên nó cũng là trung điểm của $OG$. Khi đó chùm $I(OG,Mx)=-1$.
Mặt khác, ta có $\frac{NL}{NK}.\frac{EK}{EI}.\frac{FI}{FL}=\frac{AL^2}{AK^2}.\frac{AK.\sin \angle EAK}{AI.\sin \angle EAI}.\frac{AI.\sin \angle FAI}{AL.\sin \angle FAL}=1$ nên $E,F,N$ thẳng hàng. Dễ chứng minh $IN || BC$. Ta thấy $Ny \perp IO, NQ \perp IG, NR \perp IM, NI \perp Ix$ và $I(OG,Mx)=-1$ nên $N(yQ,RI)=-1$. Từ đó $Q$ là trung điểm của $IR$. Suy ra $PQ$ là đường trung bình song song với $AR$ của $\Delta AIR$. Mà $RA=RI$ nên $QI=QP$, ta thu được điều phải chứng minh.
- Math04 yêu thích
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh