Kết quả bạn tìm ra vẫn đúng trong trường hợp tổng quát, chỉ là cần phải cẩn thận khi xử lý các tỉ số một "xíu" 
========
Để tiện lợi, ta ký hiệu thể tích một hình $\mathcal P$ là $[\mathcal P]$. Trước hết, ta cần bổ đề sau:
Cho tứ diện $OABC$. Trên tia $OA, OB, OC$ lần lượt lấy $A_1, B_1,C_1$. Khi đó \[\frac{{\left[ {O{A_1}{B_1}{C_1}} \right]}}{{\left[ {OABC} \right]}} = \frac{{O{A_1}}}{{OA}}\frac{{O{B_1}}}{{OB}}\frac{{O{C_1}}}{{OC}}\]
Quay lại bài toán, ta cần xây dựng thêm nhiều tứ diện phụ trợ để áp dụng bổ đề trên.
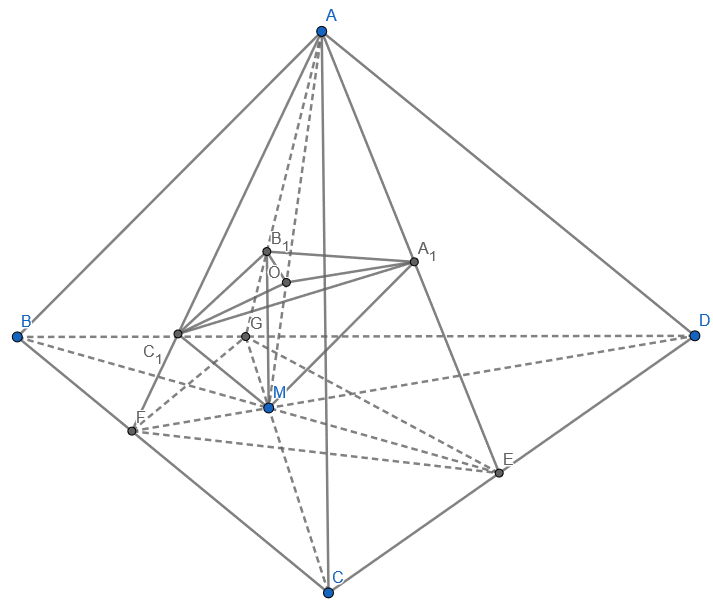
Vẽ $BM,CM,DM$ lần lượt cắt $CD,DB,BC$ tại $E,G,F$. Dễ thấy $AE,EG,AF$ lần lượt chứa $A_1,B_1,C_1$.
Vẽ $AM$ cắt mặt phẳng $A_1B_1C_1$ tại $O$. Ta có: \[\left[ {M{A_1}{B_1}{C_1}} \right] = \left[ {MO{A_1}{B_1}} \right] + \left[ {MO{B_1}{C_1}} \right] + \left[ {MO{C_1}{A_1}} \right]\]
Ta sẽ đi tính tỉ lệ của thể tích từng khối tứ diện con trong vế phải đối với $ABCD$.
\[\begin{gathered}
\frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {MAEG} \right]}} = \frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {MA{A_1}{B_1}} \right]}}\frac{{\left[ {MA{A_1}{B_1}} \right]}}{{\left[ {MAEG} \right]}} = \frac{{MO}}{{MA}}\frac{{A{A_1}}}{{AE}}\frac{{A{B_1}}}{{AG}} \hfill \\
\frac{{\left[ {MAEG} \right]}}{{\left[ {ABCD} \right]}} = \frac{{\left[ {AMEG} \right]}}{{\left[ {ACEG} \right]}}\frac{{\left[ {ACEG} \right]}}{{\left[ {ACDG} \right]}}\frac{{\left[ {ACDG} \right]}}{{\left[ {ABCD} \right]}} = \frac{{GM}}{{GC}}\frac{{CE}}{{CD}}\frac{{DG}}{{DB}} \hfill \\
\Rightarrow \frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{MO}}{{MA}}\frac{{A{A_1}}}{{AE}}\frac{{A{B_1}}}{{AG}}\frac{{GM}}{{GC}}\frac{{CE}}{{CD}}\frac{{DG}}{{DB}} \hfill \\
\end{gathered} \]
Nhìn có vẻ "ghê gớm" vế phải nhưng ta sẽ rút gọn bằng cách sử dụng Thales với những căp đường thẳng song song $MA_1 \parallel AB, MB_1 \parallel AC$.
\[\frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{MO}}{{MA}}\frac{{BM}}{{BE}}\frac{{CM}}{{CG}}\frac{{GM}}{{GC}}\frac{{CE}}{{CD}}\frac{{DG}}{{DB}} \quad (1)\]
Nhìn vẫn còn "khủng", nhưng ta đã làm xuất hiện những tỉ số "liên quan" tới $M$ trên cùng mặt phẳng $BCD$. Ta sẽ tìm cách đơn giản hóa hơn nữa.
Với nhiều đường thẳng đồng quy này, ta thường dùng đến Ceva và Menelaus.
Thật vậy, áp dụng Menalaus cho $\Delta MBG$ với cát tuyến $DEC$: \[\frac{{CM}}{{CG}}\frac{{DG}}{{DB}}\frac{{EB}}{{EM}} = 1 \Rightarrow \frac{{CM}}{{CG}}\frac{{DG}}{{DB}} = \frac{{EM}}{{EB}}\]
Tương tự, $\Delta MED$ với cát tuyến $BFC$: \[\frac{{BM}}{{BE}}\frac{{CE}}{{CD}}\frac{{FD}}{{FM}} = 1 \Rightarrow \frac{{BM}}{{BE}}\frac{{CE}}{{CD}} = \frac{{FM}}{{FD}}\]
Do đó:
\[\left( 1 \right) \Rightarrow \frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{MO}}{{MA}}\frac{{GM}}{{GC}}\left( {\frac{{CM}}{{CG}}\frac{{DG}}{{DB}}} \right)\left( {\frac{{BM}}{{BE}}\frac{{CE}}{{CD}}} \right) = \frac{{MO}}{{MA}}\frac{{GM}}{{GC}}\frac{{EM}}{{EB}}\frac{{FM}}{{FD}}\]
Tương tự ta có:
\[\frac{{\left[ {MO{A_1}{B_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{\left[ {MO{B_1}{C_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{\left[ {MO{C_1}{A_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{MO}}{{MA}}\frac{{GM}}{{GC}}\frac{{EM}}{{EB}}\frac{{FM}}{{FD}}\]
Vậy nên: \[\frac{{\left[ {M{A_1}{B_1}{C_1}} \right]}}{{\left[ {ABCD} \right]}} = 3\frac{{MO}}{{MA}}\frac{{GM}}{{GC}}\frac{{EM}}{{EB}}\frac{{FM}}{{FD}} \quad (2)\]

Tiếp theo, ta để ý một tính chất đặc biệt: $O$ là trọng tâm $\Delta A_1B_1C_1$ và $\frac{MO}{MA} = \frac{1}{3}$.
Để chứng minh điều này, ta vẽ $FG$ cắt $BM$ tại $H$, $AH$ cắt $B_1C_1$ tại $K$. Dễ thấy $A_1,O,K$ thẳng hàng.
Vẽ $MK$ cắt $AB$ tại $P$. Do $M{B_1}\parallel AC$ và $MC_1\parallel AD$ nên $(MB_1C_1) \parallel (ACD)$. Vì thế:
\[\begin{gathered}
{C_1}P = \left( {ABC} \right) \cap \left( {M{B_1}{C_1}} \right)\parallel \left( {ABC} \right) \cap \left( {ACD} \right) = AC \hfill \\
{B_1}P = \left( {ABD} \right) \cap \left( {M{B_1}{C_1}} \right)\parallel \left( {ABD} \right) \cap \left( {ACD} \right) = AD \hfill \\
\end{gathered} \]
Vậy $MB_1PC_1$ là hình bình hành. Tức $K$ là trung điểm $MP$ và $B_1C_1$.
Mặt khác, $MK = \left( {ABE} \right) \cap \left( {M{B_1}{C_1}} \right)\parallel \left( {ABE} \right) \cap \left( {ACD} \right) = AE$.
Mà $MA_1 \parallel AB \Rightarrow MA_1AP$ là hình bình hành. Do đó $\frac{{OM}}{{OA}} = \frac{{MK}}{{A{A_1}}} = \frac{{MK}}{{MP}} = \frac{1}{2}$.
Ta suy ra $O$ là trọng tâm $\Delta A_1B_1C_1$ và $\frac{{MO}}{{MA}} = \frac{{MO}}{{OA + MA}} = \frac{1}{{1 + 2}} = \frac{1}{3}$.
Kết hợp với $(2)$, ta thu được: \[\frac{{\left[ {M{A_1}{B_1}{C_1}} \right]}}{{\left[ {ABCD} \right]}} = \frac{{GM}}{{GC}}\frac{{EM}}{{EB}}\frac{{FM}}{{FD}}\]
Lại chú ý rằng, 3 tỉ số này có tính chất đặc biệt là:\[\frac{{GM}}{{GC}} + \frac{{EM}}{{EB}} + \frac{{FM}}{{FD}} = \frac{{{S_{BMD}}}}{{{S_{BCD}}}} + \frac{{{S_{DMC}}}}{{{S_{DBC}}}} + \frac{{{S_{BCM}}}}{{{S_{CBD}}}} = 1\]
Nên \[\frac{{\left[ {M{A_1}{B_1}{C_1}} \right]}}{{\left[ {ABCD} \right]}} \leqslant \frac{1}{{27}}{\left( {\frac{{GM}}{{GC}} + \frac{{EM}}{{EB}} + \frac{{FM}}{{FD}}} \right)^3} = \frac{1}{{27}}\]
=========
Ta có thể chứng minh $O$ là trọng tâm $A_1B_1C_1$ trước để thu được ngay một tính chất quan trọng của trọng tâm: $S_{OA_1B_1}=S_{OB_1C_1}=S_{OC_1A_1}$, từ đó ta có $[MOA_1B_1]=[MOB_1C_1]=[MOC_1A_1]$.









