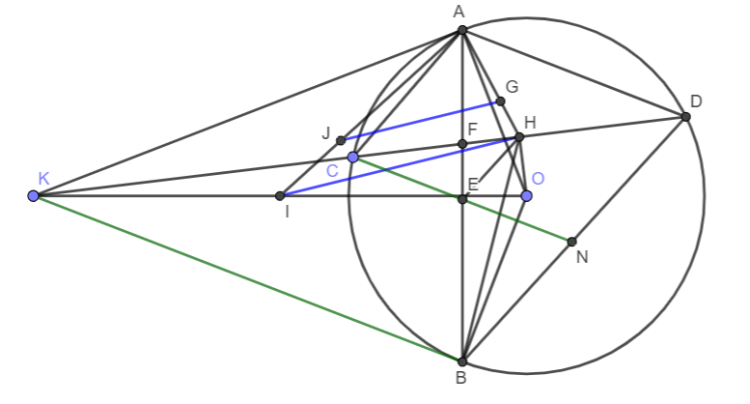
a) Dễ dàng chứng minh được $\angle KHO=\angle KAO=\angle KBO = 90^{\circ}$. Các điểm $A, B, H$ cùng nhìn $KO$ dưới một góc bằng 90 độ nên $A, B, K, H, O$ cùng thuộc một đường tròn.
b) $\bigtriangleup KAC\sim\bigtriangleup KDA \quad(\angle CKA=\angle AKD,\angle AKC=\angle KDA)\Rightarrow \frac{KA}{KD}=\frac{AC}{DA} \Rightarrow AD.AK=AC.KD$.
c) Xét tứ giác $ACEH$ có $\angle AHC\equiv \angle AHK=\angle ABK=\angle AEC$ nên $ACEH$ là tứ giác nội tiếp, suy ra$\angle AEH=\angle ACH\equiv \angle ACD=\angle ABD$, suy ra $EH\parallel BD$.
Xét $\bigtriangleup CND$ có $EH\parallel ND$, $H$ là trung điểm $CD$ nên $E$ là trung điểm của $CN$, hay $EC=EN$.
d) Gọi $I$ là trung điểm của $KO$, $J$ là trọng tâm tam giác $AKO$. Khi đó có $I, J$ cố định, $JA=\frac{2}{3}AI=\frac{1}{3}KO$. (1)
Xét $\bigtriangleup AHI$ có $\frac{AJ}{AI}=\frac{AG}{AH}=\frac{2}{3}$ nên $JG\parallel IH\Rightarrow JG=\frac{2}{3}IH=\frac{1}{3}KO$. (2)
Từ (1) và (2) suy ra $G\in(J,JA)$ cố định hay $G$ di chuyển trên $(J,JA)$ (Giới hạn: $G$ thuộc cung bị chia bởi $AB$ không thuộc nửa mặt phẳng chứa điểm $K$).
Bài viết đã được chỉnh sửa nội dung bởi Leonguyen: 12-03-2023 - 15:29