PHẦN I. GIỚI THIỆU
ĐỊNH LÝ PYTAGO. Trong một tam giác vuông bình phương cạnh huyền bằng tổng của bình phương hai cạnh góc vuông.
Một định lý quá nổi tiếng và cũng là một trong số những định lý quan trọng bậc nhất trong hình học sơ cấp. Có rất nhiều cách chứng minh, tuy nhiên một tài liệu hệ thống đầy đủ và toàn diện các cách giải đã được tìm ra dường như là rất hiếm. Hiện tại mình mới chỉ biết trang sau có tổng hợp được tất cả 118 cách: https://www.cut-the-...org/pythagoras/.
Trong bài viết dưới đây, mình tuyển chọn ra từ tài liệu trên 7 cách giải tiêu biểu với đặc điểm chung là vận dụng tính chất của hai tam giác đồng dạng. Lý do trước tiên mình chọn hướng đi này là vì mình thấy cách dùng hai tam giác đồng dạng đơn giản hơn phần lớn các cách giải khác. Hãy xem ngay cách đầu tiên, khó có cách giải nào ngắn gọn hơn thế được. Lý do tiếp theo, mình thấy những cách giải này nói chung không quá phổ biến (nhất là so với các cách giải bằng ghép hình vốn chỉ cần dùng tới kiến thức của toán 7). Vì vậy, việc giới thiệu nó tới mọi người chắc hẳn sẽ có chút giá trị đóng góp nào đó.
Một vấn đề cần cũng nói thêm đó là trong tài liệu gốc ở trên có nhiều cách mình nghĩ thực chất chỉ là một, nói chung chúng chỉ là được phát biểu hay trình bày khác đi mà thôi. 7 cách mình giới thiệu sau đây, đã được cân nhắc tuyển chọn tương đối kỹ lưỡng để tránh tình trạng trùng lặp trên. Một cách giải đúng nghĩa phải có những yếu tố độc đáo của riêng nó.
So với tài liệu gốc, mình giữ nguyên ý tưởng chứng minh, nhưng đã vẽ lại hình và sửa đổi cách trình bày sao cho vừa đủ đơn giản nhưng vẫn nổi bật lên các kiến thức quan trọng được vận dụng. Tất cả các cách đều thống nhất xét tam giác ABC vuông tại A. Bây giờ mời mọi người thưởng thức 7 cách chứng minh cho định lý thật đẹp này!
PHẦN II. 7 CÁCH CHỨNG MINH ĐỊNH LÝ PYTAGO
CÁCH 1. Đây là cách đơn giản nhất vận dụng hai tam giác đồng dạng. Câu hỏi đặt ra là: nếu ta đã có một cách giải đơn giản đến thế này thì tại sao lại còn phải đi tìm thêm các cách khác thậm chí dài dòng và phức tạp hơn? Khó mà trả lời được cho thoả đáng. Dường như ta đi tìm một lời giải khác chỉ đơn giản vì điều đó là có thể. Có nhiều con đường để đến cùng một cái đích và trên mỗi con đường ta lại có những trải nghiệm khác nhau, đôi khi ta sẽ phải đi dài hơn, nhưng điều đó là xứng đáng.
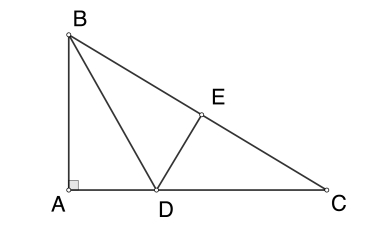
Kẻ đường cao AD của tam giác ABC. Dễ thấy, hai tam giác DBA và DAC đều đồng dạng với tam giác ABC. Từ tỉ số bằng nhau giữa các cạnh tương tứng ta suy ra $AB^2=BD.BC$ và $AC^2=CD.BC.$ Do đó $AB^2+AC^2=(BD+CD).BC=BC^2.$ Đây là điều phải chứng minh.
CÁCH 2.
Lấy D thuộc tia BC và E thuộc tia đối tia BC sao cho $BD=BE=AB.$ Khi đó tam giác EAD vuông tại A. Vì $\angle DAE=\angle BAC=90^{\circ}$ nên $\angle BAE=\angle DAC$. Hơn nữa, ta lại có $\angle BAE=\angle BEA$ (vì tam giác BAE cân tại B), do đó $\angle CAD=\angle BEA.$ Như vậy tam giác CDA và tam giác CAE đồng dạng, từ đó ta có $AC^2=CD.CE.$ Để ý rằng $CD=BC-BD=BC-AB$ và $CE=BC+BE=BC+AB.$ Ta suy ra $ AC^2=(BC-AB)(BC+AB)$ hay $AC^2=BC^2-AB^2$. Ta có điều phải chứng minh.
CÁCH 3.
Kẻ tia phân giác BD của góc ABC, E là hình chiếu của D trên BC. Khi đó tam giác EDC đồng dạng với tam giác ABC (g.g), suy ra $AC.CD=CE.BC.$ Vì BD là tia phân giác của góc ABC nên $CD= \frac{AC.BC}{AB+BC}.$ Ta còn thấy rằng tam giác ABD bằng tam giác EBD (cạnh huyền-góc nhọn) nên $BE=AB$, từ đó suy ra $CE=BC-BE=BC-AB.$ Như vậy
$AC. \frac {AC.BC}{AB+BC}=(BC-AB).BC.$
Điều này tương đương với
$AC^2=(AB+BC)(BC-AB)=BC^2-AB^2.$
Ta có điều phải chứng minh.
CÁCH 4.
Gọi D là trung điểm BC, qua A kẻ đường thẳng d vuông góc AD; E, F lần lượt là hình chiếu của B và C trên đường thẳng d.
Hình thang BEFC có D là trung điểm cạnh bên BC, AD lại song song với hai đáy, cho nên A là trung điểm EF. Như vậy ta có $AE=AF=\frac{EF}{2}.$ Ta lại có BEFC là hình thang vuông có đường cao EF nên $S_{BEFC}= \frac{1}{2}.EF.(BE+FC).$
Hai tam giác BEA và AFC có tổng diện tích là
$S_{BEA}+S_{AFC}=\frac{1}{2}.AE.BE+\frac{1}{2}.AF.FC=\frac{1}{2}.\frac{EF}{2}.(BE+FC)= \frac{1}{2}.S_{BEFC}$.
Mặt khác, hai đoạn thẳng AB và AC chia tứ giác BEFC thành 3 tam giác là ABC, EBA, FAC cho nên $S_{BEFC} =S_{EBA}+ S_{FAC}+S_{ABC}$. Vì vậy $S_{EBA}+ S_{FAC}= S_{ABC}.$
Dễ thấy tam giác EBA và tam giác FAC đều đồng dạng với tam giác ABC. Do đó $\frac{S_{EBA}}{S_{ABC}}=\left ( \frac{AB}{BC} \right )^{2}$ và $\frac{S_{FAC}}{S_{ABC}}=\left ( \frac{AC}{BC} \right )^{2}.$
Vậy ta có $\left ( \frac{AB}{BC} \right )^{2}+\left ( \frac{AC}{BC} \right )^{2}=1$ hay $AB^2+AC^2=BC^2.$ Đây là điều phải chứng minh.
CÁCH 5.
Trên tia đối của tia AB lây điểm D sao cho $BD=BC.$ Gọi E là giao điểm của đường thẳng đi qua D vuông góc với AD và tia phân giác của góc DBC. F là hình chiếu của E trên đường thẳng AC.
Dễ thấy tam giác DBE và tam giác CBE bằng nhau (c.g.c) do đó $DE=CE$ và $\angle BCE=\angle BDE=90^{\circ}.$ Từ đây ta có tam giác ABC đồng dạng với tam giác FCE. Suy ra $CE=EF.\frac{BC}{AC}$ và $CF=EF.\frac{AB}{AC}.$
Để ý rằng ADEF là hình chữ nhật nên $CE=DE=AC+CF.$ Do đó $CE-CF=AC$, điều này tương đương $\frac{EF.(BC-AB)}{AC}=AC.$ Mặt khác, ta lại có $EF=BD+AB=BC+AB.$ Vì vậy $\frac{(BC+AB)(BC-AB)}{AC}=AC.$ Từ đây ta suy ra ngay điều phải chứng minh.
CÁCH 6.
Đặt $BC=a$, $AC=b$ và $AB=c.$ Trên tia đối của CA lấy điểm E sao cho $CE=CB=a$, trên tia đối của CB lấy điểm D sao cho $CD=CA=b.$ Dễ thấy hai tam giác ABC và EDC bằng nhau (c.g.c) , do đó $DE=AB=c$ và $ \angle ABC=\angle DEC.$
Tiếp theo, lấy điểm M trên đoạn BC sao cho $BM=BA=c$, điểm E trên tia đối của tia EC sao cho $EN=DE=c.$ DEC là góc ngoài tại đỉnh E của tam giác cân DEN nên $\angle DNE=\frac {\angle DEC}{2}.$ Tam giác BAM cân tại B nên $\angle BAM=90^{\circ}- \frac{\angle ABC}{2}.$ Do đó $\angle CAM=\frac {\angle ABC}{2}.$ Mà $\angle DEC=\angle ABC$ nên $\angle DNE=\angle CAM.$ Do đó AM song song DN.
Áp dụng Định lý Thales ta có $\frac {AC}{CN}=\frac {MC}{CD}.$ Để ý rằng $CN=a+c$ và $CM=a-c$, ta suy ra $\frac {b}{a+c}=\frac {a-c}{b}$ hay $a^2=b^2+c^2.$ Đây là điều phải chứng minh.
CÁCH 7.
Đặt $AB=c$, $AC=b$ và $BC=a.$
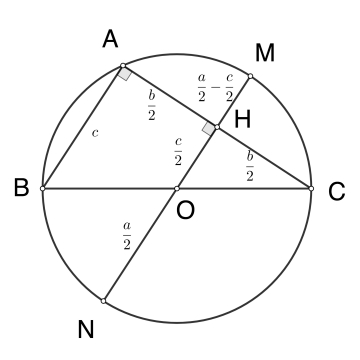
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, khi đó O là trung điểm BC. Qua O kẻ đường kính MN vuông góc với AC tại H. Dễ thấy H là trung điểm AC nên $HA=HC=\frac{b}{2}$; OH là đường trung bình của tam giác ABC nên $OH=\frac{c}{2}$; MN là đường kính đường tròn nên $OM=ON=\frac{a}{2}$. Từ đó ta tính được $MH=\frac{a}{2}-\frac{c}{2}$ và $NH=\frac{a}{2}+\frac{c}{2}.$
Ta có $\angle MAH=\angle CNH$ (hai góc nội tiếp cùng chắn cung MC). Suy ra tam giác AHM đồng dạng tam giác CHN (g.g), vì vậy $AH.HC=HM.HN.$ Điều này tương đương $ \frac{b}{2}.\frac{b}{2}=\left ( \frac{a}{2}-\frac{c}{2} \right ). \left (\frac{a}{2}+\frac{c}{2} \right ).$ Từ đó suy ra điều phải chứng minh.
Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 13-05-2023 - 10:46