$LOVE(x)|_{x =\alpha}^\Omega=+\infty$
Thầy @thvn nói về các bài toán "căn bản" trong hình học THCS làm mình nhớ ngày xưa có vài bài thú vị cho lớp 6,7 
1) Cho tam giác $ABC$ nhọn. Trên $BC$ lấy $D, E$ sao cho $\angle BAD = \angle DAE = \angle EAC$. Trong 3 đoạn thẳng $BD,DE,EC$, đoạn nào dài nhất?
Và bài toán "đảo":
2) Cho tam giác $ABC$ nhọn. Trên $BC$ lấy $D,E$ sao cho $BD=DE=EC$. Trong 3 góc $\angle BAD, \angle DAE, \angle EAC$, góc nào nhỏ nhất?
Sĩ quan
Thầy @thvn nói về các bài toán "căn bản" trong hình học THCS làm mình nhớ ngày xưa có vài bài thú vị cho lớp 6,7
1) Cho tam giác $ABC$ nhọn. Trên $BC$ lấy $D, E$ sao cho $\angle BAD = \angle DAE = \angle EAC$. Trong 3 đoạn thẳng $BD,DE,EC$, đoạn nào dài nhất?
Mấy bài kiểu này rất thú vị! Sau đây mình giải phần 1).
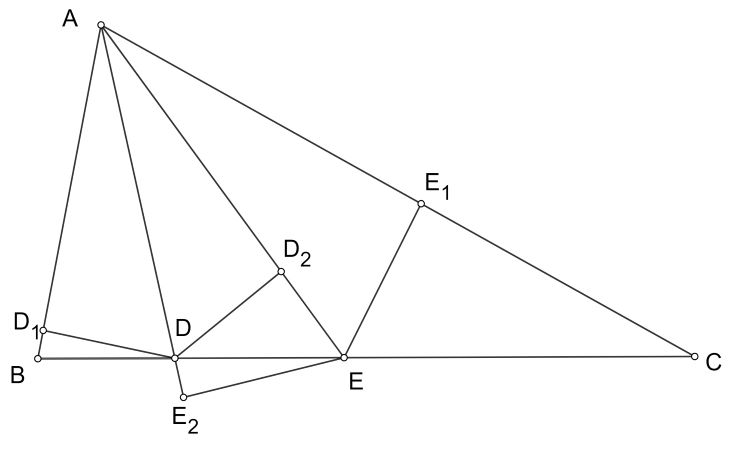
a) Xét trường hợp tam giác $ABC$ có hai cạnh $AB, AC$ độ dài khác nhau. Không mất tính tổng quát giả sử $AB < AC$. Ta sẽ chứng minh $EC$ có độ dài lớn hơn $BD$ và $ED$.
* Chứng minh $BD<EC$.
Theo quan hệ giữa góc và cạnh đối diện trong tam giác, vì $AB<AC$ nên $\angle C<\angle B$.
Ta có $\angle ADE$ là góc ngoài tam giác $ADB$, còn $\angle AED$ là góc ngoài tam giác $AEC$. Hơn nữa $\angle BAD=\angle CEA$ và $\angle C<\angle B$. Do đó $\angle AED<\angle ADE$. Vì vậy $AD<AE$.
Tiếp theo, gọi $D_1, D_2$ lần lượt là chân đường vuông góc hạ từ $D$ xuống $AB, AE$; $E_1, E_2$ lần lượt là chân đường vuông góc hạ từ $E$ xuống $AC, AD$.
Do $AD$ là tia phân giác của góc $BAE$, $AE$ là tia phân giác của góc $DAC$ nên ta có ngay $DD_1=DD_2$ và $EE_1=EE_2$.
Ta có $DD_2.AE=EE_2.AD=2S_{ADE}$. Mà $AD<AE$ nên $DD_2<EE_2$ hay $DD_1<EE_1$.
Ta lại có $AB<AC$ nên $AB.DD_1<AC.EE_1$ hay $S_{ABD}<S_{AEC}$.
Mà $\frac{BD}{EC}=\frac{S_{ABD}}{S_{AEC}}$. Chứng tỏ $BD<EC$.
*Chứng minh $ED<EC$.
Ta có $\angle ADC>\angle B>\angle C$. Do đó $AC>AD$. Mà $\frac{ED}{EC}=\frac{AD}{AC}$ ($AE$ là tia phân giác của góc $CAD$). Chứng tỏ $ED < EC$.
b) Trường hợp $AB=AC$, khi đó tam giác $ABD$ bằng tam giác $ACE$ (g.c.g), suy ra $BD=EC$. Chứng minh tương tự như trường hợp a) ta có $ED<BD=EC$.
____
Chứng minh trên không cần tới giả thiết tam giác $ABC$ nhọn. Liệu có bị thiếu sót ở đâu không?
Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 24-05-2023 - 01:24
$LOVE(x)|_{x =\alpha}^\Omega=+\infty$
Một lời giải đẹp Thú thật thì bài toán này quá lâu rồi, mình không nhớ rõ chi tiết. Nhưng dữ kiện "$\Delta ABC$ nhọn" thường hay xuất hiện trong các bài toán lớp 6,7 để các em đỡ phải chứng minh những trường hợp ngoại lệ 
Tuy nhiên tìm được cách chứng minh tổng quát thì càng tốt 
0 thành viên, 1 khách, 0 thành viên ẩn danh
Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học
