Chủ đề này có 4 trả lời

[hoaian2014]

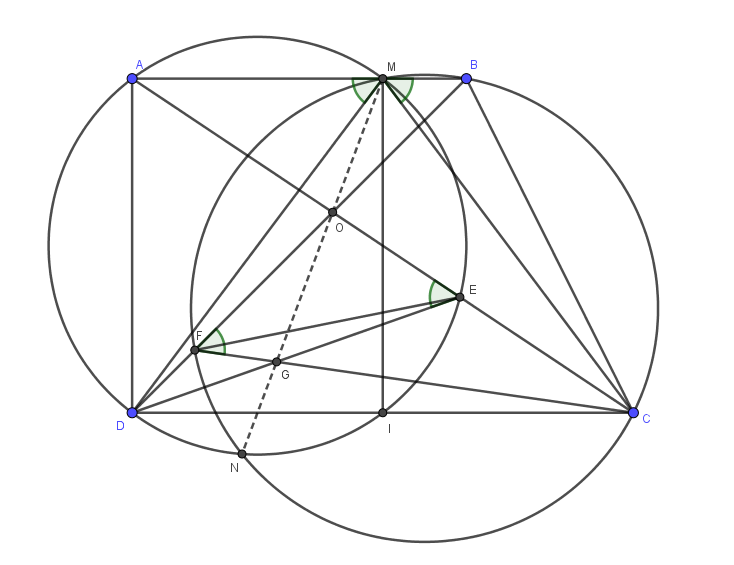
Cho hình thang $ABCD$ có $AB$ là đáy nhỏ ($AD< AC, BC< BD$). Trên cạnh $AB$ lấy điểm $M$ sao cho tam giác $MCD$ cân tại $M$ . Gọi $O$ là giao điểm của $AC$ và $BD$. Gọi $E$ là giao điểm thứ hai của $AC$ với đường tròn $(O_1)$ ngoại tiếp tam giác $ADM$ , $F$ là giao điểm thứ hai của $BD$ với đường tròn $(O_2)$  ngoại tiếp tam giác $BCM$ . $N$ là giao điểm thứ hai của $(O_1)$ và $(O_2)$
a) Chứng minh tứ giác $DCEF$ nội tiếp đường tròn.
b) Chứng minh ba điểm $M, N, O$  thẳng hàng.
 

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 29-05-2023 - 00:54
Tiêu đề & LaTeX

[William Nguyen]

a, Chứng minh tứ giác $DCEF$ nội tiếp:

• Gọi $I$ là trung điểm $CD$
• $\bigtriangleup MCD$ cân tại $M$ $\Rightarrow MI \perp CD \Rightarrow MI \perp AB$
• $\widehat{DMI} = \widehat{CMI} \Rightarrow \widehat{AMD} = \widehat{BMC}$
• Tứ giác $AMED$ nội tiếp $\Rightarrow \widehat{AMD} = \widehat{AED}$
• Tứ giác $BMFC$ nội tiếp $\Rightarrow \widehat{BMC} = \widehat{BFC}$
• Do đó $\widehat{AED} = \widehat{BFC} \Rightarrow \widehat{DEC} = \widehat{DFC}$

Ta có điều phải chứng minh.

b, Trong quá trình vẽ hình mình phát hiện có thể "nâng cấp" độ khó như sau:

    Gọi $G$ là giao điểm của $DE$ và $CF$, chứng minh bốn điểm $M, O, G, N$ thẳng hàng.

Còn lời giải cho phần này mình chưa nghĩ ra, có thể sử dụng phương tích chăng?

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi William Nguyen: 28-05-2023 - 20:48

[perfectstrong]

$C,D,E,F$ đồng viên nên $\overline{GC}.\overline{GF}=\overline{GD}.\overline{GE} \Rightarrow \mathcal{P}_{G/(O_2)}=\mathcal{P}_{G/(O_1}$ (1).

$AB \parallel CD \Rightarrow (AB;AC) = (CD;CA) = (FB;FE) (\text{mod } \pi)$ (do $C,D,E,F$ đồng viên). Do đó $A, B, E, F$ đồng viên.

Vì thế $\overline{OA}.\overline{OE} =\overline{OB}.\overline{OF} \Rightarrow \mathcal{P}_{O/(O_2)}=\mathcal{P}_{O/(O_1)}$ (2).

Từ (1), (2) suy ra $O,G$ thuộc $MN$, trục đẳng phương của $(O_1)$ và $(O_2)$.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 29-05-2023 - 17:13

[William Nguyen]

$C,D,E,F$ đồng viên nên $\overline{GC}.\overline{GF}=\overline{GD}.\overline{GE} \Rightarrow \mathcal{P}_{G/(O_2)}=\mathcal{P}_{G/(O_1}$ (1).

$AB \parallel CD \Rightarrow (AB;AC) = (CD;CA) = (FB;FE) (\text{mod } \pi)$ (do $C,D,E,F$ đồng viên). Do đó $A, B, E, F$ đồng viên.

Vì thế $\overline{OA}.\overline{OE} = \overline{OB}.\overline{OB}.\overline{OF} \Rightarrow \mathcal{P}_{O/(O_2)}=\mathcal{P}_{O/(O_1}$ (2).

Từ (1), (2) suy ra $O,G$ thuộc $MN$, trục đẳng phương của $(O_1)$ và $(O_2)$.

Hình như dòng 3 thừa 1 lần $\overline{OB}$ rồi ạ, với cả ở hình cấp 2 em chưa biết có định lý phương tích như vậy, chỉ có nếu $O, M, N$ thẳng hàng thì có $OA.OE = OM.ON = OB.OF$ thôi, định lý này được dùng luôn khi thi hsg không ạ?

[perfectstrong]

Đúng ra thì độ dài đại số, góc định hướng, phương tích, và cả trục đẳng phương không được dạy ở cấp phổ thông nên không thể sử dụng trực tiếp được.

Bạn có thể dùng một cách gián tiếp (chứng minh lại trục đẳng phương): chuyển đổi phương tích thành dạng bình phương khoảng cách trừ bình phương bán kính, sau đó chứng minh là $\overrightarrow{GN}.\overrightarrow{O_1O_2} = 0$ để có $GN \perp O_1O_2$, rồi tương tự với $O$.