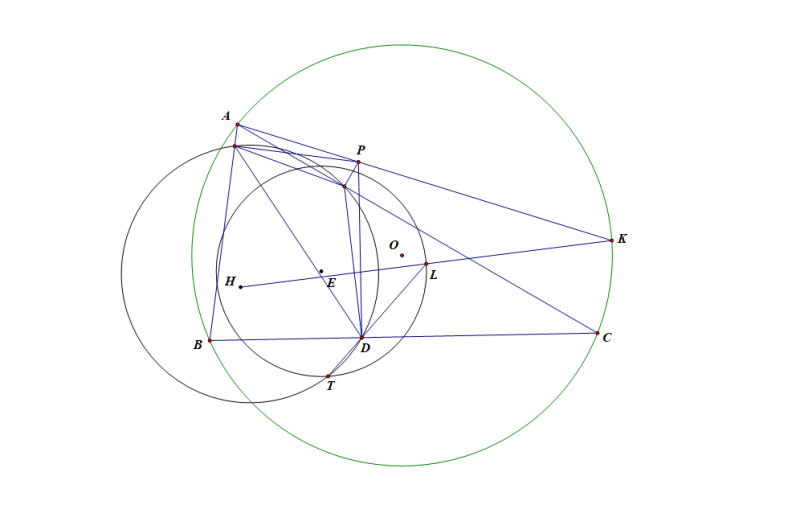
Cho tam giác $ABC$ nội tiếp $(O)$, trực tâm $H$, đường tròn $(E)$ là đường tròn $Euler$ của tam giác $ABC$. Hai điểm $T$ và $L$ trên $(E)$, $TL$ cắt $BC$ tại $D$, $HL$ cắt $(O)$ tại $K$. Điểm $P$ trên $AK$ thỏa mãn $PD$ vuông góc với $BC$. Chứng minh rằng $T$ nằm trên đường tròn $pedal$ của điểm $P$ ứng với tam giác $ABC$.
Trước khi đưa ra chứng minh, mình có nhiều lời bình luận về phát biểu của bài toán. Mình không thích cách phát biểu này, vì mấy lý do sau
- trong phát biểu này, hai đối tượng điều khiển là $T$ và $L$, còn $P$, $D$, $K$ phụ thuộc vào $P$
- $HL$ cắt $(O)$ tại $K$ không phải một phát biểu chặt chẽ vì đường thẳng và đường tròn có thể có nhiều nhất 2 hai giao điểm. Trong bài toán này, $K$ nên được định nghĩa là điểm đối xứng với $H$ qua $L$
- Bài toán có thể được phát biểu lại để đối tượng điều khiển duy nhất là điểm $P$.
Mình phát biểu lại bài toán như sau (và thay đổi tên điểm)
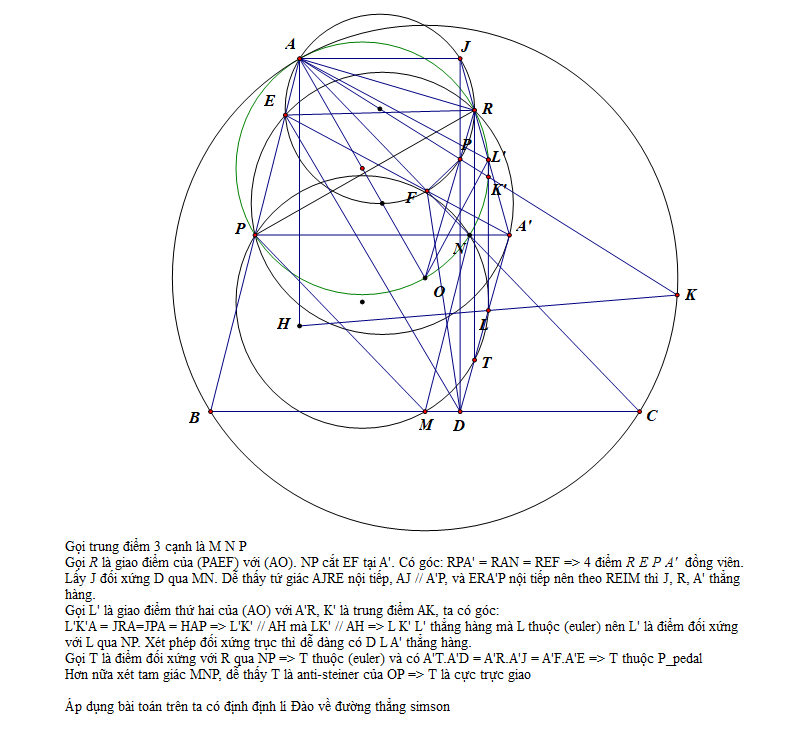
Cho tam giác $ABC$ nội tiếp đường tròn tâm $O$. $H$ là trực tâm của tam giác $ABC$. $P$ là một điểm không nằm trên đường tròn ngoại tiếp tam giác $ABC$ và $P\ne O$.
$P_{a}$, $P_{b}$, $P_{c}$ lần lượt là hình chiếu vuông góc của $P$ lên các đường thẳng $BC$, $CA$, $AB$.
$T$ là cực trực giao (bạn đọc hay tra cứu với từ khóa orthopole) của đường thẳng $OP$ với tam giác $ABC$. $A_{p}$ và $A$ là hai giao điểm của $AP$ với đường tròn ngoại tiếp tam giác $ABC$. $A'_{p}$ là trung điểm của đoạn thẳng $HA_{p}$.
Chứng minh rằng ba điểm $T$, $P_{a}$, $A'_{p}$ thẳng hàng.
Mình sẽ chứng minh không dùng và không phu thuộc hình vẽ. Ý tưởng của mình là sử dụng các định lý Fontene, các tính chất của đường thẳng Wallace-Simson và sử dụng góc định hướng.
Chứng minh. Trước khi đi vào phần chứng minh chính, mình nêu lại các tính chất, định lý kinh điển và không chứng minh lại.
Định lý 1. $P, Q$ là hai điểm thuộc đường tròn ngoại tiếp của tam giác $ABC$ thì góc định hướng giữa hai đường thẳng Wallace-Simson $s(ABC, P)$ và $s(ABC, Q)$ của $P$, $Q$ với tam giác $ABC$ có tính chất sau
\[ (s(ABC, P), s(ABC, Q)) \equiv -\frac{1}{2}(\overrightarrow{OP}, \overrightarrow{OQ}) \pmod{\pi}. \]
Định lý 2. Trong một tam giác, đường tròn chín điểm là ảnh của đường tròn ngoại tiếp qua phép vị tự hệ số $\frac{1}{2}$ với tâm là trực tâm của tam giác đó.
Định lý 3. (Định lý Fontene thứ hai, định lý Griffith). Cho tam giác $ABC$ với tâm đường tròn ngoại tiếp $O$ và một điểm $P$ khác $O$. Khi đó đường tròn ngoại tiếp tam giác pedal của $P$ với tam giác $ABC$ đi qua cực trực giao của $OP$ với tam giác $ABC$ (điểm này cũng thuộc đường tròn chín điểm của tam giác $ABC$ và là điểm Anti-Steiner của đường thẳng $OP$ với tam giác có ba đỉnh là trung điểm ba cạnh của tam giác $ABC$).
Định lý 3 khẳng định rằng $T$ thuộc đường tròn chín điểm của tam giác $ABC$ và đường tròn ngoại tiếp của tam giác $P_{a}P_{b}P_{c}$.
Định lý 4. (sử dụng kí hiệu của bài toán trên) $A'$ là trung điểm của đoạn thẳng $BC$. Khi đó hai tam giác $APO$ và $TP_{a}A'$ đồng dạng cùng hướng.
Gợi ý chứng minh Định lý 4. Nếu hai đường thẳng $OP$ và $BC$ cắt nhau thì tâm của phép đồng dạng thuận biến tam giác $APO$ thành tam giác $TP_{a}A'$ là giao điểm của hai đường thẳng $OP$ và $BC$ (hãy sử dụng chứng minh của định lý Fontene thứ nhát). Ngược lại, nếu hai đường thẳng này song song thì tam giác $APO$ là ảnh của tam giác $TP_{a}A'$ qua một phép tịnh tiến.
Quay lại với bài toán. Mình kí hiệu $N$ là tâm đường tròn chín điểm của tam giác $ABC$, $AA_{1}$ là đường kính của đường tròn ngoại tiếp tam giác $ABC$, và $A'$, $B'$, $C'$ là trung điểm của các đoạn thẳng $BC$, $CA$, $AB$. Mình sẽ chứng minh $(TA'_{p}, TA')\equiv (TP_{a}, TA')\pmod{\pi}$. Biến đổi góc định hướng dưới đây có thể chưa phải là gọn nhất.
Lưu ý rằng các điểm $T$, $A'$, $B'$, $C'$, $A'_{p}$ thuộc đường tròn chín điểm của tam giác $ABC$.
\[ (TA'_{p}, TA') \equiv \frac{1}{2}(\overrightarrow{NA'_{p}}, \overrightarrow{NA'}) \pmod{\pi} \text{(góc ở tâm và góc nội tiếp cùng chắn một cung)} \]
Theo Định lý 2 thì
\[ \frac{1}{2}(\overrightarrow{NA'_{p}}, \overrightarrow{NA'}) \equiv \frac{1}{2}(\overrightarrow{OA_{p}}, \overrightarrow{OA_{1}}) \pmod{\pi} \]
Góc ở tâm có số đo gấp đôi góc nội tiếp cùng chắn một cung (định lý góc nội tiếp), do đó
\[ \frac{1}{2}(\overrightarrow{OA_{p}}, \overrightarrow{OA_{1}}) \equiv (AA_{p}, AA_{1}) \equiv (AP, AO) \pmod{\pi} \]
Như vậy
\[ (TA'_{p}, TA') \equiv (AP, AO) \pmod{\pi} \]
Theo Định lý 4, $(TP_{a}, TA') \equiv (AP, AO) \pmod{\pi}$.
Do đó $(TP_{a}, TA') \equiv (TA'_{p}, TA')\pmod{\pi}$, kéo theo $(TP_{a}, TA'_{p})\equiv 0 \pmod{\pi}$.
Điều này nghĩa là $T, P_{a}, A'_{p}$ thẳng hàng. $\blacksquare$
Bài viết đã được chỉnh sửa nội dung bởi QuangDuong1201: 18-09-2023 - 19:40