Chủ đề này có 4 trả lời

[DaiphongLT]

Cho $\Delta ABC$ nội tiếp đường tròn $(O). O_a, O_b, O_c$ lần lượt là tâm của $(OBC), (OCA), (OAB). XYZ$ là tam giác Cevian của $O$ đối với $\Delta O_aO_bO_c. P$ là trực tâm $\Delta XYZ.$ Chứng minh $OP$ đi qua điểm Kosnita của $\Delta ABC.$  
Định nghĩa điểm Kosnita: https://vi.wikipedia...Định_lý_Kosnita

[DaiphongLT]

Lời giải:
Bổ đề 1: Cho tam giác $ABC, P$ bất kì. Đường thẳng qua $P$ vuông góc $PA,PB,PC$ cắt $BC, CA, AB$ tại $X,Y,Z.$ Khi đó $X, Y, Z$ thẳng hàng (Bổ đề khá quen thuộc)
Bổ đề 2: Cho $\Delta ABC$ và $\Delta XYZ.$ Khi đó các đường thẳng lần lượt qua $X$ vuông góc $BC,$ qua $Y$ vuông góc $CA,$ qua $Z$ vuông góc $AB$ đồng quy khi và chỉ khi các đường thẳng qua $A$ vuông góc $YZ,$ qua $B$ vuông góc $ZX,$ qua $C$ vuông góc $XY$ đồng quy (Hệ quả trực tiếp của định lí Carnot)
Gọi $K$ là điểm Kosnita của $\Delta ABC. D, E, F$ là hình chiếu của $K$ lên $BC,CA,AB. H$ là trực tâm $\Delta DEF, N$ là tâm Euler của $\Delta ABC$
$O'$ đối xứng với $O$ qua $BC,$ $A_a$ là tâm $(AOO').$ Định nghĩa $B_b, C_c$ tương tự, khi đó ta dễ thấy $\widehat{ANA_a}=90^{\circ}$ nên theo bổ đề 1 suy ra $\overline{A_a, B_b, C_c}$
Xét $I_{O}^{R^2}:(A_a)\leftrightarrow AO_a,$ để ý rằng $AO_a, BO_b, CO_c$ đồng quy tại $K$ do đó các đường tròn $(A_a), (B_b), (C_c)$ đồng trục với trục đẳng phương là $OK$ nên $\overline{A_a, B_b, C_c}\perp OK$
Áp dụng bổ đề 2 và hai tam giác $KEF$ và $NC_cB_b$ khi đó ta cũng có được $KH\perp \overline{A_a, B_b, C_c}$
Từ đây ta suy ra $\overline{O,K,H}$
Dễ chứng minh được 2 tam giác $DEF$ và $XYZ$ vị tự với nhau, do đó $OP$ đi qua $H$
Kết hợp hai kết quả trên, ta suy ra điều phải chứng minh
P/s: Lời giải của mình chưa được chỉnh chu, thiên về phần gợi ý khá nhiều, có một số kết quả chứng minh cũng khá dài, khi nào có thời gian mình sẽ hoàn thiện lời giải bài toán này sau
Một kết quả khác cũng rất hay là $\overline{HO}=3\overline{HK}$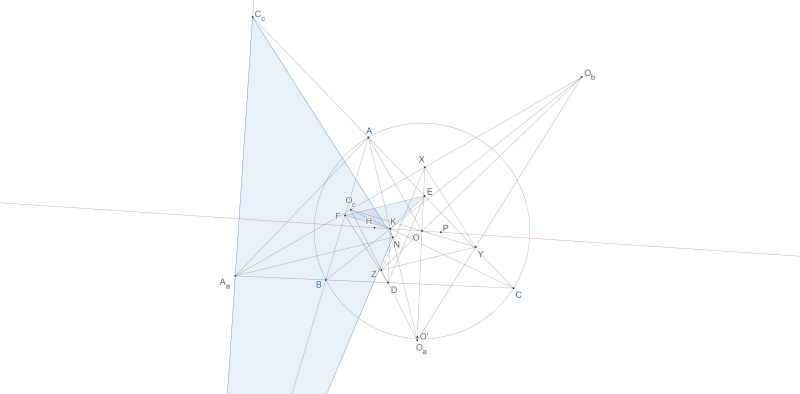

Bài viết đã được chỉnh sửa nội dung bởi DaiphongLT: 27-10-2023 - 07:19

[DaiphongLT]

Tiếp tục về mô hình này, mình có phát hiện được 2 bài toán sau:
Bài 2: Cho tam giác $ABC$ nội tiếp đường tròn $(O), K$ là điểm Kosnita của tam giác $ABC. X, Y, Z$ lần lượt đối xứng với $K$ qua $BC, CA, AB.$ Gọi $H$ là trực tâm $\Delta XYZ.$ Chứng minh $KO=KH$
Bài 3: Cho tam giác $ABC$ nội tiếp đường tròn $(O),$ trực tâm $H, K$ là điểm Kosnita của tam giác $ABC. X$ là giao điểm của $AH$ với $(O), BK, CK$ lần lượt cắt $(BHC)$ tại $Y, Z. BX, CX$ lần lượt cắt $(BHC)$ tại $U, V.$ Chứng minh $YZ, BC, UV$ đồng quy
Bài 4 (Sưu tầm): Cho tam giác $ABC$ nội tiếp đường tròn $(O),$ các đường phân giác $AD,BE,CF$ đồng quy tại $I.$ Chứng minh $OI$ đi qua tâm Euler của tam giác $DEF$
 

Bài viết đã được chỉnh sửa nội dung bởi DaiphongLT: 29-10-2023 - 06:17

[MinhAnhNguyen]

Cho $\Delta ABC$ nội tiếp đường tròn $(O). O_a, O_b, O_c$ lần lượt là tâm của $(OBC), (OCA), (OAB). XYZ$ là tam giác Cevian của $O$ đối với $\Delta O_aO_bO_c. P$ là trực tâm $\Delta XYZ.$ Chứng minh $OP$ đi qua điểm Kosnita của $\Delta ABC.$  
Định nghĩa điểm Kosnita: https://vi.wikipedia...Định_lý_Kosnita

Ta đưa về mô hình tâm nội tiếp bởi vì $O_aO$ là phân giác góc $\angle O_bO_aO_c$

Đưa về bài toán sau:

Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. $AI,BI,CI$ giao $BC,AC,AB$ tại $X,Y,Z$. $G$ là trực tâm của $\Delta XYZ$. $O_a,O_b,O_c$ là điểm đối xứng của $I$ qua $BC,AC,AB$. Chứng minh $IG$ đi qua điểm đồng quy của $AO_a,BO_b,CO_c$

 

Bổ đề: Cho $\Delta ABC$, điểm $P$ bất kỳ trong mặt phẳng. $AP,BP,CP$ giao $BC,AC,AB$ tại $D,E,F$. $Q$ bất kỳ trên mặt phẳng. $DQ,EQ,FQ$ giao $EF,FD,DE$ tại $D_1,E_1,F_1$. $PD_1,PE_1,PF_1$ giao $BC,AC,AB$ tại $A_1,B_1,C_1$. Chứng minh rằng $AA_1,BB_1,CC_1$ đồng quy trên $PQ$

 

Chứng minh:

Gọi các điểm như hình vẽ

Ta có $F(PI,AJ)=F(PX,C_1B_1)=P(FX,C_1B_1)=P(FX,YZ)$

Mà $F(PI,AJ)=F(CE,AB_1)=F(EC,B_1A)=P(EF,E_1D)=E(PF,E_1D)=E(PF,YF_1)=F(PE,YF_1)=F(PX,YZ$

Nên $X,Y,Z$ thẳng hàng

Dùng Desargue cho $\Delta QEF$ và $\Delta PC_1B_1$ nên $P,Q,G$ thẳng hàng

Áp dụng định lý Pappus cho bộ $(B,C_1,F)$ và bộ $(C,B_1,E)$ nên $P,H,G$ thẳng hàng

Suy ra $H,P,Q$ thẳng hàng

DPCM

 

 

Quay lại bài toán

Gọi $A_1,A_2,G_x$ là giao của $AO_a,AX,XG$ và $BC,YZ,YZ$

Theo hàng điểm có $YZ$ là phân giác $\angle AG_xI$

Và $A_1A_2$ vuông góc $BC$

Nên $\angle A_2G_xA_1=\angle A_2XA_1=\angle AG_xA_2=\angle A_2G_xI$

Nên $A_1,G_x,I$ thẳng hàng

Áp dụng bổ đề có dpcm

[DaiphongLT]

Ta đưa về mô hình tâm nội tiếp bởi vì $O_aO$ là phân giác góc $\angle O_bO_aO_c$

Đưa về bài toán sau:

Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. $AI,BI,CI$ giao $BC,AC,AB$ tại $X,Y,Z$. $G$ là trực tâm của $\Delta XYZ$. $O_a,O_b,O_c$ là điểm đối xứng của $I$ qua $BC,AC,AB$. Chứng minh $IG$ đi qua điểm đồng quy của $AO_a,BO_b,CO_c$

 

Bổ đề: Cho $\Delta ABC$, điểm $P$ bất kỳ trong mặt phẳng. $AP,BP,CP$ giao $BC,AC,AB$ tại $D,E,F$. $Q$ bất kỳ trên mặt phẳng. $DQ,EQ,FQ$ giao $EF,FD,DE$ tại $D_1,E_1,F_1$. $PD_1,PE_1,PF_1$ giao $BC,AC,AB$ tại $A_1,B_1,C_1$. Chứng minh rằng $AA_1,BB_1,CC_1$ đồng quy trên $PQ$

 

Chứng minh:

Gọi các điểm như hình vẽ

Ta có $F(PI,AJ)=F(PX,C_1B_1)=P(FX,C_1B_1)=P(FX,YZ)$

Mà $F(PI,AJ)=F(CE,AB_1)=F(EC,B_1A)=P(EF,E_1D)=E(PF,E_1D)=E(PF,YF_1)=F(PE,YF_1)=F(PX,YZ$

Nên $X,Y,Z$ thẳng hàng

Dùng Desargue cho $\Delta QEF$ và $\Delta PC_1B_1$ nên $P,Q,G$ thẳng hàng

Áp dụng định lý Pappus cho bộ $(B,C_1,F)$ và bộ $(C,B_1,E)$ nên $P,H,G$ thẳng hàng

Suy ra $H,P,Q$ thẳng hàng

DPCM

368114034_1069878864427730_7888921593160612058_n.png

 

 

Quay lại bài toán

Gọi $A_1,A_2,G_x$ là giao của $AO_a,AX,XG$ và $BC,YZ,YZ$

Theo hàng điểm có $YZ$ là phân giác $\angle AG_xI$

Và $A_1A_2$ vuông góc $BC$

Nên $\angle A_2G_xA_1=\angle A_2XA_1=\angle AG_xA_2=\angle A_2G_xI$

Nên $A_1,G_x,I$ thẳng hàng

Áp dụng bổ đề có dpcm

Screenshot 2023-10-29 022104.png

Lời giải ngắn gọn thật  , mình đã biết trước một số kết quả nên cách làm không tự nhiên lắm