
Come in!
Bắt đầu bởi white1409, 19-10-2006 - 10:00
#1
 Đã gửi 19-10-2006 - 10:00
Đã gửi 19-10-2006 - 10:00

Cho  ABC có M,N,P là trung điểm các cạnh BC,CA,AB.Gọi X là 1 điểm bên ngoài
ABC có M,N,P là trung điểm các cạnh BC,CA,AB.Gọi X là 1 điểm bên ngoài  .C/m diện tích 1 trong các
.C/m diện tích 1 trong các  XAM,XBN,XCP=tổng diện tích 2
XAM,XBN,XCP=tổng diện tích 2  còn lại
còn lại
The Last Leaf
NMT
NMT
#2
 Đã gửi 28-10-2006 - 11:08
Đã gửi 28-10-2006 - 11:08

Các bạn thử lấy điểm Y:G trung điểm XY(G là trọng tâm tam giác ABC) xem có được không?
The Last Leaf
NMT
NMT
#3
 Đã gửi 11-11-2006 - 10:58
Đã gửi 11-11-2006 - 10:58

Tớ còn 1 bài nữa này
Cho hình bình hành ABCD và 1 điểm P nằm trong hình.Qua P kẻ KM song song
BC(K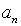 AB,M
AB,M  CD).Qua P kẻ LN song song AB(L
CD).Qua P kẻ LN song song AB(L  BC,N
BC,N  AD).Gọi Q là giao các đoạn thẳng nối các tđiểm của tứ giác KLMN,S là giao 2 đường chéo hình bình hành ABCD.C/m P,Q,S thẳng hàng.
AD).Gọi Q là giao các đoạn thẳng nối các tđiểm của tứ giác KLMN,S là giao 2 đường chéo hình bình hành ABCD.C/m P,Q,S thẳng hàng.
Cho tớ hỏi đánh kí hiệu song song làm thế nào vậy?
Cho hình bình hành ABCD và 1 điểm P nằm trong hình.Qua P kẻ KM song song
BC(K
Cho tớ hỏi đánh kí hiệu song song làm thế nào vậy?
The Last Leaf
NMT
NMT
#4
 Đã gửi 25-02-2007 - 12:24
Đã gửi 25-02-2007 - 12:24

Bài này ko cần phải có đk $X$ ở ngoàiCho
ABC có M,N,P là trung điểm các cạnh BC,CA,AB.Gọi X là 1 điểm bên ngoài
.C/m diện tích 1 trong các
XAM,XBN,XCP=tổng diện tích 2
còn lại
Gọi $G$ là trọng tâm
Ta sẽ CM $S(XCP)=S(XAM)+S(XBN)$. Thật vậy:
$S(XCP)=S(XAM)+S(XBN)$
$\Leftrightarrow \dfrac{1}{3}S(XCP)= \dfrac{1}{3}S(XAM)+ \dfrac{1}{3}S(XBN)$
$\Leftrightarrow S(XGP)=S(XGM)+S(XGN)$ (1)
Nối $MN \cap PC \equiv R$. Hạ đường cao $PP', MM', NN', RR'$ xuống $GX$.
$\Rightarrow (1) \Leftrightarrow PP'=MM'+NN'$
Dễ có $R$ là tđ $PC$ và $PC=3PG \Rightarrow PG=2GR$
Kẻ đường TB $IK$ của $\delta GPP' \Rightarrow RR'=IK= \dfrac{1}{2}PP'$
Mặt khác, $R$ tđ $MN \Rightarrow 2RR'=MM'+NN'=PP'$
$\Rightarrow$ đpcm
Bài viết đã được chỉnh sửa nội dung bởi tunganh: 25-02-2007 - 12:26
But only love can say-try again or walk away...But I believe for you and me...The sun will shine one day...So I'll just play my part...And pray you'll have a change of heart...But I can't make you see it through...That's something only love can do
Diễn đàn toán thpt: http://toanthpt.net/forum
Toán THCS: http://www.toanthpt....isplay.php?f=13
Diễn đàn toán thpt: http://toanthpt.net/forum
Toán THCS: http://www.toanthpt....isplay.php?f=13
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh



