Tiep tuc, cau hoi lon´ nhat duoc dat ra o day la` : Ca^u´ truc´
http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} cua K-local spin bordism theory la` gi`. Noi´ chung theo nhu tu tuong' lon´ lao cua Whitehead, nguoi` ta co^´ gang´ xay dung cac´ topological spaces tren cac´ cell cua no´, nen vi` the´ nguoi` ta nhan thay o day viec nghien cuu´ multiplicative splitting spin bordism tre^n cac´
http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} la` co´ y´ nghia.
Gioi´ thieu chut´ so qua ve splitting spin bordism: Noi´ chung ly´ thuyet duoc xay dung chu' yeu boi Brown, Peterson, Anderson voi´ Morava K-theory noi' tieng´. Co´ 1 dieu nen biet rang 2 spin manifolds duoc goi la spin bordant neu va chi' neu tat ca cac´ Stiefel-Whitney class va` KO-Characteristic number coincide.
Hon nua cac´ Spin Manifold duoc tinh´ toan´ cu the^' nhu sau:
Mspin
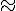 http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Lambda_{i=1}^{\infty} http://dientuvietnam...etex.cgi?TS^{0}
http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Lambda_{i=1}^{\infty} http://dientuvietnam...etex.cgi?TS^{0}Voi´
http://dientuvietnam.net/cgi-bin/mimetex.cgi?\zeta la` generator cua nhom´ 1st-homotopy cua' K(1)-local sphere.
http://dientuvietnam.net/cgi-bin/mimetex.cgi?T_{\zeta} la`
http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty}-cone over
http://dientuvietnam.net/cgi-bin/mimetex.cgi?\zeta Ket qua chinh´ cua Splitting formula la`:

* Mspin
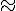

*KO
http://dientuvietnam.net/cgi-bin/mimetex.cgi?\otimes http://dientuvietnam...n/mimetex.cgi?T { http://dientuvietnam.net/cgi-bin/mimetex.cgi?f_{1}, http://dientuvietnam.net/cgi-bin/mimetex.cgi?f_{2},...}.
Cai´ homotpy cua' Mspin nay` la` 1 http://dientuvietnam.net/cgi-bin/mimetex.cgi?\theta-algebra over

*KO. 1 dang phat´ bieu khac´ cua no´ la`
Mspin*X http://dientuvietnam.net/cgi-bin/mimetex.cgi?\otimes_{Mspin*X} KO*
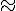
KO*X. Cai´ nay` duoc goi la conner-floyd isomorphism. Den day thi` nguoi` ta duong` nhu hieu hieu doi chut´ ve` elliptic cohomology, mo^i´ lien quan cua' Adams spectral sequences + stable homotopy + topological modular form.
Hopkin da cm rang` viec xay dung 1 Witten orientation duoc rut´ gon ve^` bai` toan´ tim` topological modular form cua K(1) va` K(2).
Voi´ K(n) la` Morava K-theory tai prime 2. To´ viet topological modular form ngan´ gon la` http://dientuvietnam.net/cgi-bin/mimetex.cgi?tmf
Cai´ Conner-Floyd isomorphism o tren duoc viet lai duoi´ dang sau:
http://dientuvietnam.net/cgi-bin/mimetex.cgi?MO<8>*X http://dientuvietnam.net/cgi-bin/mimetex.cgi?\otimes_{MO<8>*X} http://dientuvietnam.net/cgi-bin/mimetex.cgi?tmf*
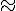
http://dientuvietnam.net/cgi-bin/mimetex.cgi?tmf*X.
trong K(1)-local category.
Noi´ doi chut´ ve^` http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty}-spectra va` localization:
Goi http://dientuvietnam.net/cgi-bin/mimetex.cgi?T la` Category cua cac´ topological space ( y´ noi´ weak topology) va` http://dientuvietnam.net/cgi-bin/mimetex.cgi?T* la` basis cua no´. Goi U la` real inner product space huu han chieu` , 1 prespectrum X la` 1 ho cua' cac´ pointed spaces http://dientuvietnam.net/cgi-bin/mimetex.cgi?X_{V} duoc danh´ so^´ boi cac´ khong gian con huu han chieu V

U tuong ung´ voi´ maps:
http://dientuvietnam.net/cgi-bin/mimetex.cgi?S^{W-V} ^ http://dientuvietnam.net/cgi-bin/mimetex.cgi?X_{V} --->http://dientuvietnam.net/cgi-bin/mimetex.cgi?X_{V}.
voi´

V

W.
1 spectrum la` 1 prespectrum voi´ tinh´ chat^´ co^ng. sao cho maps sau la` 1 homemorphisms:
http://dientuvietnam.net/cgi-bin/mimetex.cgi?t_{W,V}: http://dientuvietnam.net/cgi-bin/mimetex.cgi?X_{V} ---> http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Omega^{W-V} (http://dientuvietnam.net/cgi-bin/mimetex.cgi?X_{V})
1 operad trong 1 symmetric monoid category M = (M,I,http://dientuvietnam.net/cgi-bin/mimetex.cgi?\otimes) la` 1 ho cac´ objects http://dientuvietnam.net/cgi-bin/mimetex.cgi?T_{0}, http://dientuvietnam.net/cgi-bin/mimetex.cgi?T_{1},......
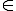
M voi´ 1 right http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Sigma_{n} action tren mo^i http://dientuvietnam.net/cgi-bin/mimetex.cgi?T_{n} va` 1 http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Sigma_{n} x http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Sigma_{i_{1}} x ... x http://dientuvietnam.net/cgi-bin/mimetex.cgi?\Sigma_{i_{n}}- equivariant structure map:
http://dientuvietnam.net/cgi-bin/mimetex.cgi?X^{(n)} ---> X, duoi´ isometry p(f): http://dientuvietnam.net/cgi-bin/mimetex.cgi?U^{(n)} ---> U.
1 operad http://dientuvietnam.net/cgi-bin/mimetex.cgi?T over L la` 1 http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} ne^u´ voi´ moi space contractible va` 1 nhom´ free tac´ dong trong 1 free fashion
1 http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} ring spectrum la` 1 spectrum X cung` voi´ 1 map http://dientuvietnam.net/cgi-bin/mimetex.cgi?T --> End(X) cua cac´ pointed operad over L.
co´ the lay vi´ du truc quan: 1 sphere spectrum la` 1 http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} spectrum.
----------
Ps: Thuc ra cai´ spectrum to´ noi´ o day cung chinh´ la` cai´ spectrum o' bai` tren to´ da ban` luan, chi' co´ dieu o day duoc mo rong ra cho http://dientuvietnam.net/cgi-bin/mimetex.cgi?E_{\infty} ma` thoi
Nhac´ de^n´ Witten la` tuc´ la` noi´ den^´ String theory ro^i` da^y´, anh Math0
Bài viết đã được chỉnh sửa nội dung bởi quantum-cohomology: 07-03-2005 - 20:03







