Mình chả thấy ai quy ước $0^0=1$ cả, mình chỉ thấy qui ước $0^0$ vô nghĩa thôi. Trong SGK Toán qui ước $0^0$ vô nghĩa mà, với lại bấm máy tính thì $0^0$ nó ra "Math Error"Có lẽ là như thế này
$lim_{a -> 0} a^{0} = lim_{a -> 0} 1 =1$
Cái này em làm bừa
sai sót chỗ nào mong mọi người bỏ qua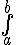
Nói chung người ta qui ước $0^0=1$ ( thế mà trước đây em lại cho nó là vô nghĩa)

không mũ không
#21
 Đã gửi 24-08-2007 - 21:37
Đã gửi 24-08-2007 - 21:37

#22
 Đã gửi 25-08-2007 - 11:43
Đã gửi 25-08-2007 - 11:43

Mình chả thấy ai quy ước cả, mình chỉ thấy qui ước vô nghĩa thôi. Trong SGK Toán qui ước vô nghĩa mà, với lại bấm máy tính thì nó ra "Math Error"
0^0 = 1 , dòng thứ 7 trang 11 giáo trình toán giải tích tập 2 của J.Monier , NXBGD do Ng~ Văn Thường dich , in xong và nộp lưu chiểu tháng 4 năm 2001
#23
 Đã gửi 25-08-2007 - 12:25
Đã gửi 25-08-2007 - 12:25

Bài viết đã được chỉnh sửa nội dung bởi nguyendinh_kstn_dhxd: 25-08-2007 - 12:26
#24
 Đã gửi 25-08-2007 - 17:18
Đã gửi 25-08-2007 - 17:18

0^a = 0 với a#0 , a^0 = 1 với a#0 , nó giống như cái máy tính có thể làm đc mọi thứ trừ treo máy , khi 2 cái gặp nhau thì phải có cách # , 0^0 ko tồn tại thông thg` giống như ko tồn tại mâu thuẫn trong toán học , tuy nhiên khi đưa ra đn 1 cái j` thì ng` ta thg` nghĩ tới ứng dụng của nó , và các biểu thức thì ứng dụng chính là vào các phép biến đổi cho thuận tiện nhất , Chẳng hạn qui ước 0! = 1 sẽ dễ dàng cho viết công thức Taylor chẳng hạn , thì ng` ta mới qui ước 0!=1 . Các bạn tìm 0^0 có lẽ nên chú ý tới các ứng dụng của nó vào các phép biến đổi thì hơn , còn c/m nó là bao nhiêu đó là 1 việc vô ích , bởi thích cho nó là bao nhiêu cũng đc
0^0 = 1 , dòng thứ 7 trang 11 giáo trình toán giải tích tập 2 của J.Monier , NXBGD do Ng~ Văn Thường dich , in xong và nộp lưu chiểu tháng 4 năm 2001
Nhân tiện nhắc đến chuỗi Taylor
Anh có biết ở tài liệu nào có ghi chứng minh cho chuỗi Taylor không ạ
THAnKS
#25
 Đã gửi 25-08-2007 - 18:41
Đã gửi 25-08-2007 - 18:41

2
C/m cho chuỗi Taylor , câu này ko rõ ý , bạn có ý đinh jhoc toán caoccap thì nên học từ đầuNhân tiện nhắc đến chuỗi Taylor
Anh có biết ở tài liệu nào có ghi chứng minh cho chuỗi Taylor không ạ
THAnKS
#26
 Đã gửi 26-08-2007 - 02:48
Đã gửi 26-08-2007 - 02:48

#27
 Đã gửi 26-08-2007 - 10:38
Đã gửi 26-08-2007 - 10:38

Bài viết đã được chỉnh sửa nội dung bởi Niels Henrik Abel: 26-08-2007 - 13:09
#28
 Đã gửi 17-11-2007 - 03:36
Đã gửi 17-11-2007 - 03:36

theo tớ, đây là phương pháp "tạm gọi" rõ ràng nhất để có thể qui ước $0^0 = 1$SGK cấp 3 dậy cái này kỹ rồi mà, chắc tại bạn gì ko chịu học kỹ. cm $0^0 = 1$ có thể làm bằng 1 cách thiếu chính xác và nông dân như sau, ta có $lim_{x \rightarrow 0} x^x = lim_{x \rightarrow 0} e^{x.logx} = lim_{x \rightarrow 0}e^{\dfrac{logx}{1/x}} = lim_{x \rightarrow 0} e^{\dfrac{1/x}{-1/x^2}} = lim_{x \rightarrow 0} e^0 = 1$.
Vấn đề giá trị của $0^0 $ thì mình không biết có qui ước chung quốc tế không nhưng trong sách của Pháp thì qui ước =1 và mấy ông thầy dạy toán ở đây cũng khẳng định như vậy
Bài viết đã được chỉnh sửa nội dung bởi T*genie*: 17-11-2007 - 03:38
#29
 Đã gửi 05-12-2007 - 18:24
Đã gửi 05-12-2007 - 18:24

Không cần qui ước gì hếttheo tớ, đây là phương pháp "tạm gọi" rõ ràng nhất để có thể qui ước $0^0 = 1$
Vấn đề giá trị của $0^0 $ thì mình không biết có qui ước chung quốc tế không nhưng trong sách của Pháp thì qui ước =1 và mấy ông thầy dạy toán ở đây cũng khẳng định như vậy.
nó =1 đấy !
Vì sao ????
Đời người là một hành trình...
#30
 Đã gửi 05-12-2007 - 18:28
Đã gửi 05-12-2007 - 18:28

Bạn đã biết đến Lôpitan chưa: thì bạn hãy xem bài này :
Tính giới hạn dạng vô định nhé
$\lim_{x\to a} {f(x)}^{g(x)}$ ( vô định nhé ,và số a thuộc tập số thực mờ rộng)
KHi ấy : ta chấp nhận : ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$ cài này không ?
Tiếp tục áp dụng Lôpitan cho: $g(x)\ln{f(x)}=\dfrac{u(x)}{v(x)}$
Chuyện dùng Lôpitan là một chuỗi dài kỉ niệm của mình
Nhưng cái quan trọng... THPT dùng được hay không còn tuỳ thuộc mỗi người
Cho dùng Lôpitan không thì không cân biết đến!
Ở đây họ đã công nhận một điều hơn thề!
Công nhận một điều dính líu bên GT phức, ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$
$f(x)>0$ ( không ?) công nhận :$\ln{\sqrt{-1}}=\ln{i}$
Quá lắm...!
NHưng GT1 đã góp phần cm lại toán bộ những điều đã công nhận ,
CM chứ không dùng " dễ thấy ta có nhé các bạn"
Chúc bạn vui !
Đấy
Liên quan hàm biên` phức đấy
Đời người là một hành trình...
#31
 Đã gửi 05-12-2007 - 22:40
Đã gửi 05-12-2007 - 22:40

Mình hỏi bạn cái này ,bạn đả sử dùng những điều chưa học chưa?
Bạn đã biết đến Lôpitan chưa: thì bạn hãy xem bài này :
Tính giới hạn dạng vô định nhé
$\lim_{x\to a} {f(x)}^{g(x)}$ ( vô định nhé ,và số a thuộc tập số thực mờ rộng)
KHi ấy : ta chấp nhận : ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$ cài này không ?
Tiếp tục áp dụng Lôpitan cho: $g(x)\ln{f(x)}=\dfrac{u(x)}{v(x)}$
Chuyện dùng Lôpitan là một chuỗi dài kỉ niệm của mình
Nhưng cái quan trọng... THPT dùng được hay không còn tuỳ thuộc mỗi người
Cho dùng Lôpitan không thì không cân biết đến!
Ở đây họ đã công nhận một điều hơn thề!
Công nhận một điều dính líu bên GT phức, ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$
$f(x)>0$ ( không ?) công nhận :$\ln{\sqrt{-1}}=\ln{i}$
Quá lắm...!
NHưng GT1 đã góp phần cm lại toán bộ những điều đã công nhận ,
CM chứ không dùng " dễ thấy ta có nhé các bạn"
Chúc bạn vui !
Đấy
Liên quan hàm biên` phức đấy
VÀ nó chứa đựng nhiều mâu thuẩn
tôi chả hiểu j` cả. chả liên quan j`.
à mà nhân tiện.việc SGK công nhận cũng lả bt . chả ai đi dạy giải tích phức cho học sinh đại trà thpt cả. ng` ta chứng minh cũng đc. nhưng mà cm xong thì ko ai hiểu.nói như bạn năm lớp 5.6 học số tự nhiên hay chia hết cũng lôi trường. vành với cả định nghĩa phép toán.lớp tương đương vào thì chắc là cũng vui lắm.
#32
 Đã gửi 13-12-2007 - 02:27
Đã gửi 13-12-2007 - 02:27

Mình hỏi bạn cái này ,bạn đả sử dùng những điều chưa học chưa?
Bạn đã biết đến Lôpitan chưa: thì bạn hãy xem bài này :
Tính giới hạn dạng vô định nhé
$\lim_{x\to a} {f(x)}^{g(x)}$ ( vô định nhé ,và số a thuộc tập số thực mờ rộng)
KHi ấy : ta chấp nhận : ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$ cài này không ?
Tiếp tục áp dụng Lôpitan cho: $g(x)\ln{f(x)}=\dfrac{u(x)}{v(x)}$
Chuyện dùng Lôpitan là một chuỗi dài kỉ niệm của mình
Nhưng cái quan trọng... THPT dùng được hay không còn tuỳ thuộc mỗi người
Cho dùng Lôpitan không thì không cân biết đến!
Ở đây họ đã công nhận một điều hơn thề!
Công nhận một điều dính líu bên GT phức, ${f(x)}^{g(x)}=e^{g(x)\ln{f(x)}}$
$f(x)>0$ ( không ?) công nhận :$\ln{\sqrt{-1}}=\ln{i}$
Quá lắm...!
NHưng GT1 đã góp phần cm lại toán bộ những điều đã công nhận ,
CM chứ không dùng " dễ thấy ta có nhé các bạn"
xin lỗi nhưng tớ chả thấy gì liên quan đến vấn đề thảo luận!
#33
 Đã gửi 13-12-2007 - 16:44
Đã gửi 13-12-2007 - 16:44

Rõ ràng ta có x^0=1 và 0^x=0 với mọi x. Nếu xét x=0 thì không lẽ (x^0)=(0^x). Vô lý.
Ai cũng biết x^0=1 và 0^x=0 đều không xét đến x=0 vì 0^0 là không xác định.
#34
 Đã gửi 14-12-2007 - 18:34
Đã gửi 14-12-2007 - 18:34

Anh class tự mâu thuẫn rồiAi nói 0^0=1 hay 0^0=0 thì học lại là vừa.
Rõ ràng ta có x^0=1 và 0^x=0 với mọi x. Nếu xét x=0 thì không lẽ (x^0)=(0^x). Vô lý.
Ai cũng biết x^0=1 và 0^x=0 đều không xét đến x=0 vì 0^0 là không xác định.
dòng trên nói là "với mọi x" còn dòng dưới là "không xét x=0"
Nếu như "x^0=1 và 0^x=0 với mọi x" là mệnh đề đúng thì mệnh đề kéo theo của nó là x^0=0^
do đó mệnh đề "x^0=1 và 0^x=0 với mọi x" là sai; vì vậy không thể "cho x=0" được
#35
 Đã gửi 01-01-2008 - 20:08
Đã gửi 01-01-2008 - 20:08

anh classpad300 nóng thế, mọi người chỉ đang thảo luận về $ 0^{0} $ thôi chứ có ai "dám" khẳng định bằng mấy đâuAi nói 0^0=1 hay 0^0=0 thì học lại là vừa.
Rõ ràng ta có x^0=1 và 0^x=0 với mọi x. Nếu xét x=0 thì không lẽ (x^0)=(0^x). Vô lý.
Ai cũng biết x^0=1 và 0^x=0 đều không xét đến x=0 vì 0^0 là không xác định.
x^0=1 và 0^x=0 với mọi x với mọi x ở đây là
Bài viết đã được chỉnh sửa nội dung bởi T*genie*: 01-01-2008 - 20:09
#36
 Đã gửi 03-01-2008 - 23:52
Đã gửi 03-01-2008 - 23:52

Thế 0^0 = 0 x 0 = 1 (mọi số lũy thừa không thì = 1)
Thế các ku lại nghĩ xem 2 x 0 = 0 => mọi số nhân với 0 thì bằng 0 => nó chơi nhau rồi!!!!! Kíu!! Điên mất
TRẺ KHÔNG XÔNG PHA, GIÀ SINH HƯ
#37
 Đã gửi 04-01-2008 - 00:42
Đã gửi 04-01-2008 - 00:42

em học lớp không cao lắm nên vẫn chưa học nhiều về lũy thừa nhưng
0 x 0 = 0 mũ 2 chứ
#38
 Đã gửi 06-02-2008 - 13:22
Đã gửi 06-02-2008 - 13:22

#39
 Đã gửi 12-08-2009 - 16:14
Đã gửi 12-08-2009 - 16:14

~~--**Diễn Đàn Toán học**--~~
",,..--~~Thế giới để ước mơ toán học bay xa~~--..,,"
#40
 Đã gửi 12-08-2009 - 16:37
Đã gửi 12-08-2009 - 16:37

Anh bấm máy tính 0^0 ra Math ERROR nàyTheo sách giáo khoa là chắc nhất theo em thi 0^0 phải bằng 0 thôi!
Nếu một ngày bạn cảm thấy buồn và muốn khóc,hãy gọi cho tôi nhé.
Tôi không hứa sẽ làm cho bạn cười nhưng có thể tôi sẽ khóc cùng với bạn.
Nếu một ngày bạn muốn chạy chốn tất cả hãy gọi cho tôi.
Tôi không yêu cầu bạn dừng lại nhưng tôi sẽ chạy cùng với bạn.
Và nếu một ngày nào đó bạn không muốn nghe ai nói nữa,hãy gọi cho tôi nhé.
Tôi sẽ đến bên bạn và chỉ im lặng.
Nhưng nếu một ngày bạn gọi đến tôi mà không thấy tôi hồi âm...
Hãy chạy thật nhanh đến bên tôi vì lúc đó tôi mới là người cần bạn.
________________________________________________________
Vu Thanh Tu, University of Engineering & Technology
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh








