Edited by leecom, 02-01-2007 - 08:17.
#1
Posted 02-01-2007 - 08:15
leecom
-
- Thành viên
-
- 327 posts
Sĩ quan
Cho $k$ số nguyên dương $a_{1},a_{2},...,a_{k}$ thỏa mãn $1\le a_{1}<a_{2}<...<a_{k}\le n$ sao cho $[a_{i},a_{j}]>n$ với mọi $1\le i\le j\le n$. Chứng minh rằng $\sum\limits_{i=1}^{k} \dfrac{1}{a_{i}}<\dfrac{3}{2}$
The Past, The Present, and The Future...
#2
Posted 08-01-2007 - 13:45
tanlsth
-
- Hiệp sỹ
-
- 1428 posts
Tiến Sĩ Diễn Đàn Toán
Đánh giá tốt nhất phải là $ \dfrac{6}{5} $
Sử dụng phương pháp xét số chia hết
Sử dụng phương pháp xét số chia hết
Learn from yesterday,live for today,hope for tomorrow
The important thing is to not stop questioning
#3
Khách- thachpbc_*
Posted 10-01-2007 - 18:14
Khách- thachpbc_*
Khách- thachpbc_*
-
- Khách
Biểu diễn $a_i=2^b_ic_i$.
Từ gt suy ra {$c_i|i=1,...,k}$}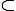
{$1,3,5,...,t$} với $t$ là số lẻ lớn nhất không lớn hơn $n$.
Suy ra $k \leq [ \dfrac{n}{2}] $.
Chú ý có đúng $[ \dfrac{n}{a_i}]$ bội số của $a_i$ mà $<n+1$.
Số các số loại này là phân biệt (vì $[a_i,a_j]>n$).
Từ đó $ \sum\limits_{i=1}^{k}$ $[ \dfrac{n}{a_i}] \leq n.$, nên
$\sum\limits_{i=1}^{k} \dfrac{1}{a_i} \leq \dfrac{k}{n}+1 \leq \dfrac{3}{2}$.
Từ gt suy ra {$c_i|i=1,...,k}$}
{$1,3,5,...,t$} với $t$ là số lẻ lớn nhất không lớn hơn $n$.Suy ra $k \leq [ \dfrac{n}{2}] $.
Chú ý có đúng $[ \dfrac{n}{a_i}]$ bội số của $a_i$ mà $<n+1$.
Số các số loại này là phân biệt (vì $[a_i,a_j]>n$).
Từ đó $ \sum\limits_{i=1}^{k}$ $[ \dfrac{n}{a_i}] \leq n.$, nên
$\sum\limits_{i=1}^{k} \dfrac{1}{a_i} \leq \dfrac{k}{n}+1 \leq \dfrac{3}{2}$.
Edited by thachpbc, 10-01-2007 - 18:17.
#4
Posted 10-01-2007 - 22:29
vnm
-
- Thành viên
-
- 160 posts
Trung sĩ
1 bài gần tương tự
Cho $a_1<a_2...a_n\leq\2n$ Chứng minh rằng
$\min [a_i;a_j]<6(\lfloor\dfrac{n}{2}\rfloor+1)$
Cho $a_1<a_2...a_n\leq\2n$ Chứng minh rằng
$\min [a_i;a_j]<6(\lfloor\dfrac{n}{2}\rfloor+1)$
The day you were born, you cried but the others were smiling; Live your life in a way that one day you die with a smile and all the others cry
#5
Posted 11-01-2007 - 11:20
tanlsth
-
- Hiệp sỹ
-
- 1428 posts
Tiến Sĩ Diễn Đàn Toán
Nếu tồn tại $ 2 $ trong số $ a_i $ có cùng ước số lẻ lớn nhất thì ta có điều phải chứng minh
Nếu các ước số lẻ lớn nhất của các số phân biệt thì nhân thêm $ 2 $ vào các số $ a_i $ ta được các số $ b_i \in [n+1,2n]$
Trong dãy này chứa $ 2([\dfrac{n}{2}]+1) $ và $ 3([\dfrac{n}{2}]+1) $
Suy ra $ [b_i,b_j]= 6[\dfrac{n}{2}]+1) $
Suy ra $ [a_i,a_j] \leq 6[\dfrac{n}{2}]+1) $
Nếu các ước số lẻ lớn nhất của các số phân biệt thì nhân thêm $ 2 $ vào các số $ a_i $ ta được các số $ b_i \in [n+1,2n]$
Trong dãy này chứa $ 2([\dfrac{n}{2}]+1) $ và $ 3([\dfrac{n}{2}]+1) $
Suy ra $ [b_i,b_j]= 6[\dfrac{n}{2}]+1) $
Suy ra $ [a_i,a_j] \leq 6[\dfrac{n}{2}]+1) $
Learn from yesterday,live for today,hope for tomorrow
The important thing is to not stop questioning
1 user(s) are reading this topic
0 members, 1 guests, 0 anonymous users
