Mình có một bài tập nhỏ thế này, các bạn quan tâm và đang học Commutative Algebra thì làm cho vui.
Bài tập:
Cho A là một vành Noetherian (Nơte), I là một ideal thực sự của A và P là một minimal prime ideal (ideal nguyên tố tối tiểu) chứa I. Kí hiệu S = A\P. Hãy chứng minh rằng $ S^{-1}I $ là một $S^{-1}P$ - primary ideal trong $ A_{P} = S^{-1}A $.
Một bài tập về primary ideal (ideal nguyên sơ)
Bắt đầu bởi vinhspiderman, 16-07-2007 - 10:54
#1
Đã gửi 16-07-2007 - 10:54
vinhspiderman
-
- Thành viên
-
- 189 Bài viết
Tồ đại hiệp
Lạy chúa!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
#2
Đã gửi 18-07-2007 - 19:05
nemo
-
- Founder
-
- 416 Bài viết
Hoa Anh Thảo
Mình có một bài tập nhỏ thế này, các bạn quan tâm và đang học Commutative Algebra thì làm cho vui.
Bài tập:
Cho A là một vành Noetherian (Nơte), I là một ideal thực sự của A và P là một minimal prime ideal (ideal nguyên tố tối tiểu) chứa I. Kí hiệu S = A\P. Hãy chứng minh rằng $ S^{-1}I $ là một $S^{-1}P$ - primary ideal trong $ A_{P} = S^{-1}A $.
Tồn tại một tương ứng một-một từ $Spec(A_{P})$ tới tập các ideal nguyên tố của A chứa trong P. Vì vậy $S^{-1}P$ sẽ là ideal nguyên tố tối tiểu của $S^{-1}I$ trong $A_{P}$. Từ $S^{-1}P$ là ideal tối đại duy nhất nên suy ra điều cần chứng minh !
(Hy vọng vẫn còn nhớ đúng một vài điều
)
<span style='color:purple'>Cây nghiêng không sợ chết đứng !</span>
#3
Đã gửi 19-07-2007 - 12:03
vinhspiderman
-
- Thành viên
-
- 189 Bài viết
Tồ đại hiệp
Xin lỗi mọi người và nemo. Mình nghĩ là lời giải của nemo chưa chính xác, không thể không sử dụng giả thiết Noetherian của A được. Về nhà mình ngẫm nghĩ lại mới thấy chỗ chưa chặt chẽ. Hướng giải của nemo gồm 2 ý. Ý đầu tiên thì đúng rồi, $S^{-1}P$ là ideal nguyên tố cực tiểu của $S^{-1}I$. Tuy nhiên ý sau, bạn nói là vì $S^{-1}P$ là ideal cực đại duy nhất nên suy ra ĐPCM (tức là $S^{-1}I$ là một $S^{-1}P$-primary) thì mình thấy chưa rõ ràng. (Chẳng hiểu tại sao hôm ấy mình lại thấy đúng!!)
Bữa giờ bận quá nên nay mới reply được. Dưới đây là lời giải của mình, sử dụng giả thiết Noetherian của A.
Vì A là Noetherian nên I là decomposible, khi đó tập Min(I) gồm hữu hạn ideal là P,P1,...,Pn. Khi đó
$ sqrt{S^{-1}I} = S^{-1} sqrt{I} = S^{-1}( P$
$P1$ ... $Pn = S^{-1}P$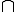 
$S^{-1}P1$ 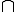... 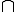$S^{-1}Pn$
Vì $P$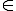
$Min(I)$ nên $Pi$ 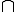$S $ 
do đó $S^{-1}Pi = A_{P} $. Từ đó ta suy ra
$ sqrt{S^{-1}I} = S^{-1}P$, và do đó ta có ĐPCM.
Nếu bạn nào tìm ra lời giải khác hoặc một lời giải mà không cần sử dụng đến tính Noetherian của A thì xin post lên để cùng thảo luận.
Bữa giờ bận quá nên nay mới reply được. Dưới đây là lời giải của mình, sử dụng giả thiết Noetherian của A.
Vì A là Noetherian nên I là decomposible, khi đó tập Min(I) gồm hữu hạn ideal là P,P1,...,Pn. Khi đó
$ sqrt{S^{-1}I} = S^{-1} sqrt{I} = S^{-1}( P$
$P1$ ... $Pn = S^{-1}P$ $S^{-1}P1$ ... $S^{-1}Pn$Vì $P$
$Min(I)$ nên $Pi$ $S $ do đó $S^{-1}Pi = A_{P} $. Từ đó ta suy ra$ sqrt{S^{-1}I} = S^{-1}P$, và do đó ta có ĐPCM.
Nếu bạn nào tìm ra lời giải khác hoặc một lời giải mà không cần sử dụng đến tính Noetherian của A thì xin post lên để cùng thảo luận.
Bài viết đã được chỉnh sửa nội dung bởi vinhspiderman: 26-07-2007 - 17:21
Lạy chúa!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
Con không hề hoài nghi tí nào về sự hiện hữu hoài nghi của người nhưng con hoài nghi rất nhiều về sự minh mẫn và công bình của người!
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh
