lf(x)l

đề KSTN 2001. Help me
#1
 Đã gửi 21-08-2007 - 09:47
Đã gửi 21-08-2007 - 09:47

lf(x)l
#2
 Đã gửi 24-08-2007 - 13:50
Đã gửi 24-08-2007 - 13:50

Mình nghĩ thế này bạn xem có được kô nhaCho $a<b$ và hàm số $f(x)$ có $f'(x)$ liên tục trên$ R$ thỏa mãn $f(a)=f(b)=0$ và $|int\limits_{a}^{b} l f'(x)l dx=m$ .CMR
$lf(x)l \leq \dfrac{m}{2} \forall x \in [a,b]$
Ta chỉ cần chứng minh được rằng :
$ \int\limits_{a}^{b} |f'(x)|dx \geq \int\limits_{a}^{t} |f'(x)|dx+\int\limits_{t}^{b} |f'(x)|dx $ là được
Chứng minh điều này như sau :
Gọi $x_1;x_2;...;x_j \in (a;t)$ là các giá trị sao cho :$f'(x_i)=0$
Ta có : $ \int\limits_{a}^{t}|f'(x)dx =|f(x_i)-f(a)|+... +|f(t)-f(x_{j}| \geq |f(a)-f(t)|=|f(t)| $
Tương tự trên ta có : $ \int\limits_{t}^{b}|f'(x)|dx \geq |f(t)| $
Từ đây suy ra : $ |f(t)| \leq \dfrac{m}{2} \forall t \in (a;b)$
Bài viết đã được chỉnh sửa nội dung bởi DinhCuongTk14: 24-08-2007 - 13:53
#3
 Đã gửi 24-08-2007 - 17:52
Đã gửi 24-08-2007 - 17:52

Liệu chứng mình luôn : Un+1 - Un =
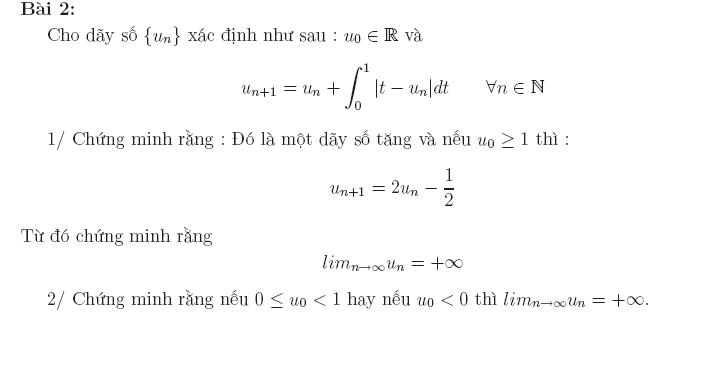
#4
 Đã gửi 24-08-2007 - 18:31
Đã gửi 24-08-2007 - 18:31

Nếu : $ u_1 \geq 1$ thì ta sẽ chứng minh được quy nạp theo $n$ rằng $u_n \geq 1$
Thật vậy $u_n \geq 1 \Rightarrow u_{n+1}=u_n+ \int\limits_{0}^{1}|t-u_n| dt \geq u_n \geq 1 $
Ta đã chứng minh được
Từ đây ta có : $u_{n+1}=u_n + \int\limits_{0}^{1} (u_n-t) dt =2u_n - \dfrac{1}{2} $
Mặt khác : $u_{n+1} - \dfrac{1}{2}=2 .( u_n -\dfrac{1}{2})$
$ \Rightarrow lim_{ n \to +\infty} u_n = + \infty $ .
Bài viết đã được chỉnh sửa nội dung bởi DinhCuongTk14: 24-08-2007 - 18:32
#5
 Đã gửi 24-08-2007 - 18:41
Đã gửi 24-08-2007 - 18:41

+ Với $u_n < 0$ hoặc $u_n >1$ thì ta có :
$u_n+1 \geq u_n + \dfrac{1}{2}$
+ Với $0 \leq u_n \leq 1$ thì :
$ \int\limits_{0}^{1}|t-u_n|dt= \int\limits_{0}^{u_n}(u_n -t ) dt + \int\limits_{u_n}^{1} (t -u_n)dt = \dfrac{1}{2}- (u_n)(1-u_n) \geq \dfrac{1}{4}$
Vậy ta luôn có $u_{n+1} \geq u_n + \dfrac{1}{4}$
Từ đây ta có đpcm
#6
 Đã gửi 26-08-2007 - 20:32
Đã gửi 26-08-2007 - 20:32

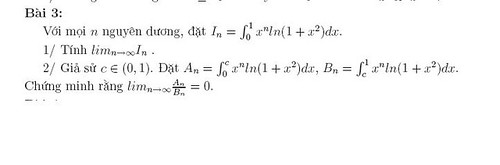
#7
 Đã gửi 26-08-2007 - 22:04
Đã gửi 26-08-2007 - 22:04

Mình làm thử nhaTiếp bài nữa nhé !
Câu 1
Ta có :$ I_n= \int\limits_{0}^{1} x^n ln(1+x^2)dx = \int\limits_{0}^{1} ln(1+x^2)d( \dfrac{x^{n+1}}{n+1})=\dfrac{ln2}{n+1}- \dfrac{2}{n+1}\int\limits_{0}^{1}\dfrac{ x^{n+2}}{x^2 +1}dx$
$I_n = \dfrac{ln2}{n+1}- \dfrac{2}{n+1}U_n$
Với :$ U_n =\int\limits_{0}^{1}\dfrac{ x^{n+2}}{x^2 +1}dx$Đặt $x=tg t$
$U_n= \int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n+2} dt =\int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n}(t^2+1-1) dt= \int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n}d(tgt)-U_{n-2}=\dfrac{1}{n+1}-U_{n-2} $
Từ đây chỉ ra được $lim I_n =0$ .
Không biết có nhầm ở đâu kô nữa
#8
 Đã gửi 31-08-2007 - 22:08
Đã gửi 31-08-2007 - 22:08

Bạn làm phần tính tích phân chậm lại được không ? tắt quá !Câu 1[/color]
Ta có :$ I_n= \int\limits_{0}^{1} x^n ln(1+x^2)dx = \int\limits_{0}^{1} ln(1+x^2)d( \dfrac{x^{n+1}}{n+1})=\dfrac{ln2}{n+1}- \dfrac{2}{n+1}\int\limits_{0}^{1}\dfrac{ x^{n+2}}{x^2 +1}dx$
$I_n = \dfrac{ln2}{n+1}- \dfrac{2}{n+1}U_n$
Với :$ U_n =\int\limits_{0}^{1}\dfrac{ x^{n+2}}{x^2 +1}dx$Đặt $x=tg t$
$U_n= \int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n+2} dt =\int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n}(t^2+1-1) dt= \int\limits_{0}^{\dfrac{\pi}{4}}(tgt)^{n}d(tgt)-U_{n-2}=\dfrac{1}{n+1}-U_{n-2} $
Từ đây chỉ ra được $lim I_n =0$ .
Không biết có nhầm ở đâu kô nữa. Các bạn giúp mình kiểm tra lời giải nhé
#9
 Đã gửi 03-09-2007 - 15:33
Đã gửi 03-09-2007 - 15:33

1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh



