1)Tìm $x,y\epsilon N$ sao cho $2^x+5^y $là số chính phương.
2)CMR: Nếu các số nguyên a,b,c thỏa mãn: $b^2-4ac$ và $b^2+4ac$ đồng thời là các số chính phương thì $a.b.c\vdots 30$

Vài bài khó!
Bắt đầu bởi nathien095, 02-12-2009 - 15:37
#1
 Đã gửi 02-12-2009 - 15:37
Đã gửi 02-12-2009 - 15:37

#2
 Đã gửi 03-12-2009 - 11:24
Đã gửi 03-12-2009 - 11:24

2/
*Chú ỷ rằng một số chính phương chia 8 dư 0;1 hoặc 4.
a. $ b^2 \equiv 0;4 (mod 8) <=> b \vdots 2 <=> abc \vdots 2 $
b. $ b^2 \equiv 1 (mod 8) & b^2-4ac \equiv 0;1;4 (mod 8) <=> 4ac \vdots 8 <=> ac \vdots 2 <=> abc \vdots 2$
*Một số chính phương chia 3 dư 0 hoặc 1.
a. $ b^2 \equiv 0 (mod 3) <=> b \vdots 3 <=> abc \vdots 3 $
b. $ b^2 \equiv 1 (mod 3) & b^2-4ac \equiv 0;1 (mod 3) <=> 4ac \equiv 0;1 (mod 3)$
$ b^2 \equiv 1 (mod 3) & b^2+4ac \equiv 0;1 (mod 3) <=> 4ac \equiv 0;2 (mod 3)$
$\rightarrow 4ac \equiv 0 (mod 3) <=> ac \equiv 0 (mod 3) (do (3,4)=1) <=> abc\vdots 3$
*Một số chính phương chia 5 dư o;1 hoặc 4.
a.$b^2 \vdots 5 <=> abc \vdots 3$
b. $b^2 \equiv 1 (mod 5); b^2-4ac \equiv 0;1;4 (mod 5) <=> 4ac \equiv 1;0;2 (mod 5)$
$b^2+4ac \equiv 0;1;4 (mod 5) <=> 4ac \equiv 4;0;3$
Vậy $4ac \equiv 0 (mod 5) <=> abc \vdots 5$
* Do (2,3,5)=1 $=>abc \vdots (2.3.5=30)$
*Chú ỷ rằng một số chính phương chia 8 dư 0;1 hoặc 4.
a. $ b^2 \equiv 0;4 (mod 8) <=> b \vdots 2 <=> abc \vdots 2 $
b. $ b^2 \equiv 1 (mod 8) & b^2-4ac \equiv 0;1;4 (mod 8) <=> 4ac \vdots 8 <=> ac \vdots 2 <=> abc \vdots 2$
*Một số chính phương chia 3 dư 0 hoặc 1.
a. $ b^2 \equiv 0 (mod 3) <=> b \vdots 3 <=> abc \vdots 3 $
b. $ b^2 \equiv 1 (mod 3) & b^2-4ac \equiv 0;1 (mod 3) <=> 4ac \equiv 0;1 (mod 3)$
$ b^2 \equiv 1 (mod 3) & b^2+4ac \equiv 0;1 (mod 3) <=> 4ac \equiv 0;2 (mod 3)$
$\rightarrow 4ac \equiv 0 (mod 3) <=> ac \equiv 0 (mod 3) (do (3,4)=1) <=> abc\vdots 3$
*Một số chính phương chia 5 dư o;1 hoặc 4.
a.$b^2 \vdots 5 <=> abc \vdots 3$
b. $b^2 \equiv 1 (mod 5); b^2-4ac \equiv 0;1;4 (mod 5) <=> 4ac \equiv 1;0;2 (mod 5)$
$b^2+4ac \equiv 0;1;4 (mod 5) <=> 4ac \equiv 4;0;3$
Vậy $4ac \equiv 0 (mod 5) <=> abc \vdots 5$
* Do (2,3,5)=1 $=>abc \vdots (2.3.5=30)$
#3
 Đã gửi 03-12-2009 - 12:52
Đã gửi 03-12-2009 - 12:52

1,xet x=0;1;2 va x 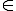 3
3
Bài viết đã được chỉnh sửa nội dung bởi phuc_007: 03-12-2009 - 12:53
không có gì là không thể nhưng điều này không có nghĩa là điều gì cũng có thể
#4
 Đã gửi 03-12-2009 - 21:22
Đã gửi 03-12-2009 - 21:22

bạn phuc 007 ơi giải thích kĩ hơn bài 1 đi mình không hiểu cho lắm
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh




