

Laurent Lafforgue vừa dọn tới phòng làm việc mới. Ông mới được bổ nhiệm giữ chức phụ trách bộ môn hình học đại số của Viện nghiên cức khoa học cao cấp (IHES) – một viện nghiên cứu toán học và vật lý toán nổi tiếng thế giới, đặt tại Bures-sur-Yvette, gần Paris. Đây cũng là một trong những cương vị có uy tín nhất trong thế giới toán học.
Nhà toán học trẻ người Pháp 33 tuổi này đã làm nên công trạng gì mà lại được hưởng một vinh dự cao quý như vậy? Theo lời ông Jean-Pierre Bourguignon, giám đốc Viện này và là người ký quyết định bổ nhiệm Lafforgue thì Laurent Lafforgue vừa mới chứng minh được trọn vẹn một phần trong chương trình của Langlands. Đây là một công trình tuyệt vời. Rất nhiều nhà toán học đã cho rằng công việc này phải mất mấy chục năm nữa mới có thể hoàn thành.
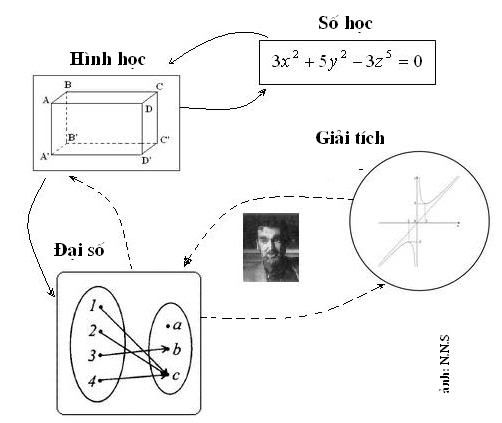
Vậy chương trình Langlands là gì? Ngoài một số hạn chế các nhà toán học ra, ít người được nghe nói về nó. Dự án bí ẩn này thực ra là nhằm đặt mối quan hệ giữa các đối tượng toán học phức tạp và trừu tượng nhất đã từng được tạo ra và những phương tiện cần thiết để chứng minh được điều đó cũng phức tạp không kém... Tuy nhiên, chương trình Langlands có một mục đích được phát biểu một cách đơn giản như sau: tạo ra những nhịp cầu nối giữa số học, hình học, đại số và giải tích, lập một cuốn ìtừ điển” giữa các ngôn ngữ toán học khác nhau.
Thực tế các nhà toán học không xem xét các sự vật theo cùng một cách và do vậy họ không nói cùng một ngôn ngữ. Nhà số học xét các con số, nhà hình học xét các hình dạng, nhà đại số xét các quan hệ còn nhà giải tích xét các biến thiên. Chương trinh Langlands hứa hẹn với họ rằng, cuối cùng, họ sẽ có thể giao lưu được với nhau. Nói một cách văn hoa thì cuối cùng trong tháp Babel toán học người ta rồi sẽ nói chỉ một ngôn ngữ - ngôn ngữ phổ quát, ngôn ngữ cho thấy bản chất sâu xa của các sự vật.
Đối tượng ban đầu của toán học là số nguyên 1, 2, 3… và số học, tức sự nghiên cứu những quan hệ giữa các số nguyên ấy, chính là ngôn ngữ nguyên thủy của chúng. “Chúa đã tạo ra các số nguyên và con người sáng chế ra những thứ còn lại” – đó là lời tổng kết ở thế kỷ trước của nhà toán học Đức Leopold Kronecker. Các phép tính được phép đối với các số nguyên chỉ là phép cộng, trừ, nhân và chia. Vốn từ vựng của số học cũng rất hạn chế, nhưng chúng cũng đủ để đặt ra những bài toán mà tới tận hôm nay cũng chưa ai giải được.
Một ví dụ về bài toán học số học kinh điển là nghiên cứu phương trình $x^2 + y^2 = z^2$. Liệu có tồn tại những số nguyê hay phân số thỏa mãn phương trình đó hay không? Nếu có, thì có bao nhiêu nghiệm? nhờ ít phép tính đơn giản, các nhà toán học cổ Hy Lạp đã tìm ra lời giải đúng: phương trình trên có nghiệm (ví dụ: $4^2 + 3^2 = 5^2$) và thậm chí còn có vô số nghiệm.

“Chúa đã tạo ra các số nguyên và con người sáng chế ra những thứ còn lại”
Leopold Kronecker (1823-1891) nhà toán học Đức
CÁC PHƯƠNG TRÌNH DIOPHANTE
Từ Diophante ở thế kỷ IV tới Pierre Fermat ở thế kỷ XVII, những người say mê số học đã mở rộng dần câu hỏi trên cho tất cả các phương trình cùng loại (được gọi là các phương trình Diophante) bất kể bậc, số ẩn và các hệ số của chúng. Chẳng hạn, liệu người ta có tính được nghiệm của phương trình $3x^3 – 7x^2 + 23y^2 – 4z = w^2$ không? Thật không may, những phép tính số học ở đây trở nên rất phức tạp. Cả Diophante lẫn Fermat đều không có các phương tiện để tìm được câu trả lời tổng quát. Do vậy các phương trình Diophante – đối tượng cơ bản của số học – vẫn giữ kín những bí mật của chúng…
Tuy nhiên các nhà toán học vốn là những người ương bướng. Do ngôn ngữ số học không thể giải được bài toán này, họ bèn thử ìphiên dịch” nó sang một ngôn ngữ khác, ngôn ngữ hình học. Sự nghiên cứu các hình không gian chỉ thực sự tấn công các bài toán số học bắt đầu từ năm 1637, khi nhà toán học Pháp René Descartes đưa ra khái niệm hệ tọa độ không gian. Descartes muốn quy mọi bài toán về hình học. Ông biêu diễn các điểm trong một mặt phẳng bằng cặp hoành độ và tung độ $(x,y)$ của chúng. Như vậy, tập hợp nghiệm của một phương trình Diophante hai ẩn sẽ được biểu diễn bằng hình học bởi một đường cong. Ví dụ, phương trình $y = 2x + 1$ bây giờ trở thành một đường thẳng. Khi có ba ẩn số, đường cong sẽ trở thành một mặt. Và, nếu có bốn ẩn số hoặc nhiều hơn thì ta sẽ khó hình dung được tập hợp nghiệm, nhưng ngôn ngữ hình học vẫn còn giữ nguyên giá trị. Nhờ các tọa độ Descartes này mà bài toán số học bây giờ có thể được dịch thành bài toán hình học (và ngược lại). Và sự nghiên cứu các phương trình Diophante đã có những tiến bộ nhất định trong sự phiên dịch này: nếu số học là ngôn ngữ nguyên thủy của toán học thì hình học là ngôn ngữ tự nhiên nhất và trực giác nhất của nó.
Dẫu sao, sự ghép đôi giữa số học và hình học còn xa mới đạt tới mức hoàn hảo: ngôn ngữ hình học không cho phép phân biệt được những điểm có tọa độ nguyên và các điểm có tọa độ bất kỳ, vì vậy không cho phép mô tả một cách thuận lợi các phương trình Diophante.
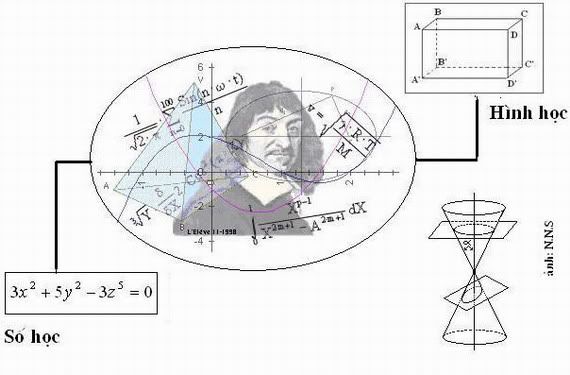
Chính khi này các nhà vật lý đã vào cuộc. Trong suốt cuối thế kỷ XVII, nhà bác học Isaac Newton có một bài toán: đó là tìm cách hình thức hóa sự tiến triển của các hiện tượng vật lý, như quỹ đạo của một viên đạn hay sự rơi của một quả táo. Mục đích ở đây không phải là nghiên cứu các hình dạng mà là sự biến thiên. Tuy nhiên, các công cụ của hình học, là thước và compa, không thích hợp đối với vấn đề này.
Cùng với nhà toán học người Đức Wilhelm Leibniz, Newtonđã sử dụng các tọa độ Descartes để tạo ra một ngôn ngữ toán học mới: đó là giải tích. Bây giờ người ta không nói về các ẩn, các phương trình, các tọa độ và các đường cong nữa mà là nói về các biến và các hàm. Đạo hàm, tích phân, các phép tính giới hạn và nghiên cứu về tính liên tục, tức toàn bộ kho công cụ của giải tích đã được xây dựng. Tuy nhiên, nếu giải tích đã trở thành một trong số những ngôn ngữ mạnh nhất của toán học thì vốn từ vựng của nó cũng vẫn chưa cho phép diễn đạt một cách thuận tiện các tính chất của phương trình Diophante.
MỘT LÝ THUYẾT CÓ TÍNH CÁCH MẠNG
Phải đợi tới ngày 30 tháng 5 năm 1832, bài toán cổ nói trên mới có bước tiến đáng kể. Trước hôm đấu súng, biết chắc mình sẽ chết, trong bức thư tuyệt mệnh của mình, Evarist Galois, lúc đó mới 20 tuổi, đã vội vã ghi lại một lý thuyết có tính chất cách mạng về các phương trình Diophante.
Galois cho rằng không nên phí thời gian đi tính nghiệm của các phương trình đó, mà hay hơn là nên tập trung nghiên cứu các quan hệ tồn tại giữa các nghiệm khác nhau của chúng. Những nghiệm này (sẽ trở nên vô ích để tìm kiếm) tạo thành một tập hợp có tên là ìbiểu diễn Galois” của phương trình. Nhà toán học trẻ đã chứng minh được rằng chỉ cần biết cấu trúc của tập hợp đó là ta biết được các tính chất của phương trình xuất phát. Galois cũng là người đã phát minh ra phương pháp dịch hai ngôn ngữ cũ là số học và hình học sang ngôn ngữ đại số - ngôn ngữ nghiên cứu những quan hệ giữa các phần tử khác nhau cùng cùng một tập hợp. Phải sau khi ông mất nhiều thập niên người ta mới bắt đầu hiểu được tầm quan trọng công trình của ông, nhưng theo Laurent Lafforgue thì “phát minh của Galois, có lẽ, là phát minh thiên tài nhất của mọi thời đại… ngày hôm nay nó vẫn còn là trung tâm của số học và toàn bộ toán học nói chung”.
Galois mới chỉ áp dụng phương pháp dịch có tính cách mạng của mình cho một trường hợp tương đối đơn giản, đó là phương trình Diophante một ẩn (có dạng $a_nx^n + a_{n-1}x^(n-1) + … + a_1x + a_0 = 0$, với $a_n … a_0$ là các số nguyên); phương trình loại này chỉ có hữu hạn nghiệm và biểu diễn Galois của nó là một tập hợ có hữu hạn phần tử. Người ta có thể biết được cấu trúc của tập hợp hữu hạn này không mấy khó khăn. Lý thuyết Galois cũng cho phép chứng minh một cách rất đơn giản rằng các phương trình nói trên có bậc lớn hơn 4 nói chung không thể biểu diễn qua các số nguyên, phân số và căn thức.
Thật tiếc là phương pháp dịch có hiệu quả này lại không thể dùng được cho các phương trình có nhiều ẩn số. Lúc này tập hợp nghiệm không còn là tập hợp rời rạc của những con số đơn độc nữa mà là một tập hợp liên tục như một đường cong hoặc một mặt. Các nhà toán học đã phải mất một thời gian rất lâu để tìm cách định nghĩa biểu diễn Galois gắn liền với các đối tượng số học và hình học đó. Trong hơn một thể kỷ chưa có ai định nghĩa được đúng biểu diễn này, đây là các đối tượng đại số tinh tế ẩn chứa những tính chất số học của các phương trình Diophante.
MỘT CUỐN TỪ ĐIỀN HOÀN CHỈNH
Người Pháp ở thế kỷ XX đã đương đầu với công việc này. André Weil đã chỉ ra các phương hướng nghiên cứu lớn, Jean-Pierre Serre đã nhận được một số kết quả, nhưng Alexandre Grothendieck mới là người làm phần lớn công việc. Trong một công trình vĩ đại được thực hiện trong thời gian từ 1958 đên 1970, nhà toán học người Pháp gốc Đức này (cũng làm việc ở IHES) chỉ một mình đã tổng quát hóa thành công lý thuyết của Galois. Ông đã định nghĩa đúng biểu diễn Galois gắn liền với bất cứ một phương trình (hay hệ phương trình) Diophante nào và do đó đã lập được một cuốn từ điển hoàn chỉnh cho phép dịch một bài toán số - hình học thành một bài toán thuần túy đại số. ìVào thời đó, phòng làm việc của Grothendieck là trung tâm của thế giới toán học” – Laurent Lafforgue kể lại một cách thán phục.
Tuy vậy, cuốn từ điển này chỉ tra được một chiều, từ ngôn ngữ hình học sang ngôn ngữ đại số. Nó cho phép thay việc nghiên cứu một phương trình Diophante bằng nghiên cứu biểu diễn Galois của nó. Nhưng điều này tiến bộ hơn ở chỗ nào? Biết đâu sự dịch này chẳng qua chỉ làm chuyển đổi bài toán mà thôi. Hơn nữa, làm thế nào nghiên cứu được cấu trúc của tập hợp đại số mới này, nơi che giấu những bí mật của phương trình?
Từ khi ra đời công trình nền tảng của Galois, câu hỏi này luôn luôn dày vò đầu óc tất cả các nhà toán học trên thế giới. Phải cần cả trăm năm để cho một lời giải táo bạo, lạ lùng và mẫu mực xuất hiện: để biết cấu trúc của một đối tượng đại số cần phải dịch nó thành đối tượng giải tích. Sau khi đã chuyển đổi một bài toán số học thành đại số và bây giờ lại cần chuyển đổi từ đại số sang ngôn ngữ lớn cuối cùng của toán học vẫn còn đứng riêng rẽ, đó là giải tích. Khi đó các công cụ của giải tích sẽ cho phép ta biết một cách hoàn hảo cấu trúc của đối tượng đại số đó.
Sau một trăm năm lỗ lực, cuối cùng vào năm 1930, nhà số học người Áo Emil Artin đã thực hiện được một phần của sự phiên dịch đó. Ông đã thành công lập được sự tương ứng giữa một số biểu diễn Galois (gọi là “giao hoán”) với các hàm tuần hoàn đặc biệt và như vậy đã lập được cầu nối giữa đại số và giải tích điều hòa – một lĩnh vực toán học được phát minh bởi nhà toán học Pháp Joseph Fouier (1768-1830) để phân tích các sóng. Vấn đề khó nhất vẫn cần phải làm, đó là tìm một công thức chung để lập sự tương ứng giữa một hàm giải tích với tất cả các biểu diễn Galois khác (tức là các biểu diễn “không giao hoán”, chúng nhiều hơn về số lượng và giàu thông tin hơn).

Robert Langlands (1930- ), nhà toán học lớn người Canada, một trong những nhà toán học lớn nhất thế kỷ trước với những đóng góp quan trọng về lý thuyết số và lý thuyết biểu diễn. Giải thưởng Wolf năm 1996 cho chương trình Langlands
Emil đã tốn hơn 30 năm để tìm kiếm công thức này nhưng đã không tìm ra. Năm 1955, một nhà toán học Nhật Bản tên là Yukata Taniyama đã đề xuất, nhưng không chứng minh, một công thức áp dụng cho các biểu diễn Galois liên quan với các phương trình eliptic. Nhưng cuối cùng, trong một bức thư gửi cho André Weil vào tháng 1 năm 1967, nhà toán học Canada Robert Langlands đã phát biểu một phương pháp chung xác lập sự tương ứng đó. Ông đã nêu ra một tập hợp các hàm điều hòa đặc biệt có tương ứng 1-1 với các biểu diễn Galois còn lại. Vậy là toàn bộ các đối tượng đại số đã có tương đương giải tích của chúng. Robert Langlands chưa chứng minh được sự tương ứng sâu sắc này, nhưng ông đã tìm được nhiều kết quả và luận chứng có sức thuyết phục để làm cơ sở cho trực giác của mình. Việc chứng minh sự tương ứng này quan trọng đối với sự nghiên cứu các con số tới mức nó trở thành cả một chương trình – chương trình Langlands.
Tuy nhiên, chương trình Langlands – cầu nối các lý thuyết toán học phức tạp nhất – rất không may lại khó chưa từng thấy. Chính vì vậy mà năm ngoái (tức năm 2000 – ngocson52) cả cộng đồng toán học phải sững sờ khi một nhà toán học trẻ người Pháp tuyên bố đã một mình hoàn thành toàn bộ một phần của chương trình đó!
MỘT SỰ ĐỐI XỨNG TUYỆT ĐỐI
Thực tế, chứng minh của Laurent Lafforgue không liên quan tới tập hợp các số nguyên. Nó được hạn chế trong một tập hợp trừu tượng hơn rất nhiều, nhưng dễ nghiên cứu hơn: đó là tập hợp các hàm gắn một giá trị với mỗi điểm thuộc một đường cong. “Trong suốt nửa đầu thế kỷ XX, các nhà toán học đã nhận thấy rằng ứng với mỗi một luật đúng đối với các con số sẽ có một luật tương tự đúng với các hàm” – Laurent Lafforgue giải thích. Trong thế giới các con số, Langlands đã bắc một nhịp cầu giữa đại số và giải tích. Nhưng vì có một sự đối xứng tuyệt đối giữa thế giới các con số nên cũng sẽ có một chương trình Langlands đúng cho thế giới các hàm.
Trong những năm 1970, nhà toán học Ucraina Vladimir Drinfeld đã phác thảo một chứng minh cho chương trình này và đã xét một trường hợp đặc biệt có tính chất quyết định. Ba mươi năm sau, sau bảy năm rưỡi đơn thương độc mã nghiên cứu hơn 600 trang trình bày, Laurent Lafforgue đã hoàn tất chương trình của Drinfeld . “Tôi sẽ không đạt được gì nếu không có công trình của Drinfeld” – Laurent nhấn mạnh. “Tôi chỉ nghiên cứu các đối tượng do ông phát minh ra và tổng quát hóa những chứng minh của ông ấy”. Sau khi đã bị thất bại trong lần chứng minh đầu tiên của mình vào năm 1999, nhà toán học trẻ người Pháp cuối cùng đã thống nhất được các ngôn ngữ đại số và giải tích vào mùa hè năm 2000.
Nhưng thế thì sao? Nếu chương trình đã được chứng minh với các hàm thì cũng tức là nó cũng sẽ đúng đối với các số vì hai thế giới này là hoàn toàn đối xứng với nhau! Điều này quá là đẹp. Nhưng sự tương tự không thể dùng để làm chứng minh. Vì vậy tất cả vẫn còn phải làm với các con số. Và trong lĩnh vực này sự tiến bộ rất là chậm chạp.
Tuy nhiên, gần đây đã có những tiến bộ đáng kể. Năm 1994, khi chứng minh một định lý nổi tiếng của số học có tên là “định lý cuối cùng của Fermat”, nhà toán học người Anh Andrew Wiles đã chứng minh được công thức của Taniyama, công thức dịch các phương trình eliptic thành các đối tượng giải tích. Nhưng hiện chưa ai biết tới thế kỷ nào chương trình Langlands mới được hoàn tất…
Dù sao, sự hoàn tất chương trình đó cũng sẽ không giải quyết được dứt điểm bài toán cổ xưa về các phương trình Diophante. Cái cầu giữa hình học và đại số thực tế vẫn là chiếc cầu một chiều. Người ta biết cách dịch các phương trình thành những biểu diễn Galois, nhưng làm thế nào dịch các biểu diễn này thành các phương trình? Để cho các nhà toán học về các phương trình Diophante nói cùng một ngôn ngữ phổ quát cần phải cho phép chiếc cầu nối này có chiều ngược lại, tức là từ đại số đến hình học.
Alexander Grothendieck đã một mình chìm đắm trong nghiên cứu về sự dịch tối hậu đó. Ông đã vẽ ra một phác thảo về nó – “lý thuyết về các motif” – nhưng chưa thiết lập được một cách chặt chẽ cơ sở của nó. “Đây là lần đầu tiên trong cuộc đời mình Grothedieck đã phải đương đầu với một bài toán mà ông không giải được” – Laurent kể. Giống như chàng Icar tiến quá gần tới Mặt Trời, Grothedieck,người được xem là một trong số các nhà toán học vĩ đại nhất của mọi thời đại, đã đột ngột dừng nghiên cứu toán học vào năm 1970 và rời IHES. Một vài năm sau, ông đã giã từ thế giới văn minh và lui về sống cuộc đời của một tu sĩ.

Laurent Lafforgue (1966 - ), nhà toán học Pháp, giải thưởng Fields năm 2002
Bỏ lại sau lý thuyết các motif cò dang dở, Alexander Grothedieck đã trao lại cho các nhà toán học những từ bập bẹ đầu tiên của một ngôn ngữ phổ quát mà chưa ai biết nói. Giờ đây Laurent Lafforgue đã rời Đại học Orsay để kế vị ông ở IHES. Trên bàn làm việc mới của Lafforgue, bên cạnh bức ảnh của Grothedieck là một tờ giấy trắng và một chiếc bút chì…
PHẠM VĂN THIỀUdịch từ tạp chí Science et Vie (Theo tạp chí Tia Sáng, tháng 5.2001)
Minh họa hình ảnh và chú thích: ngocson52
BBT: Bài viết được viết từ 2001 nên chưa có sự kiện GS Ngô Bảo Châu chứng minh thành công Bổ đề cơ bản. BBT xin mời các bạn cùng thảo luận tại: http://diendantoanho...p?showtopic=521
Bài viết đã được chỉnh sửa nội dung bởi Ban Biên Tập: 09-05-2012 - 21:47








