Chủ đề này có 3 trả lời

[soclocchocnhuconcoc]

Cho dãy số thực ()
$ \left\{ \begin{array}{l} a_1 = 1 \\ a_{n + 1} = a_n + \dfrac{1}{{a_n }}(n \ge 1) \\ \end{array} \right. $
Chứng minh:
$\lim \dfrac{{a_n }}{{\sqrt n }} = \sqrt 2 $

Bài viết đã được chỉnh sửa nội dung bởi dark templar: 09-05-2011 - 13:35
Latex+Cảnh cáo về Tiêu đề

[alex_hoang]

Cho dãy số thực ()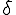
$ \left\{ \begin{array}{l} a_1 = 1 \\ a_{n + 1} = a_n + \dfrac{1}{{a_n }}(n \ge 1) \\ \end{array} \right. $
Chứng minh:
$\lim \dfrac{{a_n }}{{\sqrt n }} = \sqrt 2 $

mình chém luôn nha
Ta có
$a_{k + 1}^2 = a_k^2 + \dfrac{1}{{a_k^2}} + 2 \Rightarrow \sum\limits_{1 = 1}^n {a_i^2} = \sum\limits_{j = 1}^{n - 1} {a_j^2} + \sum\limits_{j = 1}^{n - 1} {\dfrac{1}{{a_j^2}}} + 2(n - 1) \to a_n^2 = 2n - 1 + \sum\limits_{j = 1}^{n - 1} {\dfrac{1}{{a_j^2}}} \to {a_n} > \sqrt {2n - 1} \forall n \ge 2 \to a_k^2 > 2k - 1,\forall k \ge 2 \Rightarrow \dfrac{1}{{a_k^4}} < \dfrac{1}{{{{(2k - 1)}^2}}} < \dfrac{1}{{4k(k - 1)}} = \dfrac{1}{4}(\dfrac{1}{{k - 1}} - \dfrac{1}{k}) \to \sum\limits_{k = 2}^{n - 1} {\dfrac{1}{{a_k^4}}} < \dfrac{1}{4}(1 - \dfrac{1}{{n - 1}}) < \dfrac{1}{4} \to \sum\limits_{k = 1}^{n - 1} {\dfrac{1}{{a_k^4}}} < \dfrac{5}{4} \to \sum\limits_{j = 1}^{n - 1} {\dfrac{1}{{a_j^2}}} \le \sqrt {(n - 1)\sum\limits_{k = 2}^{n - 1} {\dfrac{1}{{a_k^4}}} } < \sqrt {(n - 1)\dfrac{5}{4}} \to a_n^2 < 2n - 1 + \sqrt {(n - 1)\dfrac{5}{4}} $
$\forall n \ge 2,\sqrt {2n - 1} < {a_n} < \sqrt {2n - 1 + \sqrt {(n - 1)\dfrac{5}{4}} } \to \sqrt {2 - \dfrac{1}{n}} < \dfrac{{{a_n}}}{{\sqrt n }} < \sqrt {2 - \dfrac{1}{n} + \sqrt {(\dfrac{1}{n} - \dfrac{1}{{{n^2}}})\dfrac{5}{4}} } \to \mathop {\lim }\limits_{n \to + \infty } \dfrac{{{a_n}}}{{\sqrt n }} = \sqrt 2 $

[Messi_ndt]

Cho dãy số thực ()
$ \left\{ \begin{array}{l} a_1 = 1 \\ a_{n + 1} = a_n + \dfrac{1}{{a_n }}(n \ge 1) \\ \end{array} \right. $
Chứng minh:
$\lim \dfrac{{a_n }}{{\sqrt n }} = \sqrt 2 $

Ta có $x_{n+1}=x_n+\dfrac{1}{x_n}\Rightarrow x_{n+1}^2=x_n^2+\dfrac{1}{x_n^2}+2\Rightarrow x_{n+1}^2-x_n^2=2+\dfrac{1}{x_n^2}$
mà ta đã CM được $\lim x_n=+\infty$, do đó $\lim \left ( x_{n+1}^2-x_n^2 \right )=2$
áp dụng định lý Stolz, ta suy ra $\lim \dfrac{x_n^2}{n}=2\Rightarrow \lim \dfrac{x_n}{\sqrt n}=\sqrt2$

[alex_hoang]

Ta có $x_{n+1}=x_n+\dfrac{1}{x_n}\Rightarrow x_{n+1}^2=x_n^2+\dfrac{1}{x_n^2}+2\Rightarrow x_{n+1}^2-x_n^2=2+\dfrac{1}{x_n^2}$
mà ta đã CM được $\lim x_n=+\infty$, do đó $\lim \left ( x_{n+1}^2-x_n^2 \right )=2$
áp dụng định lý Stolz, ta suy ra $\lim \dfrac{x_n^2}{n}=2\Rightarrow \lim \dfrac{x_n}{\sqrt n}=\sqrt2$

Cách của bạn ngắn thật đấy nhưng phải sử dụng định lí Stolz của chương trình đại học cách của mình tuy dài hơn nhưng chỉ sử dung kiến thức cấp 3