Chủ đề này có 24 trả lời

[caubeyeutoan2302]

Bài 1: Giải phương trình:
$(2cos\dfrac{\pi}{7}-\dfrac{1}{2cos\dfrac{\pi}{7}})^{x}=1+(4cos^2\dfrac{\pi}{7}-3)^{x}$
Bài 2: Chứng minh rằng trong tam giác nhọn ABC, ta luôn có:
$ (tanA)^{tanA}.(tanB)^{tanB}.(tanC)^{tanC} \ge (\sqrt{3})^{3\sqrt{3}}$
Bài 3:
Cho tam giác ABC là tam giác nhọn , hãy xác định dạng của tam giác biết rằng:
$tan^6\dfrac{A}{2}+tan^6\dfrac{B}{2}+tan^6\dfrac{C}{2}=\dfrac{1}{9}$

[vietfrog]

Chủ nhân bài viết thực sự thấy xấu hổ vì cách làm và trình bày của mình nên muôn sửa lại cách trình bày. (
Ta có:
Theo BDT AM-GM:
$\sum {{{\tan }^6}\dfrac{A}{2}} \ge \sum {{{\tan }^2}\dfrac{A}{2}} $
Mặt khác:
Theo BDT Cauchy-Shwarz:
$1 \le 3\sum {{{\tan }^2}\dfrac{A}{2}} .{\tan ^2}\dfrac{B}{2} \Leftrightarrow \dfrac{1}{9} \le {(\sum {{{\tan }^2}\dfrac{A}{2}} )^2}$

$ \Rightarrow \sum {{{\tan }^2}\dfrac{A}{2}} \ge \dfrac{1}{9}$

$ \Rightarrow \sum {{{\tan }^6}\dfrac{A}{2}} \ge \dfrac{1}{9}\$

Dấu = khi $A = B = C$

Bài viết đã được chỉnh sửa nội dung bởi vietfrog: 18-07-2011 - 07:31

[caubeyeutoan2302]

Mệt quá. Mãi mới được một bài.
Trong bài sẽ sử dụng một số Bất đẳng thức, Hằng đẳng thức quen thuộc :
BĐT Cauchy-Shwarz , hệ thức $\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{C}{2}.\tan \dfrac{A}{2} = 1$
Bài làm
Áp dụng BĐT Cauchy-Shwarz ta được :

${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{B}{2}.\tan \dfrac{C}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3}$(1)
Ta lại có:
$1 = {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{A}{2}.\tan \dfrac{C}{2})^2} \le 3({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})$

$->\dfrac{1}{3} \le ({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})$
Bình phương hai vế:
$->\dfrac{1}{9} \le {({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})^2}$

$->\dfrac{1}{9} \le {\left[ {\sqrt {\tan \dfrac{A}{2}.\tan \dfrac{B}{2}} .\sqrt {{{(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})}^3}} + \sqrt {\tan \dfrac{B}{2}.\tan \dfrac{C}{2}} .\sqrt {{{(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})}^3}} + \sqrt {\tan \dfrac{C}{2}.\tan \dfrac{A}{2}} .\sqrt {{{(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})}^3}} } \right]^2}$
Áp dụng BĐT Cauchy-Shwarz lần nữa ta được:
$\dfrac{1}{9} \le ((\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{C}{2}.\tan \dfrac{A}{2})({(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3})$
Sử dụng hệ thức ta có:
$->\dfrac{1}{9} \le {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3}$(2)
Từ (1),(2)
${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge \dfrac{1}{9}$

Dấu = khi $A = B = C$
Vậy tam giác ABC đều!
P/s: Kí hiệu Xích ma và suy ra bị hỏng, gõ mệt quá. Hơi rối mắt, sorry mọi người ...)

Cách giải của anh làm em rất ấn tượng ạ, thanks anh:
Bài toán tổng quát:Cho tam giác ABC. Chứng minh với n là số nguyên dương ta có:
$tg^{2n}\dfrac{A}{2}+tg^{2n}\dfrac{B}{2}+tg^{2n}\dfrac{C}{2} \ge \dfrac{1}{3^{n-1}}$

Bài viết đã được chỉnh sửa nội dung bởi caubeyeutoan2302: 17-07-2011 - 21:56

[Nguyễn Hoàng Lâm]

Mệt quá. Mãi mới được một bài.
Trong bài sẽ sử dụng một số Bất đẳng thức, Hằng đẳng thức quen thuộc :
BĐT Cauchy-Shwarz , hệ thức $\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{C}{2}.\tan \dfrac{A}{2} = 1$
Bài làm
Áp dụng BĐT Cauchy-Shwarz ta được :

${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{B}{2}.\tan \dfrac{C}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3}$(1)
Ta lại có:
$1 = {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{A}{2}.\tan \dfrac{C}{2})^2} \le 3({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})$

$->\dfrac{1}{3} \le ({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})$
Bình phương hai vế:
$->\dfrac{1}{9} \le {({\tan ^2}\dfrac{A}{2}.{\tan ^2}\dfrac{B}{2} + {\tan ^2}\dfrac{B}{2}.{\tan ^2}\dfrac{C}{2} + {\tan ^2}\dfrac{C}{2}.{\tan ^2}\dfrac{A}{2})^2}$

$->\dfrac{1}{9} \le {\left[ {\sqrt {\tan \dfrac{A}{2}.\tan \dfrac{B}{2}} .\sqrt {{{(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})}^3}} + \sqrt {\tan \dfrac{B}{2}.\tan \dfrac{C}{2}} .\sqrt {{{(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})}^3}} + \sqrt {\tan \dfrac{C}{2}.\tan \dfrac{A}{2}} .\sqrt {{{(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})}^3}} } \right]^2}$
Áp dụng BĐT Cauchy-Shwarz lần nữa ta được:
$\dfrac{1}{9} \le ((\tan \dfrac{A}{2}.\tan \dfrac{B}{2} + \tan \dfrac{B}{2}.\tan \dfrac{C}{2} + \tan \dfrac{C}{2}.\tan \dfrac{A}{2})({(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3})$
Sử dụng hệ thức ta có:
$->\dfrac{1}{9} \le {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{A}{2}.\tan \dfrac{B}{2})^3} + {(\tan \dfrac{C}{2}.\tan \dfrac{A}{2})^3}$(2)
Từ (1),(2)
${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge \dfrac{1}{9}$

Dấu = khi $A = B = C$
Vậy tam giác ABC đều!
P/s: Kí hiệu Xích ma và suy ra bị hỏng, gõ mệt quá. Hơi rối mắt, sorry mọi người ...)

Làm gì mà khiếp ghê . Có cách dễ hơn nè: Áp dụng được cho bài tổng quát luôn :
$ tan^6\dfrac{A}{2} +\dfrac{1}{27}+\dfrac{1}{27} \geq \dfrac{1}{3}Tan^2\dfrac{A}{2} $
Làm tương tự với $ Tan^6\dfrac{B}{2}; Tan^6\dfrac{C}{2} $ Rồi cộng các Bdt lại ta được :
${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge \dfrac{1}{3}\sum tan^2\dfrac{A}{2}-\dfrac{2}{9} \geq \dfrac{1}{9} $

[vietfrog]

Làm gì mà khiếp ghê . Có cách dễ hơn nè: Áp dụng được cho bài tổng quát luôn :
$ tan^6\dfrac{A}{2} +\dfrac{1}{27}+\dfrac{1}{27} \geq \dfrac{1}{3}Tan^2\dfrac{A}{2} $
Làm tương tự với $ Tan^6\dfrac{B}{2}; Tan^6\dfrac{C}{2} $ Rồi cộng các Bdt lại ta được :
${\tan ^6}\dfrac{A}{2} + {\tan ^6}\dfrac{B}{2} + {\tan ^6}\dfrac{C}{2} \ge \dfrac{1}{3}\sum tan^2\dfrac{A}{2}-\dfrac{2}{9} \geq \dfrac{1}{9} $

Tôi phục ông quá. Xấu hổ quá. Hay!

[caubeyeutoan2302]

Đây là cách của đàn em nhỏ
Thật vậy ta dễ dàng chứng minh Đẳng thức lượng giác sau:
$ \sum{tan\dfrac{A}{2}.tan\dfrac{B}{2}=1$
Do đó ta dễ dàng chứng minh được:
$ (tan\dfrac{A}{2}+tan\dfrac{B}{2}+tan\dfrac{C}{2})^2 \ge 3(\sum{tan\dfrac{A}{2}.tan\dfrac{B}{2})=3$
Mặt khác áp dụng Holder ta có:
$3^{2n-1}.(tan^{2n}\dfrac{A}{2}+tan^{2n}\dfrac{B}{2}+tan^{2n}\dfrac{C}{2}) \ge (\sum{tan\dfrac{A}{2}})^{2n} \ge 3^{n}$
Từ đó suy ra :
$tan^{2n}\dfrac{A}{2}+tan^{2n}\dfrac{B}{2}+tan^{2n}\dfrac{C}{2} \ge \dfrac{3^{n}}{3^{2n-1}}=\dfrac{1}{3^{n-1}}$
Dấu bằng xảy ra khi A=B=C
Với cách suy luận , ta có thể tìm thêm vài BĐT đẹp nữa là:
$tan^{n}A+tan^{n}B+tan^{n}C \ge 3\sqrt{3^{n}}$
$cot^{2n}A+cot^{2n}B+cot^{2n}C \ge 3^{1-n}$
Câu 2 có vẻ hơi cầu kì nhỉ , em gợi ý, ta chứng minh BĐT sau:
Với x,y,z là 3 số dương ta sẽ có$x^{x}.y^{y}.z^{z} \ge (xyz)^{\dfrac{x+y+z}{3}}$
Cám ơn cách làm của các anh đóng góp , nhất là cách anh vietfrog , ấn tượng thật , hihi

[vietfrog]

Cám ơn cách làm của các anh đóng góp , nhất là cách anh vietfrog , ấn tượng thật , hihi

Huhu. Anh em ơi câubeyeutoan trêu tui ( . Ấn tượng mới đau chứ.
Xin góp vài bài nhân dạng tam giác xem ai giải ''ấn tượng'' hơn.
Bài 1: ( *)
Nhận dạng tam giác ABC biết :
${a^2} + {b^2} + {c^2} = 36{r^2}$
Với a,b,c là 3 cạnh; r là bán kính đường tròn nội tiếp.
Bài 2: (**)
Nhận dạng tam giác ABC biết:
$\sqrt {\tan A} + \sqrt {\tan B} + \sqrt {\tan C} = \sqrt {\cot \dfrac{A}{2}} + \sqrt {\cot \dfrac{B}{2}} + \sqrt {\cot \dfrac{C}{2}} $
Trong đó A,B,C là ba góc tam giác.
Bài 3:(***)
Tam giác ABC có tính chất gì nếu :
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$
Bài 4:(***)
Tam giác ABC có tính chất gì nếu :
${a^3} + {b^3} = {c^3}$
với a,b,c là các cạnh.
p/s : đừng giải ấn tượng giống tui nha (

Bài viết đã được chỉnh sửa nội dung bởi vietfrog: 18-07-2011 - 11:22

[Nguyễn Hoàng Lâm]

Bài 1: Giải phương trình:
$(2cos\dfrac{\pi}{7}-\dfrac{1}{2cos\dfrac{\pi}{7}})^{x}=1+(4cos^2\dfrac{\pi}{7}-3)^{x}$
Bài 2: Chứng minh rằng trong tam giác nhọn ABC, ta luôn có:
$ (tanA)^{tanA}.(tanB)^{tanB}.(tanC)^{tanC} \ge (\sqrt{3})^{3\sqrt{3}}$
Bài 3:
Cho tam giác ABC là tam giác nhọn , hãy xác định dạng của tam giác biết rằng:
$tan^6\dfrac{A}{2}+tan^6\dfrac{B}{2}+tan^6\dfrac{C}{2}=\dfrac{1}{9}$

bài 2 :
giả sủ $ x \geq y \geq z >0 $ đâu tiên ta sẽ chứng minh:

$ x^xy^y\geq (xy)^{\dfrac{x+y}{2}} $ giả sủ $ x\geq y $
BĐt tương đương với :
$ x^{\dfrac{x-y}{2}}.y^{\dfrac{y-x}{2}} \geq 1 \Leftrightarrow (\dfrac{x}{y})^{\dfrac{x-y}{2}}\geq 1 $
do $ x \geq y$ nên bđt trên đúng .
Áp dụng bđt trên ta có
Vậy ta cần cm thêm $ (xy)^\dfrac{x+y}{2}z^z\geq (xyz)^{\dfrac{x+y+z}{3}} $
$ \Leftrightarrow (xy)^{\dfrac{x+y-2z}{6}}.z^{\dfrac{2z-y-x}{3}} \geq 1 $
$ \Leftrightarrow (\dfrac{xy}{z^2})^{\dfrac{x+y-2z}{6}}\geq 1 $
Do $ x \geq y \geq z $ nên Bđt trên đúng . Đến đây chỉ việc áp dụng vào giải thui

[tolaphuy10a1lhp]

Bài 2: (**)
Nhận dạng tam giác ABC biết:
$\sqrt {\tan A} + \sqrt {\tan B} + \sqrt {\tan C} = \sqrt {\cot \dfrac{A}{2}} + \sqrt {\cot \dfrac{B}{2}} + \sqrt {\cot \dfrac{C}{2}} $
Trong đó A,B,C là ba góc tam giác.

Thử sức bài 2:
Chứng minh và áp dụng bất đẳng thức (1)

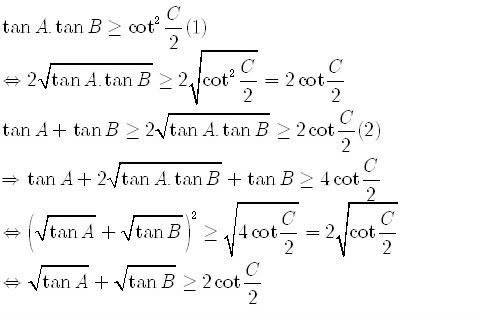
Dấu "=" của (1) và (2) xảy ra đồng thời $ \Leftrightarrow A = B $
Chứng minh tương tự :
$ \sqrt{tanB} + \sqrt{tanC} \geq 2 \sqrt{cot \dfrac{A}{2} } $
$ \sqrt{tanC} + \sqrt{tanA} \geq 2 \sqrt{cot \dfrac{B}{2} } $
Cộng vế theo vế $ \sqrt{tanA} + \sqrt{tanB} + \sqrt{tanC} \geq \sqrt{cot \dfrac{A}{2} } + \sqrt{cot \dfrac{B}{2}} +\sqrt{cot \dfrac{C}{2} } $
Dấu "=" xảy ra $ \Leftrightarrow A = B = C $ $ \Leftrightarrow \vartriangle ABC $ đều

[tiger_cat]

Bài 4:(***)
Tam giác ABC có tính chất gì nếu :
${a^3} + {b^3} = {c^3}$

Mình làm thế này ko bik có ổn ko.Cách ko hay mà dài

Để ý rằng $c>a$ và $c>b$ nên góc C lớn nhất trong tam giác

Đầu tiên chứng minh ${a^2} + {b^2} - {c^2} > 6(c - a)(c - b)$
CÁi này biến đổi tương đương thôi

$\{a^2} + {b^2} - {c^2} > 6(c - a)(c - b) $
$\Leftrightarrow {a^2}c + {b^2}c - {c^3} > 6c(c - a)(c - b) $
$\Leftrightarrow {a^2}(c - a) + {b^2}(c - b) > 6c(c - a)(c - b)$
$ \Leftrightarrow \dfrac{{{a^2}}}{{c - b}} + \dfrac{{{b^2}}}{{c - a}} > 6c$
Mà $\left\{ \begin{array}{l} {a^2} = \dfrac{{{a^3}}}{a} = \dfrac{{{c^3} - {b^3}}}{a} = \dfrac{{(c - b)({c^2} + bc + {b^2})}}{a} \\ {b^2} = \dfrac{{{b^3}}}{b} = \dfrac{{{c^3} - {a^3}}}{b} = \dfrac{{(c - a)({c^2} + ac + {a^2})}}{b} \\ \end{array} \right.$
Thay vào bdt ta có
$\dfrac{{{b^2} + bc + {c^2}}}{a} + \dfrac{{{c^2} + ac + {a^2}}}{b} > 6c \Leftrightarrow \left( {{a^3} + b{c^2} + {b^2}c} \right) + \left( {{b^3} + {a^2}c + a{c^2}} \right) > 6abc$
Áp dụng cô si 3 số thì thấy luôn đúng

Vậy ${a^2} + {b^2} - {c^2} > 6(c - a)(c - b)>0$ (do c>a và b>a)

Cơ mà $cosC= \dfrac{a^2+b^2-c^2}{2ab} $

Đâm ra $cosC>0$ =>góc C nhọn
Vậy góc A và góc B cũng nhọn luôn

Vì thế đáp án là tam giác nhọn $_$

Bài viết đã được chỉnh sửa nội dung bởi tiger_cat: 18-07-2011 - 20:50

[vietfrog]

Xin giới thiệu Tiger_cat , người bạn của tôi.
Cách giải như vậy là ổn rồi. Thêm một cách khác như thế này :
Ta có:
$\begin{array}{l} {({a^2} + {b^2})^3} = {a^6} + {b^6} + 3{a^2}{b^2}({a^2} + {b^2}) \\ \Rightarrow {({a^2} + {b^2})^3} \ge {a^6} + {b^6} + 3{a^2}{b^2}.2ab > {a^6} + {b^6} + 2{a^3}{b^3} \\ \Rightarrow {({a^2} + {b^2})^3} > {({a^3} + {b^3})^2} = {({c^3})^2} = {({c^2})^3} \\ \Rightarrow {a^2} + {b^2} > {c^2} \Rightarrow \cos C > 0 \\ \\ \end{array}$
Suy ra góc C nhọn. Từ giả thiết thấy góc C là góc lớn nhất.
Vậy Tam giác ABC nhọn!

[tiger_cat]

Bài 1: ( *)
Nhận dạng tam giác ABC biết :
${a^2} + {b^2} + {c^2} = 36{r^2}$
Với a,b,c là 3 cạnh; r là bán kính đường tròn nội tiếp.

Tiếp nhé

BĐT $<=>p^2(a^2+b^2+c^2)=36(rp)^2=36S^2$

$<=>p^2(a^2+b^2+c^2)=36p(p-a)(p-b)(p-c)$

$<=>p(a^2+b^2+c^2)=36(p-a)(p-b)(p-c)$

Nhận thấy $p(a^2+b^2+c^2)= \dfrac{a+b+c}{2}.(a^2+b^2+c^2) \geq \dfrac{(a+b+c)^3}{6} $

$36(p-a)(p-b)(p-c)=36. \dfrac{(a+b-c)(a+c-b)(b+c-a)}{8} \leq 36.\dfrac{(a+b-c+a+c-b+b+c-a)^3}{8.27} = \dfrac{(a+b+c)^3}{6}$

$=>VP=VP <=>a=b=c$ hay tam giác ABC đều

Bài viết đã được chỉnh sửa nội dung bởi tiger_cat: 18-07-2011 - 22:23

[tolaphuy10a1lhp]

Bài 3:(***)
Tam giác ABC có tính chất gì nếu :
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$

Cảm ơn Tú và bạn tiger_cat, mình giải lại bài này:
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$

$ \Leftrightarrow 2cos^{2} \dfrac{A}{2} .2cos^{2} \dfrac{B}{2} . 2cos^{2} \dfrac{C}{2} > 2 $
$ cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} > \dfrac{1}{2} $
$ 1 - 2 cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} <0 $
$ 1 - cos \dfrac{A}{2}(cos\dfrac{B - C}{2} - cos \dfrac{A}{2}) <0$
$ 1 - cos \dfrac{A}{2}.cos\dfrac{B - C}{2} + cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B - C}{2} - cos^{2} \dfrac{B - C}{2}<0$

$ sin^{2} \dfrac{B - C}{2}+ (cos\dfrac{B - C}{2} - cos \dfrac{A}{2})^{2} + \dfrac{3}{4} cos ^{2}\dfrac{A}{2} <0 $ (vô lý)

Dấu " =" ???

Bài viết đã được chỉnh sửa nội dung bởi tolaphuy10a1lhp: 19-07-2011 - 21:00

[tiger_cat]

Bạn xem bài 3, mình không biết đúng sai?
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$

$ \Leftrightarrow 2cos^{2} \dfrac{A}{2} .2cos^{2} \dfrac{B}{2} . 2cos^{2} \dfrac{C}{2} > 2 $
$ \Leftrightarrow cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} > \dfrac{1}{2} $
$ \Leftrightarrow 1 - 2 cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} < 0 $

Chứng minh được: $ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} = 1- 2cosAcosBcosC $

$ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} < 0 $
Vậy đề bài có dấu "=" không?; cách giải trên có được không??

Bài viết đã được chỉnh sửa nội dung bởi tiger_cat: 19-07-2011 - 09:54

[tiger_cat]

$ \Leftrightarrow 1 - 2 cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} < 0 $

Chứng minh được: $ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} = 1- 2cosAcosBcosC $

$ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} < 0 $

hê.Mấy cái dòng này đâu liên quan tới nhau

Bài viết đã được chỉnh sửa nội dung bởi tiger_cat: 19-07-2011 - 10:05

[caubeyeutoan2302]

Bạn xem bài 3, mình không biết đúng sai?
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$

$ \Leftrightarrow 2cos^{2} \dfrac{A}{2} .2cos^{2} \dfrac{B}{2} . 2cos^{2} \dfrac{C}{2} > 2 $
$ \Leftrightarrow cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} > \dfrac{1}{2} $
$ \Leftrightarrow 1 - 2 cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} < 0 $

Chứng minh được: $ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} = 1- 2cosAcosBcosC $

$ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} < 0 $
Vậy đề bài có dấu "=" không?; cách giải trên có được không??

Theo như mình biết chỉ có công thức :$cos^2A+cos^2B+cos^2C+2cosAcosBcosC=1$.
Còn công thức : $ cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B}{2} + cos^{2} \dfrac{C}{2} = 1- 2cosAcosBcosC $ , mình nghĩ có vẻ không ổn lắm .

[caubeyeutoan2302]

Cám ơn tất cả các bạn vì những lời giải hay . Tiếp theo là một vài bài toán tính toán lượng giác hơi khó một chút , mong các bạn sẽ tìm tòi và học hỏi được nhiều điều hay từ những bài này:
Bài 1:Cho
$P=(1+tan^0)(1+tan2^0)(1+tan3^0).........(1+tan45^0)=2^{n}$ . Hãy tìm giá trị của n
Bài 2: Hãy chứng minh rằng trung bình cộng của các số $ 2sin2^0, 4sin4^0, 6sin6^0,........,180sin180^0$ sẽ bằng với $cot1^0$

[tiger_cat]

Cảm ơn Tú và bạn tiger_cat, mình giải lại bài này:
$(1 + \cos A)(1 + \cos B)(1 + \cos C) > 2$

$ \Leftrightarrow 2cos^{2} \dfrac{A}{2} .2cos^{2} \dfrac{B}{2} . 2cos^{2} \dfrac{C}{2} > 2 $
: hai trường hợp :
* TH 1: $ cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} > \dfrac{1}{2} $
* TH 2: $ cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} < - \dfrac{1}{2} $

TH 1: $ cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} > \dfrac{1}{2} $
$ 1 - 2 cos\dfrac{A}{2} cos \dfrac{B}{2} cos \dfrac{C}{2} <0 $
$ 1 - cos \dfrac{A}{2}(cos\dfrac{B - C}{2} - cos \dfrac{A}{2}) <0$
$ 1 - cos \dfrac{A}{2}.cos\dfrac{B - C}{2} + cos^{2} \dfrac{A}{2} + cos^{2} \dfrac{B - C}{2} - cos^{2} \dfrac{B - C}{2}<0$

$ sin^{2} \dfrac{B - C}{2}+ (cos\dfrac{B - C}{2} - cos \dfrac{A}{2})^{2} + \dfrac{3}{4} cos ^{2}\dfrac{A}{2} <0 $ (vô lý)

* TH2 $ sin^{2} \dfrac{B - C}{2}+ (cos\dfrac{B - C}{2} + cos \dfrac{A}{2})^{2} + \dfrac{3}{4} cos ^{2}\dfrac{A}{2} >0 $ (Đúng)
Dấu " =" ???

Ko cần xét TH 2 nhé.Vì các giá trị cos đều ko âm

[spiderandmoon]

Cám ơn tất cả các bạn vì những lời giải hay . Tiếp theo là một vài bài toán tính toán lượng giác hơi khó một chút , mong các bạn sẽ tìm tòi và học hỏi được nhiều điều hay từ những bài này:
Bài 1:Cho
$P=(1+tan1^0)(1+tan2^0)(1+tan3^0).........(1+tan45^0)=2^{n}$ . Hãy tìm giá trị của n

Mình làm bài một nhé!!!!!!!!!
Với bài này ta chia P thành 22 nhóm có dạng $(1+tan \alpha )(1+tan(45^0 - \alpha )$ và một hạng tử $(1+tan45^0)(=2)$
Ta cần cm $(1+tan \alpha )(1+tan(45^0 - \alpha )=2$ (1)
Thật vậy, khi khai triển hết nhân tử ra ta sẽ có:
$VT= 1 + tan \alpha + tan(45^0- \alpha ) + tan \alpha .tan(45^0- \alpha )$
$= 1+ \dfrac{sin(\alpha + 45^0 - \alpha) }{cos \alpha .cos(45^0- \alpha )} + \dfrac{sin \alpha .sin(45^0 - \alpha )}{cos \alpha .cos(45^0- \alpha )}$
$= 1+ \dfrac{sin45^0 + sin \alpha .sin(45^0 - \alpha )}{cos \alpha .cos(45^0- \alpha )} $
$=1+ \dfrac{cos45^0 + \dfrac{1}{2} (cos(2 \alpha -45^0) - cos45^0)}{ \dfrac{1}{2} .(cos(2 \alpha -45^0) + cos45^0)} $
= 2
Rồi!!!!
Thế vào trong P ta sẽ được n= 23

Bài viết đã được chỉnh sửa nội dung bởi spiderandmoon: 20-07-2011 - 16:39

[caubeyeutoan2302]

Mình làm bài một nhé!!!!!!!!!
Với bài này ta chia P thành 22 nhóm có dạng $(1+tan )(1+tan(45^0 - \alpha )$ và một hạng tử $(1+tan45^0)(=2)$
Ta cần cm $(1+tan \alpha )(1+tan(45^0 - \alpha )=2$ (1)
Thật vậy, khi khai triển hết nhân tử ra ta sẽ có:
$VT= 1 + tan \alpha + tan(45^0- \alpha ) + tan \alpha .tan(45^0- \alpha )$
$= 1+ \dfrac{sin(\alpha + 45^0 - \alpha) }{cos \alpha .cos(45^0- \alpha )} + \dfrac{sin \alpha .sin(45^0 - \alpha )}{cos \alpha .cos(45^0- \alpha )}$
$= 1+ \dfrac{sin45^0 + sin \alpha .sin(45^0 - \alpha )}{cos \alpha .cos(45^0- \alpha )} $
$=1+ \dfrac{cos45^0 + \dfrac{1}{2} (cos(2 \alpha -45^0) - cos45^0)}{ \dfrac{1}{2} .(cos(2 \alpha -45^0) + cos45^0)} $
= 2
Rồi!!!!
Thế vào trong P ta sẽ được n= 23

Cám ơn spiderandmoon vì đánh giá đẹp của bạn, mình gợi ý bài tính giá trị trung bình nhé :
Các bạn hãy để ý công thức :$2.sin2k^0.sin1^0=cos(2k-1)^0-cos(2k+1)^0$