CMR: $AB^2 = CD.EF $

Hình 8
Bắt đầu bởi Rayky, 10-08-2011 - 12:20
#1
 Đã gửi 10-08-2011 - 12:20
Đã gửi 10-08-2011 - 12:20

Cho hình thang ABCD (CD: Đáy lớn). AK // BC. BI // AD. BI  AC = {F}. AK
AC = {F}. AK 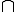 BD = {E}.
BD = {E}.
CMR: $AB^2 = CD.EF $
CMR: $AB^2 = CD.EF $
#2
 Đã gửi 10-08-2011 - 19:37
Đã gửi 10-08-2011 - 19:37

Giải:
Do AB song song với CD nên áp dụng hệ quả của định lý Tales, ta có:
Do BF song song với AD nên áp dụng định lý Tales, ta có:
Tương tự do AE song song với BC nên ta có:
Từ (1); (2); (3), suy ra:
Áp dụng định lý Tales đảo $ \Rightarrow EF // AB$
Do EF song song với AB nên $\dfrac{OF}{OA} = \dfrac{EF}{AB} (4)$
Từ (1); (3); (4), suy ra :

Do AB song song với CD nên áp dụng hệ quả của định lý Tales, ta có:
$ \dfrac{OA}{OC} = \dfrac{OB}{OD} = \dfrac{AB}{CD} (1)$
Do BF song song với AD nên áp dụng định lý Tales, ta có:
$\dfrac{OB}{OD} = \dfrac{OF}{OA} (2)$
Tương tự do AE song song với BC nên ta có:
$\dfrac{OA}{OC} = \dfrac{OE}{OB} (3)$
Từ (1); (2); (3), suy ra:
$\dfrac{OF}{OA} = \dfrac{OE}{OB}$
Áp dụng định lý Tales đảo $ \Rightarrow EF // AB$
Do EF song song với AB nên $\dfrac{OF}{OA} = \dfrac{EF}{AB} (4)$
Từ (1); (3); (4), suy ra :
$\dfrac{AB}{CD} = \dfrac{EF}{AB} \Rightarrow AB^2 = CD.EF$
Thế giới này trở nên bị tổn thương quá nhiều không phải bởi vì sự hung bạo của những kẻ xấu xa mà chính bởi vì sự im lặng của những người tử tế 
#3
 Đã gửi 10-08-2011 - 20:25
Đã gửi 10-08-2011 - 20:25

Cách CM EF // AB của bạn khác của mình, mà chắc chắn dùng nó CM nhanh hơn hẳn, cảm ơn bạn vì một cách hay nữa 
*Cách của mình:
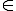 BI = {S}
BI = {S}
Ta có: AB // DI, AB // KC, AD // BI, AK // BC (gt)
 => ABID và ABCK là hình bình hành (dhnb)
=> ABID và ABCK là hình bình hành (dhnb)
 => AD = BI và AK = BC (t/c)
=> AD = BI và AK = BC (t/c)
Xét tam giác DAK và tam giác IBC, có:
AD = BI (cmt)
<DAK = <IBC (=<ASB)
AK = BC (cmt)
=> tam giác DAK = tam giác IBC (c.g.c)
=> DK = IC (cạnh tương ứng)
Xét tam giác ABE có AB // DK (gt)
Tá có: AB / DK = BE / DE (hệ quả Talet)
Xét tam giác ABF có AB // IC (gt)
Ta có: AB / IC = BF / IF (hệ quả Talet)
Mà IC = DK (cmt)
=> BE / DE = BF / IF
Mà E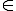 BD ; F
BD ; F 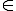 BI
BI
Nên EF // DI (đ/lý Talet đảo)
=> EF // CD => EF // AB
*Cách của mình:
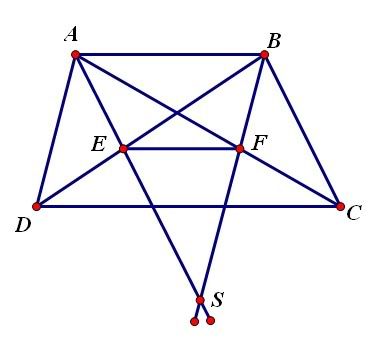
Ta có: AB // DI, AB // KC, AD // BI, AK // BC (gt)
Xét tam giác DAK và tam giác IBC, có:
AD = BI (cmt)
<DAK = <IBC (=<ASB)
AK = BC (cmt)
=> tam giác DAK = tam giác IBC (c.g.c)
=> DK = IC (cạnh tương ứng)
Xét tam giác ABE có AB // DK (gt)
Tá có: AB / DK = BE / DE (hệ quả Talet)
Xét tam giác ABF có AB // IC (gt)
Ta có: AB / IC = BF / IF (hệ quả Talet)
Mà IC = DK (cmt)
=> BE / DE = BF / IF
Mà E
Nên EF // DI (đ/lý Talet đảo)
=> EF // CD => EF // AB
Bài viết đã được chỉnh sửa nội dung bởi Rayky: 11-08-2011 - 14:01
0 người đang xem chủ đề
0 thành viên, 0 khách, 0 thành viên ẩn danh




