Chủ đề này có 20 trả lời

[Rayky]

Tình hình là mình cũng sắp thi lên cấp 3 và cũng có khá nhiều tài liệu toán hình hay và muốn chia sẽ, thảo luận với các bạn nên mình lập topic này. Mình sẽ cố gắng 1 ngày post 2 bài. Mọi người cố gắng đưa ra được càng nhiều cách càng tốt nhé. Cuối ngày mình sẽ đưa ra cách giải của mình hoặc cách giải chuẩn (nếu mình có và chưa bị trùng). Cuối cùng mình sẽ copy lại cách làm + hình vẽ của mọi người và mình rồi lưu lại dưới đề bài thành một tài liệu cho mọi người cùng tham khảo nếu cần

16/8/2011
Bài 1: Từ Chuyên đề Định lí Ceva và định lí Menelaus (Lớp 8)
Cho hình bình hành ABCD. Lấy điểm M trên cạnh AD sao cho AM = 2MD. Điểm N trên cạnh DC sao cho DN = 3NC. Hai đường thẳng BM và AN cắt nhau tại S. Tính tỉ số AS/SN.

Bài 2: Từ đề thi học sinh giỏi quốc tế (không rõ năm)
Cho tam giác ABC với các yếu tố độ dài các cạnh là: BC = a, AC = b, AB = c. CMR:
${a^2} + {b^2} + {c^2} \ge 4S\sqrt 3 $
(S ở đây là diện tích tam giác ABC)

Bài giải 16/8/2011

Mong mọi người ủng hộ

Bài viết đã được chỉnh sửa nội dung bởi Rayky: 17-08-2011 - 23:17

[Rayky]

Bài giải 16/8/2011
Bài 1: Theo cách của Perfectstrong

Trên AN lấy F sao cho MF//DC.
Ta có:
$\dfrac{MF}{DN}=\dfrac{MA}{DA}=\dfrac{2}{3}$
$\Rightarrow MF=\dfrac{2}{3}DN=\dfrac{2}{3}.\dfrac{3}{4}DC=\dfrac{1}{2}DC=\dfrac{1}{2}AB$
$\Rightarrow \dfrac{1}{2}=\dfrac{MF}{AB}=\dfrac{SF}{SA}$
$\Rightarrow \dfrac{AS}{AF}=\dfrac{2}{3}$
$\Rightarrow \dfrac{AS}{AN}=\dfrac{AS}{AF}.\dfrac{AF}{AN}=\dfrac{2}{3}.\dfrac{2}{3}=\dfrac{4}{9}$
$\Rightarrow \dfrac{AS}{SN}=\dfrac{4}{5}$

Bài 2:
C1: Theo cách của truclamyentu
$\begin{array}{l}4\sqrt 3 S = \sqrt {3(a + b + c)(a + b - c)(a + c - b)(b + c - a)} \le \sqrt {3(a + b + c)abc} \\\\\le \sqrt {{{(ab + bc + ca)}^2}} = ab + bc + ca \le {a^2} + {b^2} + {c^2}\end{array}$
Xảy ra đẳng thức tại a = b = c tam giác ABC đều.

C2:
Theo hệ quả Bất đẳng thức Bunhiacopski, ta có:
$\dfrac{1}{3}{(a + b + c)^2} \le {a^2} + {b^2} + {c^2}$ (1)
Áp dụng Bất đẳng thức Cauchy, ta có:
$\sqrt {p{{\left[ {\dfrac{{(p - a) + (p - b) + (p - c)}}{3}} \right]}^3}} \ge \sqrt {p(p - a)(p - b)(p - c)} $
$\dfrac{{{p^2}}}{{3\sqrt 3 }} \ge S$ (công thức Hê-rông)
$\dfrac{1}{3}.\dfrac{{{{(a + b + c)}^2}}}{{4\sqrt 3 }} \ge S$
Áp dụng (1) $S \le \dfrac{{{a^2} + {b^2} + {c^2}}}{{4\sqrt 3 }}$
$4\sqrt 3 S \le {a^2} + {b^2} + {c^2}$
Xảy ra đẳng thức tại a = b = c tam giác ABC đều.

Bài viết đã được chỉnh sửa nội dung bởi Rayky: 17-08-2011 - 23:10

[perfectstrong]

Bài 1:

Trên AN lấy F sao cho MF//DC.
Ta có:
$\dfrac{MF}{DN}=\dfrac{MA}{DA}=\dfrac{2}{3}$
$\Rightarrow MF=\dfrac{2}{3}DN=\dfrac{2}{3}.\dfrac{3}{4}DC=\dfrac{1}{2}DC=\dfrac{1}{2}AB$
$\Rightarrow \dfrac{1}{2}=\dfrac{MF}{AB}=\dfrac{SF}{SA}$
$\Rightarrow \dfrac{AS}{AF}=\dfrac{2}{3}$
$\Rightarrow \dfrac{AS}{AN}=\dfrac{AS}{AF}.\dfrac{AF}{AN}=\dfrac{2}{3}.\dfrac{2}{3}=\dfrac{4}{9}$
$\Rightarrow \dfrac{AS}{SN}=\dfrac{4}{5}$

@Rayki: Bạn học lớp mấy vậy? Mà mình nghĩ nên mỗi ngày một bài thôi! Thế là đủ rồi. 2 là quá nhiều

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 18-08-2011 - 11:27

[truclamyentu]

Tình hình là mình cũng sắp thi lên cấp 3 và cũng có khá nhiều tài liệu toán hình hay và muốn chia sẽ, thảo luận với các bạn nên mình lập topic này. Mình sẽ cố gắng 1 ngày post 2 bài. Mọi người cố gắng đưa ra được càng nhiều cách càng tốt nhé. Cuối ngày mình sẽ đưa ra cách giải của mình hoặc cách giải chuẩn (nếu mình có và chưa bị trùng). Cuối cùng mình sẽ copy lại cách làm + hình vẽ của mọi người và mình rồi lưu lại dưới đề bài thành một tài liệu cho mọi người cùng tham khảo nếu cần

16/8/2011
Bài 1: Từ Chuyên đề Định lí Ceva và định lí Menelaus (Lớp 8)
Cho hình bình hành ABCD. Lấy điểm M trên cạnh AD sao cho AM = 2MD. Điểm N trên cạnh DC sao cho DN = 3NC. Hai đường thẳng BM và AN cắt nhau tại S. Tính tỉ số AS/SN.

Bài 2: Từ đề thi học sinh giỏi quốc tế (không rõ năm)
Cho tam giác ABC với các yếu tố độ dài các cạnh là: BC = a, AC = b, AB = c. CMR:
${a^2} + {b^2} + {c^2} \ge 4S\sqrt 3 $
(S ở đây là diện tích tam giác ABC)

Mong mọi người ủng hộ

2)

$\begin{array}{l}4\sqrt 3 S = \sqrt {3(a + b + c)(a + b - c)(a + c - b)(b + c - a)} \le \sqrt {3(a + b + c)abc} \\\\\le \sqrt {{{(ab + bc + ca)}^2}} = ab + bc + ca \le {a^2} + {b^2} + {c^2}\end{array}$

Bài viết đã được chỉnh sửa nội dung bởi truclamyentu: 17-08-2011 - 22:35

[Rayky]

@perfectstrong: Em năm nay lên lớp 9, còn về số bài thì chắc 1 với 2 thế nào cũng được, tùy hôm. Mà đề bài 3 của anh có đúng không vậy Có gì thành bài 4 nhé anh X_X
17/8/2011
Bài 3:
Chứng minh công thức Hê-rông cho tam giác ABC:
$S = \sqrt {p(p - a)(p - b)(p - c)} $

Bài viết đã được chỉnh sửa nội dung bởi Rayky: 17-08-2011 - 23:25

[isaac_newtons]

@perfectstrong: Em năm nay lên lớp 9, còn về số bài thì chắc 1 với 2 thế nào cũng được, tùy hôm. Mà đề bài 3 của anh có đúng không vậy Có gì thành bài 4 nhé anh X_X
17/8/2011
Bài 3:
Chứng minh công thức Hê-rông cho tam giác ABC:
$S = \sqrt {p(p - a)(p - b)(p - c)} $

ta có :
$ S= \dfrac{1}{2}bcsinA $
$ S^2= \dfrac{1}{4}b^2c^2(1-cos^2A)=\dfrac{1}{4}b^2c^2[1- \dfrac{(b^2+c^2-a^2)^2}{4b^2c^2}] $
$ = \dfrac{1}{16}(2bc + b^2+c^2-a^2)(2bc-b^2-c^2+a^2) = \dfrac{1}{16} [(b+c)^2-a^2][a^2-(b-c)^2]= \dfrac{a+b+c}{2} \dfrac{b+c-a}{2}\dfrac{a-b+c}{2}\dfrac{a+b-c}{2}=p(p-a)(p-b)(p-c) $
vậy $S = \sqrt {p(p - a)(p - b)(p - c)} $

Bài viết đã được chỉnh sửa nội dung bởi isaac_newtons: 18-08-2011 - 06:55

[perfectstrong]

Mình xin đóng góp 1 bài mở rộng của bài 1:
Bài 1.2:
Cho hình bình hành ABCD. Lấy M trên tia AD sao cho D nằm giữa A, M và AM=2AD. Lấy C trên tia DC sao cho C nằm giữa D, N và DN=3CN. Đường thẳng AN và BM cắt nhau ở S. Tính $\dfrac{SA}{SN}$

@Rayky: Mình đã sửa lại r�ồi. Xin lỗi nhé!

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 19-08-2011 - 12:15

[Rayky]

Bài giải ngày 17/8/2011
Bài 3: Theo cách của isaac_newtons
Ta có :
$ S= \dfrac{1}{2}bcsinA $
$ S^2= \dfrac{1}{4}b^2c^2(1-cos^2A)=\dfrac{1}{4}b^2c^2[1- \dfrac{(b^2+c^2-a^2)^2}{4b^2c^2}] $
$ = \dfrac{1}{16}(2bc + b^2+c^2-a^2)(2bc-b^2-c^2+a^2) = \dfrac{1}{16} [(b+c)^2-a^2][a^2-(b-c)^2]= \dfrac{a+b+c}{2} \dfrac{b+c-a}{2}\dfrac{a-b+c}{2}\dfrac{a+b-c}{2}=p(p-a)(p-b)(p-c) $
vậy $S = \sqrt {p(p - a)(p - b)(p - c)} $

Ngày 18/8/2011 và ngày 19/8/2011
Bài 4: Từ chuyên đề hệ thức tam giác thường
Cho tam giác ABC có ${l_a},{l_b},{l_c}$ là những phân giác trong tam giác ABC. CMR:
$\dfrac{2}{R} \le \dfrac{1}{{{l_a}}} + \dfrac{1}{{{l_b}}} + \dfrac{1}{{{l_c}}} \le \dfrac{1}{r}$

Bài 5: Từ chuyên đề hệ thức tam giác thường
Cho tam giác ABC với các yếu tố độ dài các cạnh là: BC = a, AC = b, AB = c. CMR:
$\forall x,y,z > 0$
$\dfrac{x}{{y + z}}{a^2} + \dfrac{y}{{x + z}}{b^2} + \dfrac{z}{{x + y}}{c^2} \ge 2S\sqrt 3 $
(S ở đây là diện tích tam giác ABC)

P/S: @anh perfectstrong, em vẫn thấy đề như vậy mà X_X Sao lại

Lấy C trên tia DC sao cho C nằm giữa D, N và DN=3CN

được nhỉ khi DC cố định >.>

[Cao Xuân Huy]

@perfectstrong: Em năm nay lên lớp 9, còn về số bài thì chắc 1 với 2 thế nào cũng được, tùy hôm. Mà đề bài 3 của anh có đúng không vậy Có gì thành bài 4 nhé anh X_X
17/8/2011
Bài 3:
Chứng minh công thức Hê-rông cho tam giác ABC:
$S = \sqrt {p(p - a)(p - b)(p - c)} $

Mình chứng minh công thức theo cách khác.

Không mất tính tổng quát, giả sử góc A là góc trong lớn nhất ABC.
Kẻ đường cao AH. Đặt BH=x thì HC=a-x.
Ta có:
$c^2 - x^2 = b^2 - (a - x)^2 ( = h^2 )$
Giải ra ta được:
$x = \dfrac{{- b^2 + c^2 + a^2 }}{{2a}}$
Ta có:
$h^2 = c^2 - x^2 = c^2 - \dfrac{{( - b^2 + c^2 + a^2 )^2 }}{{4a^2 }} = \dfrac{{4a^2 c^2 - ( - b^2 + c^2 + a^2 )^2 }}{{4a^2 }} = \dfrac{{(2ac - b^2 + c^2 + a^2 )(2ac + b^2 - c^2 - a^2 )}}{{4a^2 }} = \dfrac{{{\rm{[}}(a + c)^2 - b^2 {\rm{][}}b^2 - (a - c)^2 {\rm{]}}}}{{4a^2 }} = \dfrac{{(a + b + c)(a + c - b)(b - a + c)(b + a - c)}}{{4a^2 }}$
Vậy:
$S^2 = \dfrac{1}{4}a^2 h^2 = \dfrac{{(a + b + c)(a + b - c)(b + c - a)(a + c - b)}}{{16}} = \dfrac{{2p.2(p - c).2(p - a).2(p - b)}}{{16}} = p(p - a)(p - b)(p - c)$

suy ta ĐPCM

Bài viết đã được chỉnh sửa nội dung bởi Cao Xuân Huy: 19-08-2011 - 22:38

[Crystal]

Ngày 18/8/2011 và ngày 19/8/2011
Bài 5: Từ chuyên đề hệ thức tam giác thường
Cho tam giác ABC với các yếu tố độ dài các cạnh là: BC = a, AC = b, AB = c. CMR:
$\forall x,y,z > 0$
$\dfrac{x}{{y + z}}{a^2} + \dfrac{y}{{x + z}}{b^2} + \dfrac{z}{{x + y}}{c^2} \ge 2S\sqrt 3 $
(S ở đây là diện tích tam giác ABC)

[b]Giải:
Áp dụng BĐT Bunhiacopski, ta có:

$\left( {\dfrac{{a^2 }}{{y + z}} + \dfrac{{b^2 }}{{z + x}} + \dfrac{{c^2 }}{{x + y}}} \right)\left( {y + z + z + x + x + y} \right) \ge \left( {a + b + c} \right)^2 $

$\Rightarrow 2\left( {\dfrac{{a^2 }}{{y + z}} + \dfrac{{b^2 }}{{z + x}} + \dfrac{{c^2 }}{{x + y}}} \right)\left( {x + y + z} \right) \ge \left( {a + b + c} \right)^2 $

$\Rightarrow \dfrac{x}{{y + z}}a^2 + \dfrac{y}{{z + x}}b^2 + \dfrac{z}{{x + y}}c^2 \ge \dfrac{1}{2}\left[ {\left( {a + b + c} \right)^2 - 2\left( {a^2 + b^2 + c^2 } \right)} \right]\,\,(1)$

Ta cần chứng minh:

$\dfrac{1}{2}\left[ {\left( {a + b + c} \right)^2 - 2\left( {a^2 + b^2 + c^2 } \right)} \right] \ge 2S\sqrt 3 \,\,(2)$

$(2) \Leftrightarrow 2ab + 2bc + 2ca \ge a^2 + b^2 + c^2 + 4S\sqrt 3 \,\,\,\,(3)$

(3) đúng và dấu "=" xảy ra $\Leftrightarrow a = b = c$

Từ (1) và (3) suy ra đpcm.

Dấu "=" xảy ra khi và chỉ khi đồng thời có dấu bằng trong (1) và (3)

$\Leftrightarrow \left\{ \begin{array}{l}a = b = c \\ \dfrac{a}{{y + z}} = \dfrac{b}{{z + x}} = \dfrac{c}{{x + y}} \\ \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = b = c \\ x = y = z \\ \end{array} \right.$.

Vậy ABC là tam giác đều và x = y = z.

P/s: các bạn tự chứng minh BĐT (3) nhé, xem như đó là một bài tập.

[Cao Xuân Huy]

Đóng góp cho 1 bài
Bài 6:
(Đề thi tuyển sinh chuyên toán Lê Quý Đôn Đà Nẵng 2005)
Cho đtròn tâm O bán kính R và dây AB căng cung 120 độ. M là một điểm thuộc cung nhỏ AB. Tìm GTNN của $\dfrac{1}{{MA}} + \dfrac{1}{{MB}}$

Anh em chưa ai giải hả. Để mình gợi ý cho.
Dựng điểm C sao cho tam giác ABC là tam giác đều rồi giải tiếp

Đóng góp cho 1 bài
Bài 6:
(Đề thi tuyển sinh chuyên toán Lê Quý Đôn Đà Nẵng 2005)
Cho đtròn tâm O bán kính R và dây AB căng cung 120 độ. M là một điểm thuộc cung nhỏ AB. Tìm GTNN của $\dfrac{1}{{MA}} + \dfrac{1}{{MB}}$

Sao không ai vào giải bài này thế. Mình gợi ý tiếp này. Kẻ BD//AM (D (O)).
Tới đây chắc là ra

[perfectstrong]

Đóng góp cho 1 bài
Bài 6:
(Đề thi tuyển sinh chuyên toán Lê Quý Đôn Đà Nẵng 2005)
Cho đtròn tâm O bán kính R và dây AB căng cung 120 độ. M là một điểm thuộc cung nhỏ AB. Tìm GTNN của $\dfrac{1}{{MA}} + \dfrac{1}{{MB}}$

Anh em chưa ai giải hả. Để mình gợi ý cho.
Dựng điểm C sao cho tam giác ABC là tam giác đều rồi giải tiếp
Sao không ai vào giải bài này thế. Mình gợi ý tiếp này. Kẻ BD//AM (D (O)).
Tới đây chắc là ra

Bài này có thể giải bằng 2 cách nhưng hướng chung là tìm GTLN của MA+MB.
C1: Trên tia đối tia MB, lấy C sao cho MC=MA. Dễ thấy C thuộc 1 cung cố định. Từ đây dễ tìm GTLN của MA+MB.
C2: Lấy C là trung điểm cung lớn AB. Gọi R là bán kính của (O). Dễ thấy ABC đều.
Sử dụng 1 bài toán quen thuộc, ta có $MA+MB=MC \le 2R$
$\Rightarrow \dfrac{1}{{MA}} + \dfrac{1}{{MB}} \ge \dfrac{4}{MA+MB} \ge \dfrac{4}{2R}=\dfrac{2}{R}$
Đẳng thức khi M là trung điểm cung nhỏ AB.

[Cao Xuân Huy]

Anh em làm bài nữa đi.
Bài 7:Cho hình vuông ABCD, trên cạnh BC lấy điểm E, kéo dài DC về phía C một đoạn CF=CE. Bd cắt EF tại K, DE cắt BF tại H. Chứng minh A,H,K thẳng hàng.
Bài này thì chắc không khó lắm.

[perfectstrong]

Bài 7:

Sử dụng tgnt cho mạnh.
$\angle KDC=\angle KFD=45^o$ (do CEF vuông cân tại C)
nên KDC vuông cân tại K. Suy ra E là trực tâm DBC
$\Rightarrow \angle DHF=\angle DKF=90^o \Rightarrow DKHF:tgnt \Rightarrow \angle KHD=\angle KFD=45^o(1)$
$\angle BAD+\angle BHD=180^o \Rightarrow DABH:tgnt \Rightarrow \angle AHD=\angle ABD=45^o(2)$
Chú ý là K,H cùng thuộc nửa mặt phẳng bờ DH nên từ (1),(2) ta có đpcm.

[perfectstrong]

Ủng hộ tiếp 2 bài:
Bài 8:
Cho ABC nhọn, AB<AC, nội tiếp (O). Tiếp tuyến tại A và C cắt tiếp tuyến tại B thứ tự ở M và N. Hạ BP AC tại P.
CMR: PB là phân giác của góc MPN


Bài 9:
Cho hình thang ABCD nội tiếp (O) có đáy nhỏ AB, đáy lớn CD. M,N thứ tự là trung điểm CD, AB. Vẽ tia AP là tia đối tia AD. PN cắt DB tại Q. CMR: tâm đường tròn nội tiếp MPQ nằm trên đường cố định.

[javier]

Ủng hộ tiếp 2 bài:
Bài 8:
Cho ABC nhọn, AB<AC, nội tiếp (O). Tiếp tuyến tại A và C cắt tiếp tuyến tại B thứ tự ở M và N. Hạ BP AC tại P.
CMR: PB là phân giác của góc MPN

Bài 8

*Từ M,N lần lượt kẻ MD, NE vuông góc với AC.

*Ta có $ \angle MAD + \angle OAC = 90 độ $, $ \angle NCE + \angle OCE = 90độ $, mà $ \angle OAC = \angle OCA$ $ \angle MAD =\angle NCE $

$ \Rightarrow \vartriangle MDA \sim \vartrignle NEC (g.g)$

$\Rightarrow \dfrac{MD}{NE}= \dfrac{AM}{CN} $, mà AM=BM, CN=BN (t/c tiếp tuyến)

$\Rightarrow \dfrac{MD}{NE}= \dfrac{BM}{BN} $, lại có $ \dfrac{BM}{BN}= \dfrac{DP}{EP} $ (đ/l Thales trong hình thang MDEN)

$\Rightarrow \dfrac{MD}{NE}= \dfrac{DP}{EP} $

$\Rightarrow \vartriangle MDP \sim \vartriangle NEP (c.g.c) \Rightarrow ... \Rightarrow Q.E.D$

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 28-08-2011 - 11:59
Sửa latex-Up h“nh nhé bạn

[perfectstrong]

Bài 8: Cách 2:
(Mượn lại cái hình trên)



$\angle BCA=\angle MBA=\angle MOB \Rightarrow \vartriangle PCB \sim \vartriangle OBM(g.g)$
$\Rightarrow \dfrac{OB}{MB}=\dfrac{PC}{PB}(1)$
Tương tự, $\vartriangle PAB \sim \vartriangle BON(g.g) \Rightarrow \dfrac{BN}{OB}=\dfrac{PB}{PA}(2)$
Nhân (1) và (2) vế theo vế, ta có:
$\dfrac{BN}{BM}=\dfrac{PC}{PA}$
Chú ý BN=CN;BM=AM nên $\dfrac{CN}{AM}=\dfrac{PC}{PA} \Rightarrow \vartriangle PCN \sim \vartriangle PAM(c.g.c)$
$\Rightarrow .... \Rightarrow Q.E.D$

[perfectstrong]

Khơi dậy topic. Không biết chủ topic đi đâu nên mình sẽ thay bạn ấy cầm trịch.
Tiếp tục một chùm bài toán về cực trị hình học. Vui lòng khi trả lời bài nào thì ghi rõ số thứ tự bài đó.
Bài 10:
Cho nửa đtròn (O) đường kính AB. Lấy C trên (O). Hạ CH AB. Vẽ hình chữ nhật CHBK. Xác định C để $S_{CHBK}$ đạt max.
Bài 11:
Cho M là 1 điểm nằm trong $\vartriangle ABC$. Xác định M để:
a)$MA^2+MB^2+MC^2$ đạt min
b)$MA+MB+MC$ đạt min.
Bài 12:
Cho A nằm trong góc vuông xOy. Một đường thẳng qua A cắt Ox,Oy thứ tự tại M,N. Xác định M,N để:
a) $S_{OMN}$ đạt max.
b) $OM+ON$ đạt min.
c*) $P_{OMN}$ đạt max.
Bài 13:
Cho BC là dây cố định của (O) và A di động trên cung lớn BC. Xác định A để:
a)$P_{ABC}$ đạt max.
b)$S_{ABC}$ đạt max.
c)r đạt max với r là bán kính đường tròn nội tiếp $\vartriangle ABC$ và $\angle BAC=60^o$
Bài 14:
Cho đoạn thẳng BC cố định và điểm A bất kì. Xác định A sao cho $S_{ABC}$ đạt max nếu
a)$AB+AC=k$: không đổi.
b)$AB.AC=k^2$: không đổi.
Bài 15:
Cho A nằm trong góc vuông xOy. Vẽ góc vuông zAt sao cho Az cắt Ox tại B, At cắt Oy tại C. Xác định vị trí B,C để $S_{OBAC}$ đạt max,min.
Bài 16:
Cho $\vartriangle ABC$ với trọng tâm G. Đường thẳng d qua G cắt AB,AC tại P,Q tương ứng. Xác định d để AP+AQ đạt min.
Bài 17:
Cho hình vuông ABCD có M di động trên BC, N di động trên CD sao cho $\angle MAN=45^o$. Tìm M,N để
a)$S_{AMN}$ đạt max,min.
b)$S_{CMN}$ đạt max,min.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 26-11-2011 - 15:13

[perfectstrong]

Không rõ đề quá khó hay các bạn không chịu post nhỉ? Buồn quá
Mình giải một số bài và đưa ra gợi ý các bài còn lại. Các bạn tự giải tiếp nhé.
Bài 10:
Đặt $BH=x;AO=OB=R$
$\vartriangle ABC$ vuông tại C, đường cao CH nên $CH=\sqrt{AH.BH}=\sqrt{(2R-x)x}$
Ta có:
$$S_{CHBK}=CH.BK=\sqrt {\left( {2R - x} \right)x} .x = \sqrt {\left( {2R - x} \right).{x^3}} = 3\sqrt 3 \sqrt {\left( {2R - x} \right).{{\left( {\frac{x}{3}} \right)}^3}}$$
\[ \leqslant 3\sqrt 3 .\sqrt {{{\left( {\frac{{2R - x + \frac{x}{3} + \frac{x}{3} + \frac{x}{3}}}{4}} \right)}^4}} = 3\sqrt 3 .\frac{{{R^2}}}{4}\]
Đẳng thức xảy ra khi $2R-x=\dfrac{x}{3} \Leftrightarrow x=\dfrac{3}{2}R$.
Vậy $\max S_{CHBK}=\dfrac{3\sqrt{3}}{4}R^2 \Leftrightarrow $ C thuộc (O) sao cho $BH=\dfrac{3}{2}R$.
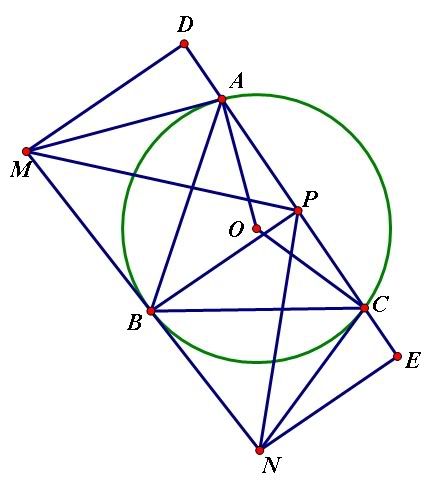
Bài 11:
a) Sử dụng pythagore kết hợp với BĐT B.C.S BT đạt min khi M là tâm đường tròn ngoại tiếp $\vartriangle ABC$
b) Điểm Torriceli :Vẽ phía ngoài $\vartriangle ABC$, $\vartriangle ADC$ đều. Sử dụng BĐT Ptoleme min của BT.
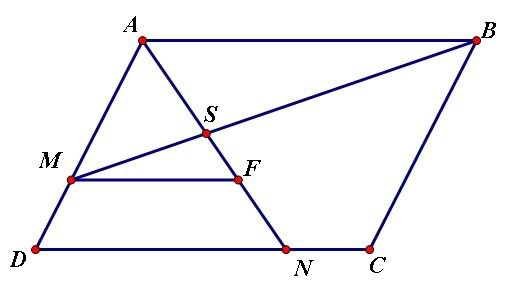
Bài 12:
a,b)Vẽ B,C thứ tự thuộc Ox,Oy sao cho $AB//Oy,AC//Ox \Rightarrow \dfrac{OB}{OM}+\dfrac{OC}{ON}=1$
c*)....
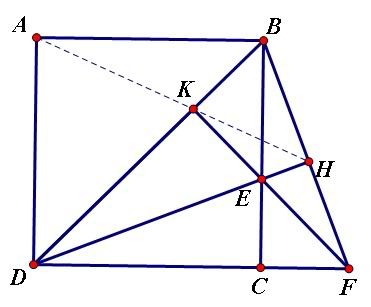
Bài 13:
a) Lấy D trên tia đối tia BA sao cho AD=AC. Chứng minh D thuộc đường cố định.
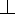
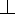
b) Hạ AH,OK BC. Hạ OL AH. $AH=AL+LH=AL+OK \leq OA+OK$
c)Đặt AB=x;AC=y. Dễ thấy $BC=R\sqrt{3}$. Chú ý:$S=pr=\dfrac{1}{2}xy.\sin BAC$
Bài 14:
Lưu ý: $\sin BAC \leq 1$. Đẳng thức xảy ra khi $\angle BAC=90^o$ và $S_{ABC}=\dfrac{1}{2}.AB.AC.\sin BAC$
Bài 15:
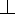
Hạ AD,AE Ox,Oy; đường thẳng qua A vuông góc với OA cắt Ox,Oy tại P,Q.
Bài 16:
Chú ý:$\dfrac{AB}{AP}+\dfrac{AC}{AQ}=3$
Bài 17:
a) Trên tia đối tia DC, lấy P sao cho DP=CN.
b) Đại số hóa. Đặt CM=x;CN=y.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 26-11-2011 - 15:21

[freeboyvnn]

Thay giup em bai nay nhe:

Bài 18:
Cho tam giac ABC co O la giao diem 2 đường phân giác góc A và B.
Kẻ OD, OE vuông góc lần lượt với AC và BC.
Gọi A1, B1 là hình chiếu của A và B trên OB và OA. Chứng minh: D, E, A1, B1 thẳng hang.


[email protected]

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 29-11-2011 - 21:47